López, F.A.,
Martínez, J.A. y Ruiz, M. (2013). Análisis espacial de lanzamientos en
baloncesto; el caso de L.A. Lakers / Spatial pattern analysis of shot attempts in basketball;the
case of L.A. Lakers. Revista Internacional de
Medicina y Ciencias de la Actividad Física y el Deporte vol. 13 (51) pp. 585-613. Http://cdeporte.rediris.es/revista/revista51/artanalisis409.htm
ORIGINAL
ANÁLISIS ESPACIAL
DE LANZAMIENTOS EN BALONCESTO; EL CASO DE L.A. LAKERS
SPATIAL PATTERN ANALYSIS OF SHOT ATTEMPTS IN BASKETBALL; THE CASE OF
L.A. LAKERS
López, F.A.1,
Martínez, J.A.2 y Ruiz, M.3
1 fernando.lopez@upct.es,
Profesor Titular. Departamento de Métodos Cuantitativos e Informáticos.
Universidad Politécnica de Cartagena. España
2
josean.martinez@upct.es, http://www.upct.es/~beside/jose , Profesor
Contratado Doctor. Departamento de Economía de la Empresa. Universidad
Politécnica de Cartagena. España
2 manuel.ruiz@upct.es, Profesor Titular.
Departamento de Métodos Cuantitativos e Informáticos. Universidad Politécnica
de Cartagena. España
Código
UNESCO / UNESCO Code: 5899 Educación Física y Deporte /
Physical Education and Sport
Clasificación Consejo
de Europa / Council of Europe Classification: 17 (Otras: Análisis cuantitativo del
deporte) / Other: Quantitative analysis of sport
Recibido 22 de julio
de 2011 / Received July 22, 2011
Aceptado 15 de diciembre
de 2011 / Accepted December 15, 2011
RESUMEN
La
importancia del análisis cuantitativo del deporte a través del uso de
estadísticas de juego ha sido un área de creciente interés en los últimos años.
En esta investigación mostramos una aplicación de la
estadística espacial al entendimiento del juego en baloncesto. Esta metodología
ha sido infrautilizada en la investigación en deporte hasta la fecha,
especialmente en baloncesto. Así, describimos una técnica de segmentación
espacial, como el test de Kulldroff, que es ampliamente utilizado en
epidemiología, y puede ser aplicado para analizar estadísticas de juego en
baloncesto. Este test detecta clusters de lanzamientos de baja y alta
incidencia, caracterizando mejor el juego de los equipos y de los jugadores.
Además, desarrollamos un test basado en entropía, el test V, que permite
comparar los mapas de lanzamiento. Para ilustrar empíricamente el atractivo de
esta aproximación metodológica, aplicamos estos análisis al rendimiento del
equipo de la NBA: Los Angeles Lakers. Este equipo vivió una enorme
transformación en las últimas temporadas, pasando de ser una franquicia de
rendimiento medio a ganar la NBA, debido a, entre otros factores, la
incorporación de dos jugadores clave en la temporada 2007-08: Pau Gasol y Derek
Fisher.
PALABRAS CLAVES: Baloncesto, clusters de lanzamientos,
análisis espacial, NBA.
ABSTRACT
The importance of quantitative
analysis in sports using objective data (such as game statistics), has been had
prominent in recent years. In this paper we have shown an application of
spatial statistics to understand more thoroughly the game of basketball. This
methodology has been rarely used in sports research, specifically in
basketball. We have depicted how a spatial clustering technique, such as the Kulldroff test, which is widely employed in epidemiology,
can be applied to analyze basketball data. This test detects low and high
incidence clusters of shots, and therefore it better characterizes the game of
teams and individual players. In addition, we have also used a test based on
entropy, the V-test, which serves to statistically compare shooting maps. We
illustrate the interesting contribution of this methodological perspective in
the case of the analysis of the Lakers’ performance, showing the transformation
of this team from a medium-level NBA franchise into a champion team, because
of, among other factors, the incorporation of two key players in the 2007-08 season: Pau Gasol and Derek
Fisher.
KEYWORDS:
Basketball, Cluster of shots, Spatial analysis,
NBA
1. INTRODUCCIÓN
La
importancia del análisis cuantitativo del deporte usando datos objetivos, como
los derivados de las estadísticas de juego, ha crecido ampliamente en los
últimos años. De hecho, la atención del mundo académico y profesional a este
tipo de análisis se ha incrementado exponencialmente desde la aparición del
fenómeno “Moneyball” (Lewis, 2003). En la disciplina específica del baloncesto,
la significación de esta línea de investigación es notable, y ha sido
protagonista de artículos en revistas académicas (ej, Berri, 1999; Berri y
Bradbury, 2010; Esteller-Moré y Eres-García, 2002; Kubatko,
Oliver, Pelton y Rosenbaum,
2007; Piette, Annand y Zang
2010), libros seminales (ej. Oliver, 2004; Winston, 2009), libros de predicción
(ej. Doolittle y Pelton, 2009; Hollinger, 2005), y un amalgama de webs
especializadas (ej. www.apbrmetrics.com, www.hoopsstats.com,
www.nbastuffer.com,
www.basketball-reference.com, www.82games.com,
www.basketballvalue.com).
Hay
tres principales líneas de investigación en baloncesto, en relación con la
aplicación del análisis cuantitativo de estadísticas de juego. La primera está
relacionada con la valoración del rendimiento de los equipos y de los
jugadores, con el fin de conseguir una visión más objetiva sobre la
productividad, eficacia, eficiencia y valor de los jugadores en el juego.
Algunos de los más destacados estudios sobre este tema son: Berri (1999; 2008),
Berri y Eschker (2005), Fernández, Camerino, Anguera y Jonsson (2009), Hoon-Lee
y Berri (2008), Esteller-Moré y Eres-García (2002), Mavridis,
Tsamourtzis, Karipidis y Laios (2009), Rimler, Song y Yi (2010), Piette, Annand y Zang (2010). La segunda está relacionada con la obtención
de predicciones ajustadas, con el objetivo de minimizar el riesgo de los
decisores (directivos, entrenadores, etc.). Algunos de los estudios más
relevantes sobre este tema son los siguientes: Alferink, Critchfield, Hitt y
Higgins (2009), Berri, Brook y Schmidt (2007), Berri y Schmidt (2002), Berry,
Reese y Larkey (1999), Hitt, Alferink, Critchfield y Wagman (2007), Romanowich,
Bourret y Vollmer (2007), Sánchez, Castellanos y Dopico (2007), Skinner (2010),
Tauer, Guenther y Rozek, (2009), Trininic, Dizdar y Luksic (2002), Vollmer y
Bourret (2000). Finalmente, una tercera corriente de investigación se ha
enfocado en análisis de temas controvertidos, como la manipulación de la
competición, determinación de salarios, discriminación racial, así como otros
diferentes tópicos como la existencia de rachas de juego o de lanzamiento. Una
muestra de esos estudios es: Arkes, (2010), Arkes y Martínez (2011), Bar-Eli, Avugos y Raab,
2006, Berri, Brook, Frick, Fenn y Vicente-Mayoral
(2005), Balsdon, Fong y
Thayer (2007), Fort, Hoon-Lee y Berri
(2008), Fort y Maxcy (2003), Gilovich,
Vallone y Tversky (1985), Humphreys (2000; 2002), Michaelides
(2010), Price y Wolfers (2010), Vergin
(2000), Zimmer y Kuethe
(2007).
Sin
embargo, muy pocos estudios han analizado el juego del baloncesto desde una
perspectiva espacial, más allá de las estadísticas básicas que aparecen en el
resumen del partido. La progresiva inclusión de las coordenadas de lanzamiento
en los datos jugada a jugada en las mejores competiciones del mundo (ver
Martínez, 2010) facilita este análisis usando estadística espacial. No
obstante, según hemos podido comprobar, sólo las investigaciones de Hickson y
Waller (2003) y Reich, Hodges, Carlin y Reich (2006) han usado esta
perspectiva. Ambos estudios sólo analizaban el rendimiento de un solo jugador
(Michael Jordan y Sam Cassell, respectivamente). Como Piette, Sathyanarayan y
Kai (2010) explican, el primer estudio modela cada lanzamiento como un evento
de un proceso de Poisson, y estima la correspondiente función no paramétrica en
relación con ese evento. El segundo estudio aplica un modelo logit multivariado
bayesiano a los datos espaciales, en conjunción con varias covariables. Para
determinar los parámetros del modelo, se realiza un muestreo por el método de
las cadenas de Markov en simulaciones Monte Carlo. Los resultados de esos dos
estudios son ejemplos valiosos de las posibilidades de este tipo de
aproximación metodológica.
Aunque
la estadística espacial está siendo progresivamente incorporada al análisis del
deporte (ej. Mulrooney, 2007) y existe una continua mejora en la generación de
los datos sobre coordenadas de lanzamiento en baloncesto (Chen, Tien, Chen,
Tsai y Lee, 2009), sigue siendo necesaria la utilización de una herramienta
potente para entender los patrones espaciales de lanzamiento, con el fin de
ayudar a los entrenadores y a los analistas a evaluar el juego, y así tomar
decisiones con menor riesgo. Además, esta aproximación puede complementar otras
investigaciones sobre dinámica espacio-temporal de coordinación de equipos de
baloncesto (Bourbousson, Sève y McGarry, 2010; Jäger y Schöllhorn, 2007), o
habilidades de tiro (Piette, Sathyanarayan y Kai, 2010). Por tanto, el
procedimiento que presentamos en este estudio es una aproximación novedosa para
enriquecer la información obtenida de los datos jugada a jugada de los partidos
de baloncesto, y de la monitorización y seguimiento en vídeo de los jugadores.
En
esta investigación usamos una perspectiva diferente a otros estudios para
analizar espacialmente los lanzamientos. Así, las contribuciones novedosas de
este estudio son las siguientes: en primer lugar, aplicamos nuestro análisis a
los lanzamientos intentados, tanto de los equipos como de los jugadores a nivel
individual. Específicamente, centramos nuestro análisis sobre Los Angeles
Lakers, equipo que compite en la NBA. De esta manera, somos capaces de detectar
diferencias en el patrón de lanzamiento entre los Lakers y el resto de la liga,
así como entre los propios jugadores del equipo californiano. En segundo lugar,
usamos el test de Kulldorff (Kulldorff, 1997) para analizar los datos
espaciales y detectar clusters de alta y baja incidencia en el lanzamiento, lo
que es una novedad en ciencias del deporte. Esta herramienta, permite encontrar
patrones de localización de tiro, y visualmente mostrar estas áreas, con el fin
de comparar intuitivamente el rendimiento de equipos y jugadores. Obviamente,
el enfoque estadístico de este proceso de clusterización provee mucha más
información relativa al rendimiento en los lanzamientos que el mero análisis
descriptivo de localización del tiro (como por ejemplo el análisis realizado en
webs especializadas como www.82games.com/shotzones.htm o http://hoopdata.com/shotstats.aspx). Como mostramos en nuestra
aplicación empírica, la utilidad del análisis espacial se ejemplifica en el
análisis de la transformación en el rendimiento sufrida por los Lakers, equipo
que pasó de ser una franquicia de rendimiento medio en la temporada 2006-07, a
ganar el título de la NBA en la temporada 2008-09, gracias a (entre otros
factores), la incorporación de dos jugadores clave en la temporada 2007-08: Pau
Gasol y Derek Fisher.
Por
tanto, en esta investigación damos respuestas a cuestiones como: ¿Tienen los
Lakers un patrón espacial de tiro diferente al resto de equipos de la NBA? O,
de forma similar, ¿tiene el jugador P un patrón espacial de tiro diferente del
resto de su equipo? Además, al analizar el patrón espacial de lanzamiento de un
jugador P, una cuestión interesante es: ¿Existe un cluster espacial de tiro de
alta frecuencia (baja frecuencia, respectivamente) de los Lakers o del jugador
P que difiere de lo que sería esperado por azar en relación con la población de
todos los lanzamientos de la NBA o de los equipos? Y es que al obtener los
clusters de lanzamiento de alta y baja frecuencia se está en disposición de
encontrar si la incorporación de un jugador P ha cambiado el patrón espacial de
lanzamiento de su equipo (o de otros jugadores de su equipo), al comparar el
cluster entre temporadas diferentes, es decir, la temporada de su incorporación
frente a la temporada anterior. En definitiva, el objetivo de esta
investigación es mostrar las posibilidades que tiene la aplicación de la
estadística espacial, y en este caso el test de Kulldorff (con el complemento
de un test de entropía), para analizar el patrón de lanzamientos de los
jugadores y equipos de baloncesto, con el fin de detectar cambios en los
patrones de tiro y comparar diferentes mapas de localización espacial, en aras
de detectar las zonas de alta y baja incidencia.
1.1.
LA
TRANSFORMACIÓN DE LOS LAKERS
En la
temporada 2006/07 los Lakers estaban viviendo un periodo de transición después de
5 años de éxitos (4 finales jugadas y 3 de ellas ganadas desde 2000 hasta
2004), y 2 años de fracasos (2004/05 y 2005/06). En esas dos últimas campañas
infructuosas los Lakers no se clasificaron para los play-offs en la primera de ellas, y fueron eliminados en la primera
ronda en la temporada siguiente. Por tanto, los Lakers comenzaron la temporada
2006/07 con importantes dudas relativas su rendimiento. Hay que destacar que la
franquicia californiana es una de las más laureadas de la historia de la NBA, y
sus expectativas de rendimiento siempre son muy exigentes. En esa temporada
2006/07, la primera de nuestro análisis, los Lakers rindieron peor que la
anterior campaña (porcentaje de victorias de 0,51 frente a 0,54), y también
fueron eliminados en primera ronda de play-offs.
La
siguiente temporada (2007/08) los Lakers realizaron importantes cambios en su
plantilla. Ficharon al base Derek Fisher el 20 julio de 2010, al alero Trevor
Ariza el 20 de noviembre de 2010, y ala-pivot Pau Gasol el 1 de febrero de 2008.
Estos fueron los movimientos de jugadores más relevantes en esa temporada,
porque otros jugadores que ficharon también por los Lakers tuvieron una
presencia marginal en la rotación (ver todos los movimientos de los jugadores y
sus estadísticas en www.basketball-reference.com). Por el contrario, uno de los
jugadores más notables en la anterior temporada, Smush Parker, firmó en julio
de 2007 como agente libre con Miami Heat, y otro jugador importante, como
Maurice Evans, fue vendido en la operación para conseguir el traspaso de Trevor
Ariza.
Finalmente,
en la temporada 2008/09 no hubieron cambios relevantes en la plantilla, porque
los pocos movimientos realizados tuvieron muy poco efecto en la distribución de
minutos por partido del resto de jugadores. En esas tres temporadas, Kobe
Bryant y Lamar Odom fueron siempre dos de los 3 jugadores con más minutos de
juego, por lo que pueden ser considerados como factores de referencia en el
rendimiento del equipo en ese lapso de tiempo analizado. Obviamente, es
pertinente recordar que Kobe Bryant es una de las máximas estrellas de la
competición, y es considerado como uno de los mejores jugadores en toda la
historia de la NBA.
Los
Lakers consiguieron un porcentaje de victorias del 51% en la temporada 2006/07,
69% en la 2007/08 y 79% en la 2008/09. En esas dos últimas temporadas los
Lakers jugaron la final de la NBA, ganando la última de ellas. La
transformación del rendimiento del equipo fue evidente, siendo la temporada
2007/08 el punto de inflexión de ese cambio. Los analistas especializados están
de acuerdo en que la incorporación de Fisher y Gasol fue crucial para la
transformación (ej.. Bresnahan, 2010; Kleeman, 2009;
Manning, 2009; Sanderson, 2010). Hay que remarcar, asimismo, que Ariza sólo
jugó 24 partidos en esa temporada, a causa de una lesión. Antes de firmar a
Gasol, los Lakers tenían record de victorias de 65% en los primeros 46 partidos
de la competición. Tras la incorporación de Gasol, y considerando sólo los 27
encuentros en los que el español jugó (se perdió 9 partidos por una lesión),
los Lakers consiguieron un registro de 84%.
En
esta investigación analizamos si este cambio tan evidente en el rendimiento de
los Lakers está reflejado en los diferentes patrones de localización de tiro, o
si la llegada de Gasol y Fisher cambió el juego de los Lakers desde el punto de
vista espacial, así como si jugadores como Bryant u Odom modificaron su modelo
de distribución espacial de lanzamientos.
Las
estadísticas básicas parcialmente reflejan esa transformación (Tabla 1). Los
Lakers mejoraron su eficiencia ofensiva y defensiva, pero los porcentajes de
tiros de campo y los lanzamientos libres fueron muy similares en las tres
temporadas (con una ligera mejora). Como los Lakers cogieron más rebotes,
robaron más balones y cometieron menos pérdidas, entonces pudieron lanzar con
más asiduidad, y por ende mejoraron los puntos por partido. Así, en la segunda
de las temporadas analizadas, los lanzamientos de campo intentados se
incrementaron en 2,89 por partido, y en la tercera temporada 1,98.
Consecuentemente, el juego ofensivo cambió de manera más notoria que el
defensivo.
Tabla 1. Estadísticas del box-score
de los Lakers y sus oponentes en esas tres temporadas regulares.
|
|
|
FGA |
FG% |
3PA |
3P% |
FTA |
FT% |
TRB |
AST |
STL |
BLK |
TOV |
PTS |
PTS/G |
W-L% |
|
2006/07* |
Lakers |
6581 |
0,466 |
1702 |
0,353 |
2193 |
0,747 |
3339 |
1827 |
593 |
416 |
1257 |
8368 |
102 |
0,512 |
|
|
Oponentes |
6635 |
0,461 |
1444 |
0,358 |
2291 |
0,76 |
3420 |
1776 |
641 |
404 |
1193 |
8374 |
102 |
|
|
2007/08 |
Lakers |
6818 |
0,476 |
1751 |
0,378 |
2270 |
0,769 |
3620 |
2003 |
654 |
438 |
1156 |
8904 |
108,6 |
0,695 |
|
|
Oponentes |
7022 |
0,445 |
1531 |
0,362 |
1995 |
0,752 |
3509 |
1793 |
634 |
368 |
1168 |
8309 |
101 |
|
|
2008/09 |
Lakers |
6981 |
0,474 |
1516 |
0,361 |
2087 |
0,77 |
3602 |
1908 |
718 |
420 |
1103 |
8768 |
106,9 |
0,793 |
|
|
Oponentes |
6825 |
0,447 |
1700 |
0,345 |
1931 |
0,753 |
3399 |
1854 |
635 |
392 |
1275 |
8140 |
99,3 |
|
FGA: Lanzamientos de campo intentados; FG%: Porcentaje de
acierto en tiros de campo; 3PA: Lanzamientos de tres puntos intentados; 3P%:
Porcentaje de acierto en lanzamientos de tres puntos; FTA: Tiros libres
intentados; FT%: Porcentaje de acierto en tiros libres; TRB: Rebotes totales;
AST: Asistencias; STL: Robos; BLK: Tapones; TOV: Pérdidas; PTS: Puntos; PTS/G:
Puntos por partido; W-L%:Porcentaje de victorias.
* Los Lakers jugaron 250 minutos extra en esta temporada
comparado con las dos temporadas siguientes, debido a las prórrogas. Por tanto,
hemos relativizado los datos de esa temporada, con el fin de que los números
sean comparables.
Fuente:
www.basketball-reference.com
Aunque
estas estadísticas son muy útiles para entender el cambio en el rendimiento de
los Lakers, mostraremos cómo la estadística espacial puede ser una herramienta
poderosa para complementar esa información proveniente de las estadísticas
básicas, ofreciendo nuevas perspectivas sobre cómo los Lakers cambiaron su
juego ofensivo y defensivo, a través de la modificación de su patrón de
localización espacial de lanzamiento.
2.
MÉTODOLOGÍA
Se dispone de información, jugada a jugada, de 3509
partidos jugados en la NBA en tres temporadas, 2006/07, 2007/08 y 2008/09. La
información se obtuvo de la pagina web www.basketballgeek.com. Esta es la única fuente de información gratuita que
aporta datos sobre la localización desde la que los jugadores realizaron los
lanzamientos. En total, en estas tres temporadas se celebraron 3690 partidos y
por tanto se asume una pérdida del 4,9% de los datos. Se ha realizado un
proceso de validación para confirmar que la pérdida de información no era
importante y asegurar que los lanzamientos a canasta codificados por www.basketballgeek.com y las estadísticas oficiales fueran coincidentes. En
este proceso de validación, encontramos una concordancia superior al 99% entre
la base de datos descargada y las estadísticas oficiales de los Lakers y
alrededor de un 95% con toda la NBA. Esto nos permite asegurar que la
información disponible en la base de datos tiene un elevado grado de fiabilidad
y que las pérdidas de información no son significativas y no afectarán a
nuestras conclusiones finales. Los datos fueros leídos y filtrados usando
MATLAB 2010b.
Para cada uno de estos 3509 partidos se dispone de
información exacta de las siguiente variables asociadas a cada una de las
jugadas que componen el partido: (i) minuto y segundo en el que se realizó la
jugada, (ii) equipo que realizó el intento de lanzamiento en dicha jugada (iii)
jugador que realizó el intento de lanzamiento en la jugada, (iv) coordenadas (x,y) de las localización del jugador cuando realizó el
intento de lanzamiento a canasta. En total se analizan 563740 jugadas en las
tres temporadas.
Para obtener la localización exacta, coordenadas (x,y) del lanzamiento, sobre toda la cancha se considera superpuesta
una retícula regular cuadrada donde cada celda tiene un tamaño aproximado de 30´30 cm2. Tendremos de esta
forma dividida la cancha en una retícula compuesta por 51 columnas (la coordenada
x puede tomar todos los valores enteros comprendidos entre 1 y 51) y 84 filas
(y=1,2,…,84). Consideraremos además que si el jugador se encuentra de pie
detrás del aro del equipo atacante entonces el eje X va de izquierda a derecha
y el eje Y va de abajo a arriba.
Aunque a lo largo de estas tres temporadas se han
realizado intentos de lanzamientos casi desde cualquier parte de la cancha,
centraremos nuestro análisis sólo en las celdas de esta retícula impuesta sobre
la cancha más próxima al aro donde se desarrolla la casi totalidad de los
lanzamientos, eliminando de esta forma tiros anecdóticos. Así, en lo que sigue,
sólo consideraremos aquellos lanzamientos que se han realizado justo antes de
la mitad de la cancha (y<36), excluyendo los más lejanos al aro y los
realizados en las dos líneas detrás de la canasta (y>2). Por tanto, sólo
consideraremos los lanzamientos donde ‘y’ puede variar entre 3 y 35. La
superficie de juego que analizaremos será una retícula que tiene un total de
R=51´33 = 1683
localizaciones.
2.1.
TEST
DE KULLDORFF
Para detectar clusters espaciales de alta o baja
incidencia en el número de intentos de lanzamientos utilizaremos el test de
Kulldorff. El procedimiento para este contraste es imponer una ventana sobre el
mapa y mover el centro de la ventana sobre cada localización de manera que la
ventana incluya conjuntos diferentes de puntos vecinos en diferentes
localizaciones. Ajustando la localización del centro y el radio de la ventana
el método genera un gran número de ventanas distintas, cada una de ellas
incluyendo diferentes conjuntos de puntos vecinos. En cada localización, el
tamaño de la ventana se aumenta continuamente desde '0' hasta un tamaño máximo
definido por el investigador. El parámetro “tamaño máximo” pone una cota superior
para el radio de la ventana en una de las dos formas siguientes: (1)
especificando un porcentaje máximo del total de la población dentro de la
ventana o (2) especificando el radio máximo del círculo. La opción (1) es la
que usaremos en este artículo. Debido a la forma de la cancha hemos utilizado
ventanas de forma elíptica con un tamaño máximo del 5% del total de
lanzamientos a canasta.
La
hipótesis nula en el contraste de Kulldorff es que en todas las localizaciones
la probabilidad de realizar un tiro a canasta es la misma mientras que la
hipótesis alternativa es que existe una ventana W tal que la probabilidad de
realizar un lanzamiento dentro de W es diferente de realizarlo fuera de W.
Ahora introducimos alguna notación que será necesaria para la descripción
matemática del contraste.
Sea n
el número total de lanzamientos a canasta del jugador P. Sean ns y nW
el número total de lanzamientos realizados por el jugador P en la
localización s y en la ventana W respectivamente. Sean Ns, NW
y N el número total de lanzamientos del equipo en la localización s, ventana W
y en toda la cancha respectivamente. Obsérvese que la variable Xs
que cuenta el número de lanzamientos realizados por el jugador P en la
localización s se distribuye como una distribución Binomial B(Ns,ps)
donde ps es la probabilidad de lanzamiento por el jugador P en la
localización s. Entonces la hipótesis nula y la alternativa pueden ser
contrastadas como
H0: 
para todo sÎS
H1: Existe una
ventana W tal que 
para todo sÎW y 
para todo 
con 
respectivamente.
Por
tanto bajo la hipótesis nula H0 la distribución conjunta de las R
variables 
sigue una distribución multinomial con función
de verosimilitud 
mientras
que bajo H1 la función de verosimilitud permanece como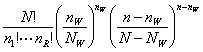 
.
Entonces el estadístico ratio de verosimilitud en la ventana W es:
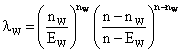donde 
es el valor esperado de lanzamientos en la
ventana W bajo H0.
Entonces
el estadístico de Kulldorff para alta y baja
frecuencia de lanzamientos se define como el máximo de los valores 
con W recorriendo todas las ventanas
posibles de la retícula S, es decir,
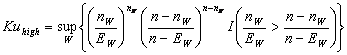
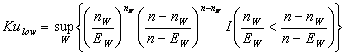
donde I(x) es una function indicador que
toma el valor 1 si la función logica x es cierta y 0 en otro caso. Para evaluar
la significación estadística del cluster principal, se genera un número
grande de réplicas del conjunto de datos bajo la hipótesis nula. El p-valor se
obtiene mediante contraste de hipótesis de Monte Carlo (Dwass
1957), comparando la posición de la máxima verosimilitud del conjunto real de
datos con la máxima verosimilitud de los datos simulados por Monte Carlo. Si la
posición es r, entonces el p-valor = r/(1 + #
simulaciones). Repitiendo este procedimiento y eliminando la ventana
seleccionada se puede detectar clusters secundarios. Existe software gratuito
para realizar el contraste de Kulldorff, SatScan, que se puede descargar de la
web www.satscan.org.
De manera similar y utilizando el contraste del ratio de
verosimilitud, podemos diseñar un contraste no paramétrico para detectar diferencias
globales en los patrones de la frecuencia de lanzamiento. Este estadístico está
basado en medidas de entropía y contrasta la hipótesis nula de que la
frecuencia espacial de lanzamiento a canasta de equipo A es igual a la
frecuencia espacial de lanzamiento del equipo B, contra cualquier otra
alternativa. El estadístico es 
que
sigue asintóticamente una distribución c2 y cuya construcción puede encontrarse
en el Apéndice.
Para ayudar al lector a entender el procedimiento
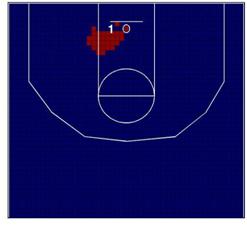
estadístico, ilustraremos el contraste de Kulldorff con un fácil ejemplo.
Consideraremos una pequeña zona de juego sobre la que hemos impuesto una
retícula regular 4´4. Supongamos que tenemos un equipo
compuesto por solo dos jugadores, jugador A y jugador B con la distribución de
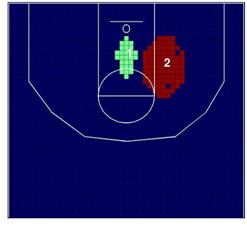
lanzamientos a canasta que se muestra en la Figura 1.
Figura1. Ejemplo básico del
test de Kulldorff
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
Jugador A |
Jugador B |
Equipo % |
En estas condiciones tenemos N=70 con nA=38
y nB=32. Entonces podemos estimar la
probabilidad de lanzamiento de un jugador simplemente dividiendo el número
total de lanzamientos del jugador en la localización s por N, por ejemplo en la
localización 1 existe una probabilidad de 0,16=(10+1)/70
(véase la tercera columna de la Figura 1). También bajo H0 la
probabilidad de lanzamiento del jugador A en cualquier localización es pA=38/70=0,54 y la del jugador B es pB=32/70=0,46
Consideremos ahora la ventana W formada por cuatro celdas
que aprecen sombreadas en la Figura 1. Entonces bajo H0 el valor
esperado de lanzamientos del jugador A es EW=34·pA= 18,45
mientras que la frecuencia real de lanzamientos es 30. Por lo tanto la ventana
W es un cluster de alta frecuencia para el jugador A. Por otro lado, bajo H0
el valor esperado de lanzamientos a canasta por el jugador B es EW=34·pB=
15,54 mientras que la frecuencia real de lanzamiento es 4 y por lo tanto la
ventana W es un cluster de baja frecuencia para el jugador B. El estadístico de
contraste de Kulldorff escanea todas las posibles ventanas en la cancha de
baloncesto buscando la máxima diferencia entre el valor esperado de frecuencia
de lanzamiento a canasta y el real y después se obtiene el p-valor mediante un
contraste de hipótesis de Monte Carlo.
Para este ejemplo también podemos calcular los valores de
las entropías y el estadístico V obteniendo h(A)=1,38, h(B)=1,31,
h(AUB)=2,31, h(A,B)=0,69 y V=41,85. Obsérvese, tal y como cabía esperar, que
V=41,85 rechaza la hipótesis nula de igualdad en la distribución espacial de
lanzamientos a canasta.
3.
RESULTADOS
Para conocer el patrón espacial de las frecuencias de
lanzamientos a canasta hemos considerado todos los partidos en las temporadas regulares
06-07, 07-08 y 08-09. Un total de 3509 partidos con 563740 lanzamientos a
canasta.
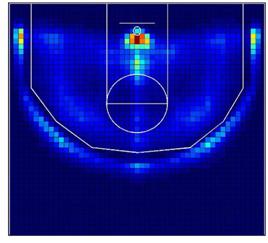
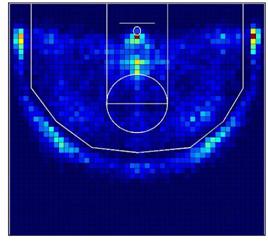
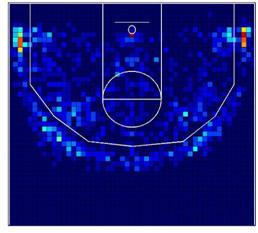
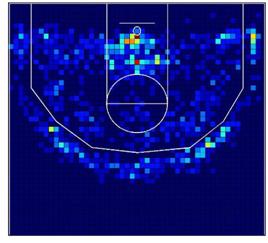
Figura 2a muestra los patrones espaciales de lanzamientos
a canasta en la NBA. Figura 2b muestra los patrones espaciales de lanzamiento
de los Lakers en las mismas tres temporadas. Las localizaciones con 0
lanzamientos se muestran en azul oscuro, que cambia a rojo conforme aumenta la
frecuencia de lanzamiento a canasta.
Figura
2.
Frecuencia de tiro de la NBA y los Lakers en las 3 temporadas consideradas.
|
|
|
|
Figura 2a: NBA |
Figura 2b: Lakers |
Existe una localización con coordenadas (26,7) con la
mayor frecuencia de lanzamiento a canasta, con una gran diferencia con las
localizaciones restantes. Esta celda contiene el 26% de los lanzamientos a
canasta de todos los equipos de la NBA y casi el 30% para los Lakers. Además,
ambos mapas muestran que las zonas de tres puntos que se encuentran al final de
la cancha en sendos lados tienen alta frecuencia de lanzamientos. Esto es un
descubrimiento lógico ya que estas zonas de tres puntos son más cercanas al aro
que las zonas de tres puntos que se encuentran enfrente del aro, debido a la no
simetría de la línea de tres puntos. En primer lugar debemos decir que ambos
mapas muestran un patrón espacial de lanzamiento a canasta similar. Sin
embargo, tras aplicar el contraste V, detectamos diferencias significativas
entre los mapas (V=2627,5; gl:1589; p-valor<0,001).
Podemos decir, de manera general, que los Lakers han orientado menos el juego
dentro de la zona que el conjunto de los equipos de la NBA.
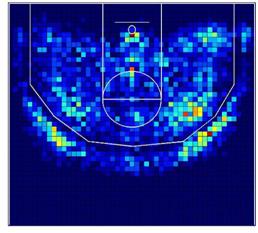
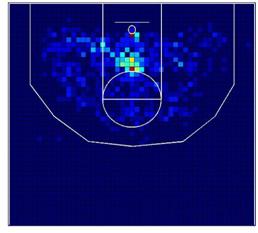
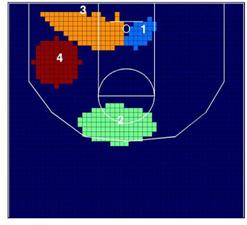
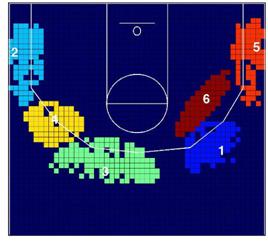
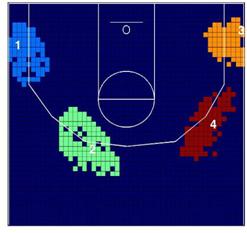
También estamos interesados en el patrón espacial de
lanzamiento a canasta de cuatro de los jugadores más importantes en los Lakers,
Kobe Bryant (KB), Pau Gasol (PG), Derek Fisher (DF) y Lamar Odom (LO). Como se
esperaba, el patrón espacial de lanzamiento entre los 4 jugadores es
divergente. De nuevo estas diferencias son lógicas, debido a las
características diferentes de los jugadores, su papel en el equipo, y su estilo
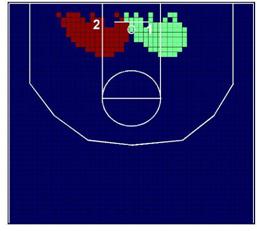
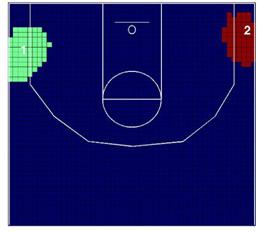
de juego. La Figura 3 muestra el patrón espacial de lanzamiento de estos cuatro
jugadores, y la Tabla 2 muestra el resultado del contraste V.
Figura
3:
Frecuencia de lanzamiento de los cuatro jugadores más importantes de los Lakers.
|
|
|
|
Figura 2a: KB |
Figura 2b: PG |
|
|
|
|
Figura 2c: DF |
Figura 2d: LO |
Tabla 2: Valores del test
V para detectar diferencias globales en el patrón espacial de lanzamientos a
canasta.
|
|
|
Lakers |
KB |
PG |
DF |
LO |
|
|
V |
2627,05 |
2523,93 |
2010,77 |
1943,78 |
1802,93 |
|
NBA |
p-valor |
<0,001 |
<0,001 |
<0,001 |
<0,001 |
<0,0011 |
|
|
gl |
1589 |
1589 |
1589 |
1589 |
1589 |
|
|
V |
|
2662,96 |
2015,17 |
1876,64 |
1696,24 |
|
Lakers |
p-valor |
|
<0,001 |
<0,001 |
<0,001 |
<0,001 |
|
|
gl |
|
1344 |
1344 |
1344 |
1344 |
|
|
V |
|
|
2019,81 |
1859,39 |
2088,97 |
|
KB |
p-valor |
|
|
<0,001 |
<0,0010 |
0,00 |
|
|
gl |
|
|
|
1199 |
1185 |
|
|
V |
|
|
|
2158,18 |
1424,41 |
|
PG |
p-valor |
|
|
|
<0,001 |
<0,001 |
|
|
gl |
|
|
|
852 |
785 |
|
|
V |
|
|
|
|
1798,22 |
|
DF |
p-valor |
|
|
|
|
<0,001 |
|
|
gl |
|
|
|
|
901 |
Nota: Los
grados de libertad (gl) de la Chi-cuadrado han sido ajustados borrando celdas
que contienen ceros.
Kobe Bryant es un jugador completo desde el punto de
vista ofensivo. Él lanza a canasta desde todas las zonas, aunque ligeramente
prefiere estar orientado alrededor de 60 grados a la derecha del aro. Por otro
lado, Pau Gasol juega como ala-pívot y como pívot, y lanza a canasta cerca del
aro, dentro de la zona, y preferiblemente orientado hacia la izquierda. Derek
Fisher está especializado en lanzamientos de tres puntos, especialmente desde
las esquinas a la derecha e izquierda del aro, más allá de la línea de tres
puntos. Y Lamar Odom, que es un ala-pívot como Gasol, es un jugador más
versátil, su juego fuera de la zona es muy importante, e incluye lanzamientos a
canasta desde la zona de tres puntos.
Como explicamos previamente, los analistas coinciden en
que la incorporación de Gasol y Fisher en la temporada 2007/08 fueron factores
clave en la transformación de los Lakers. Por tanto, vamos a analizar las
temporadas previa y siguiente a este hecho con el fin de ver si este cambio se
ha reflejado en la distribución de los lanzamientos a canasta. La Figura 4
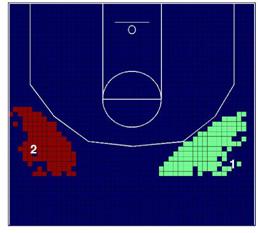
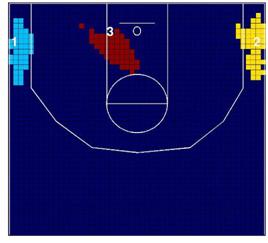
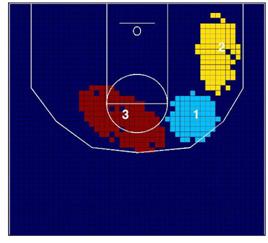
muestra los clusters de alta y baja incidencia de los Lakers en relación con la
NBA en las temporadas 2006/07 y 2008/09. Recuérdese que los clusters de alta
incidencia pueden ser interpretados como las localizaciones preferidas para
lanzar a canasta, donde los lanzamientos de los Lakers están estadísticamente
por encima de los lanzamientos esperados por toda la NBA, y lo contrario para
los clusters de baja incidencia.
Figura
4.
Clusters de baja y alta incidencia para los Lakers en relación a la NBA.
|
|
Baja
incidencia |
Alta
incidencia |
|
2006/2007 |
|
|
|
|
Figura 4a |
Figura3b |
|
2008/2009 |
|
|
|
|
Figura 4c |
Figura 4d |
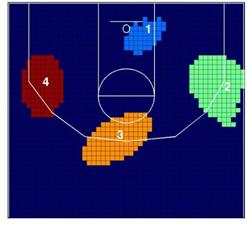
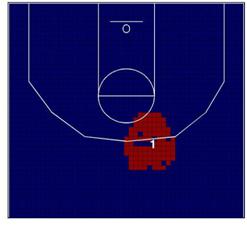
Como muestra la Figura 4a, en la temporada 2006/07, los Lakers
tenían dos clusters de baja incidencia cerca del aro (clusters 1 y 3). El
segundo cluster de baja incidencia está localizado entre la línea de tiros
libres y la línea de tres puntos, y el cuarto cluster se encuentra en una gran
zona de dos puntos en la parte media izquierda de la cancha. Parece que el
juego dentro de la zona no es el área preferida de los Lakers para lanzar a
canasta. En cualquier caso, en la temporada 2008/09 hubo un importante cambio
en el patrón espacial de lanzamiento (Figura 4c), porque los clusters 2 y 4 de
la Figura 4a se mueven hacia la línea de 3 puntos (clusters
3 y 4 de la Figura 4c), y lo que es más importante, el cluster 2 se mueve hacia
una localización distinta, en la parte media derecha de la cancha opuesto al cluster 4.
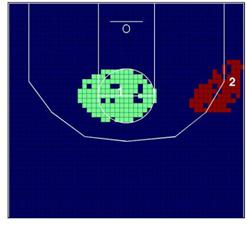
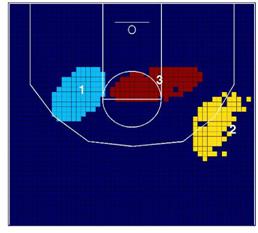
Por lo que respecta a los clusters de alta incidencia, en
la temporada 2006/07, los Lakers tuvieron dos clusters en el ángulo medio de la
línea de tres puntos (clusters 1 y 2). En cualquier caso,
en la temporada 2008/09 hubo otro cambio importante, porque el cluster 1 se
mueve hacia dentro de la zona.
Considerando que Pau Gasol normalmente juega dentro de la
zona en la parte izquierda del aro, los cambios en los cluster de alta y baja
incidencia parecen reflejar la importancia de Gasol en el patrón espacial de
lanzamiento de los Lakers. Por tanto, la incorporación de Gasol ha hecho de los
Lakers un equipo más poderoso dentro de la zona con respecto al conjunto de
equipos de la NBA. La Tabla 3 muestra algunas propiedades estadísticas de los
clusters.
Tabla
3.
Estadísticos de los clusters de baja y alta incidencia para los Lakers y la NBA.
|
Temporada |
Cluster |
Nº |
Tamaño |
OW |
EW |
Ku |
p-valor |
|
2006/2007 |
Alta |
1 |
119 |
371 |
230,56 |
35,56 |
0,001 |
|
2 |
107 |
331 |
202,34 |
34,93 |
0,001 |
||
|
Baja |
1 |
29 |
100 |
247,83 |
57,71 |
0,001 |
|
|
2 |
109 |
153 |
289,70 |
38,28 |
0,001 |
||
|
3 |
98 |
185 |
308,16 |
28,33 |
0,001 |
||
|
4 |
81 |
191 |
272,95 |
14,33 |
0,004 |
||
|
2008/2009 |
Alta |
1 |
46 |
187 |
325,72 |
35,74 |
0,001 |
|
2 |
132 |
198 |
310,06 |
23,76 |
0,001 |
||
|
3 |
111 |
215 |
321,44 |
19,68 |
0,001 |
||
|
4 |
99 |
233 |
327,06 |
15,43 |
0,001 |
||
|
Baja |
1 |
78 |
493 |
311,95 |
46,26 |
0,001 |
|
|
2 |
60 |
151 |
92,31 |
15,89 |
0,002 |
Tamaño:
Número de celdas en el cluster; OW = Número de lanzamientos
intentados observados en el cluster. EW = Lanzamientos esperados en
el cluster W. Ku = Valor del estadístico de Kulldorff.
3.1
EL JUEGO DE LOS EQUIPOS OPONENTES DE LOS LAKERS EN LAS TEMPORADAS 2006/2007 Y
2008/2009
Como el baloncesto es 50% ataque y 50% defensa, también
analizaremos el patrón espacial de lanzamiento de los oponentes de los Lakers,
para así obtener un dibujo más completo de la transformación este equipo.
Siguiendo la misma metodología, mostramos los resultados en la Figura 5.
Recuérdese que estamos comparando el patrón espacial de los oponentes de los Lakers en la temporada 2006/07 con el patrón de lanzamiento
de los oponentes de los Lakers en la temporada 2008/09, es decir después de la
incorporación de Gasol y Fisher. Si nos centramos solo en los cambios en los
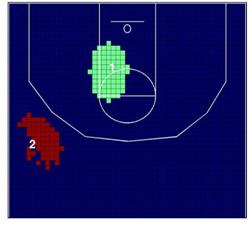
clusters, el cluster 2 de baja incidencia en la temporada 2006/07 se mueve a la
zona donde Gasol se situa normalmente en defensa en la temporada 2008/09.
Además, el cluster 1 se convierte en un cluster más
grande. Por otro lado, el cluster 3 de alta incidencia (situado dentro de la
zona) desaparece. De nuevo, globalmente estos resultados parecen indicar la
importancia de la contribución de Gasol a su equipo, porque el patrón espacial
de lanzamiento de los oponentes ha cambiado significativamente en las
principales áreas de influencia del juego de Gasol. La Tabla 4 muestra algunas
propiedades estadísticas de los clusters.
Figura
5.
Clusters de baja y alta incidencia para los oponentes de los Lakers
|
|
Baja incidencia |
Alta incidencia |
|
2006/2007 |
|
|
|
|
Figura 5a |
Figura 5b |
|
2008/2009 |
|
|
|
|
Figura 5c |
Figura 5d |
Tabla
4.
Estadísticos de los clusters de baja y alta incidencia para los oponentes de
los Lakers
|
Temporada |
Cluster |
Nº |
Tamaño |
OW |
EW |
Ku |
p-valor |
|
2006/2007 |
Alta |
1 |
111 |
217 |
130,25 |
23,51 |
0,001 |
|
2 |
39 |
111 |
53,56 |
22,48 |
0,001 |
||
|
3 |
72 |
269 |
180,25 |
19,52 |
0,001 |
||
|
4 |
27 |
100 |
60,49 |
10,73 |
0,054 |
||
|
Baja |
1 |
34 |
87 |
209,76 |
47,07 |
0,001 |
|
|
2 |
57 |
106 |
167,35 |
13,13 |
0,017 |
||
|
3 |
6 |
0 |
11,82 |
11,16 |
0,078 |
||
|
2008/2009 |
Alta |
1 |
76 |
418 |
312,56 |
16,64 |
0,002 |
|
2 |
61 |
306 |
223,94 |
13,74 |
0,003 |
||
|
Baja |
1 |
76 |
179 |
307,55 |
32,34 |
0,001 |
|
|
2 |
87 |
183 |
294,41 |
24,89 |
0,001 |
Tamaño:
Número de celdas en el cluster; OW = Número de lanzamientos
intentados observados en el cluster. EW = Lanzamientos esperados en
el cluster W. Ku = Valor del estadístico de Kulldorff.
3.2
EL JUEGO DE LOS JUGADORES MÁS IMPORTANTES DE LOS LAKERS ANTES Y DESPUÉS DE LA
INCORPORACIÓN DE GASOL
Más allá de la influencia de Gasol en el equipo de los
Lakers, también es interesante estudiar si hay algún cambio en el juego
específico de sus compañeros de equipo. Tal y como se comentó anteriormente,
Bryant y Odom fueron los más notables jugadores en el periodo pre-Gasol. Por lo
tanto analizaremos los patrones espaciales de lanzamiento a canasta de estos
dos jugadores para la temporada 2006/07 y los partidos de la temporada 2007/08
jugados antes de la incorporación de Gasol. Los resultados del contraste de
Kulldorff y la visualización gráfica de los clusters se muestran en la Tabla 5
y Figura 6, respectivamente.
Tabla
5.
Estadísticos de los clusters de baja y alta incidencia para KB y LO en el
periodo pre-Gasol
|
Jugador |
Cluster |
Nº |
Tamaño |
OW |
EW |
Ku |
p-valor |
|
KB |
Alta |
1 |
74 |
244 |
126,22 |
45,99 |
0,001 |
|
2 |
91 |
214 |
123,56 |
27,17 |
0,001 |
||
|
3 |
137 |
207 |
125,42 |
22,19 |
0,001 |
||
|
Baja |
1 |
42 |
19 |
86,03 |
37,00 |
0,001 |
|
|
2 |
46 |
34 |
92,14 |
23,51 |
0,001 |
||
|
3 |
49 |
48 |
105,42 |
17,61 |
0,001 |
||
|
LO |
Baja |
1 |
11 |
0 |
15,15 |
12,21 |
0,028 |
Tamaño:
Número de celdas en el cluster; OW = Número de lanzamientos
intentados observados en el cluster, EW = Lanzamientos esperados en
el cluster W, Ku = Valor del estadístico de Kulldorff,
Figura 6. Clusters de baja y alta incidencia para KB
y LO en el periodo pre-Gasol
|
|
Baja incidencia |
Alta incidencia |
|
|
KB |
|
|
|
|
|
Figura 6a |
Figura 6b |
|
|
LO |
|
|
|
|
|
Figura 6c |
Figura 6d |
|
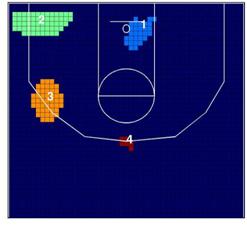
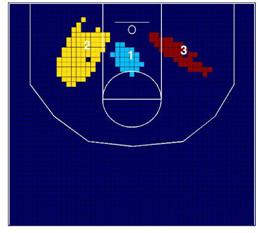
La localización de los cluster en la Figura 6 sugiere que
en el periodo pre-Gasol, Bryant prefiere lanzar a canasta desde el centro y el
lado derecho de la cancha, mientras que lanza a canasta relativamente menos
desde la zona de tres puntos localizada cerca de las esquinas de la cancha. Por
otro lado, Odom prefiere lanzar a canasta por la zona de tres puntos enfrente
del aro, en vez de lanzar desde una zona más cercana.
Sin embargo, los análisis más interesantes vienen de la
comparación del periodo pre-Gasol con el “periodo Gasol” (desde febrero de 2008
hasta el final de la temporada 2009). Los resultados del contraste de Kulldorff
y la visualización gráfica de los clusters se muestran en la Tabla 6 y Figura
7, respectivamente.
Tabla 6. Estadísticos de los
clusters de baja y alta incidencia para KB, PG; DF y LO en el “periodo Gasol”
|
Jugador |
Cluster |
Nº |
Tamaño |
OW |
EW |
Ku |
p-valor |
|
KB |
Alta |
1 |
95 |
187 |
99.31 |
32.04 |
0.001 |
|
2 |
90 |
172 |
100.50 |
21.83 |
0.001 |
||
|
3 |
88 |
133 |
72.87 |
16.66 |
0.001 |
||
|
Baja |
1 |
60 |
19 |
86.69 |
39.21 |
0.001 |
|
|
2 |
53 |
29 |
78.83 |
20.24 |
0.001 |
||
|
3 |
31 |
45 |
99.54 |
19.59 |
0.001 |
||
|
PG |
Alta |
1 |
28 |
166 |
62.07 |
62.59 |
0.001 |
|
2 |
85 |
124 |
59.17 |
27.01 |
0.001 |
||
|
3 |
40 |
59 |
27.37 |
11.27 |
0.027 |
||
|
Baja |
1 |
72 |
0 |
64.52 |
66.19 |
0.001 |
|
|
2 |
79 |
0 |
64.52 |
64.85 |
0.001 |
||
|
3 |
120 |
0 |
64.52 |
64.85 |
0.001 |
||
|
4 |
73 |
0 |
61.00 |
61.23 |
0.001 |
||
|
5 |
70 |
1 |
61.77 |
54.80 |
0.001 |
||
|
6 |
63 |
15 |
54.89 |
18.24 |
0.001 |
||
|
DF |
Alta |
1 |
74 |
105 |
42.44 |
34.28 |
0.001 |
|
2 |
104 |
99 |
40.60 |
30.13 |
0.001 |
||
|
3 |
60 |
89 |
42.14 |
21.04 |
0.001 |
||
|
4 |
83 |
84 |
42.85 |
15.49 |
0.002 |
||
|
Baja |
1 |
27 |
8 |
41.83 |
20.06 |
0.001 |
|
|
2 |
92 |
13 |
42.75 |
14.51 |
0.002 |
||
|
LO |
Alta |
1 |
23 |
37 |
13.02 |
14.71 |
0.002 |
|
Baja |
1 |
31 |
7 |
40.78 |
21.68 |
0.001 |
|
|
2 |
87 |
9 |
40.07 |
17.17 |
0.001 |
||
|
3 |
86 |
8 |
34.07 |
11.91 |
0.028 |
||
|
4 |
83 |
15 |
42.51 |
11.63 |
0.037 |
Tamaño:
Número de celdas en el cluster; OW = Número de lanzamientos
intentados observados en el cluster, EW = Lanzamientos esperados en
el cluster W, Ku = Valor del estadístico de Kulldorff.
Figura
7.
Clusters de baja y alta incidencia para KB y LO en el “periodo Gasol”
|
|
Baja incidencia |
Alta incidencia |
|
KB |
|
|
|
|
Figura 7a |
Figura 7b |
|
LO |
|
|
|
|
Figura 7c |
Figura 7d |
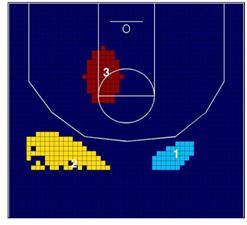
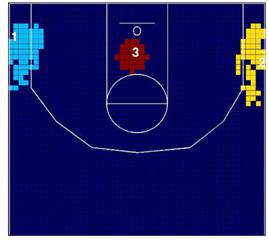
Como se observa en la Figura 7, se han encontrado cambios
significativos. Con respecto a Bryant, la zona de alta incidencia se mueve a la
izquierda de la cancha, estando más orientada al centro de la pista que
anteriormente, donde existe una diferencia muy pequeña desde los ángulos
derecho e izquierdo (aunque levemente prefiere la derecha).
En relación a Odom, ha trasladado el cluster de alta
incidencia dentro de la zona, así que la incorporación de Gasol ha hecho que
Odom lance a canasta más cerca del aro. Una explicación posible a este aumento
de lanzamientos se puede atribuir al aumento de rebotes ofensivos conseguidos
por Odom desde la incorporación de Gasol. Nótese que la media de rebotes
ofensivos por partido de Odom fue de 1,8 en la temporada 2006/07 y 2,14 en la
porción de la temporada 2007/08 jugada sin Gasol. Desde la llegada de Gasol,
Odom consiguió 3,02 rebotes ofensivos en la temporada 2007/08 y 2,30 en la
temporada 2008/09. Parece evidente el aumento de la contribución de Odom a esta
parte del juego de los Lakers desde el traspaso de Gasol.
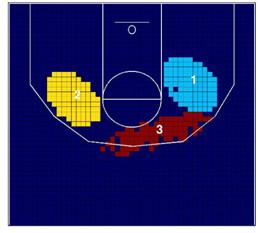
Por lo que se refiere a Gasol, existen tres clusters de
alta incidencia localizados dentro de la zona y en un área a 4-5 metros. Es
claro que Gasol ligeramente prefiere lanzar a canasta desde el lado izquierdo
del aro. Finalmente Fisher muestra un patrón de lanzamiento consistente con su
especialidad, el lanzamiento de tres puntos. La Figura 8 muestra los clusters de Gasol y Fisher.
Figura
8.
Clusters de baja y alta incidencia para PG y DF en el “periodo Gasol”
|
|
Baja incidencia |
Alta incidencia |
|
PG |
|
|
|
|
Figura 8a |
Figura 8b |
|
DF |
|
|
|
|
Figura 8c |
Figura 8d |
4.
DISCUSIÓN, LIMITACIONES E INVESTIGACIONES FUTURAS
En este artículo hemos
mostrado una aplicación de la estadística espacial para comprender mejor
ciertos aspectos del juego en baloncesto. Esta metodología ha sido poco
utilizada en la investigación en deporte, y más específicamente en baloncesto.
Hemos expuesto una contribución interesante de esta perspectiva metodológica en
el caso del análisis de la actuación de los Lakers, y
de la transformación de este equipo de una franquicia de nivel medio de la NBA
a un equipo campeón.
Hemos explicado,
como una técnica de identificación de cluster espaciales, como es el contraste
de Kulldorff, puede ser aplicada al análisis de datos
de baloncesto. Este contraste detecta clusters de baja y alta incidencia del
número de lanzamientos a canasta, y por lo tanto caracteriza el juego de los
equipos y jugadores individualmente mucho mejor. Además, también hemos usado el
contraste basado en entropía, el contraste V, que sirve para comparar mapas de
lanzamientos a canasta desde un punto de vista estadístico.
Combinando ambos
métodos, hemos encontrado como la incorporación de dos jugadores: Dereck
Fisher, y especialmente Pau Gasol, han ido asociados con el cambio en los
patrones espaciales de lanzamiento a canasta de los Lakers. Además, no sólo se
ha visto afectado el juego atacante sino también el defensivo, porque también
cambió el patrón espacial de los lanzamientos a canasta de los oponentes. La
figura de Pau Gasol emerge como la razón principal de estos cambios, debido a
la aparición de algunos clusters en la cancha donde Gasol suele jugar. Los Lakers han intensificado el juego dentro de la zona después
de la llegada de Gasol, y probablemente ha causado que los oponentes lancen a
canasta menos de lo esperado en la zona donde Gasol suele jugar en defensa.
Además, algunos jugadores, en particular la superestrella Kobe Bryant ha
cambiado su juego, ya que los clusters espaciales de
alta incidencia en número de lanzamientos de este jugador se han movido unos
grados a la izquierda de la cancha.
Toda la información
derivada de este análisis espacial debería complementar otras estadísticas
básicas y avanzadas que se pueden encontrar de manera gratuita en páginas web
especializadas. Estas estadísticas, basadas en los box scores (resumen de estadísticas básicas del jugador) y en los datos play-by-play (datos jugada a jugada), junto con los datos de
localización espacial, deben servir para obtener un dibujo completo de la
actuación de equipos y jugadores. De hecho, como explica Ballard (2009),
algunos equipos como los Houston Rockets, han usado
esta información para indicar a sus jugadores el estilo de juego de los
oponentes (ej. informaban al jugador especializado en defensa, Shane Battier,
sobre el juego de las estrellas del equipo oponente). Usando la estadística
espacial como hemos hecho en esta investigación, se puede proporcionar
información muy útil para este propósito, debido a la distinción entre los
clusters espaciales de lanzamiento a canasta de alta y baja incidencia.
Estos análisis
pueden ser extendidos a otros equipos utilizando el mismo procedimiento. Un
claro ejemplo podría ser el caso de los Boston Celtics, que hicieron una
transformación similar en la temporada 2007/08, ganando la NBA contra los
Lakers. Obsérvese que Boston tuvo un muy pobre porcentaje de victorias (29%),
el segundo peor de su historia, en la temporada 2006/07. Entonces, esta
franquicia fichó dos jugadores All-Star: Ray Allen y Kevin Garnett, y su
actuación en la temporada siguiente fue completamente diferente; Boston obtuvo
un porcentaje de victorias de 80% (el tercero mejor de su historia). También se
pueden realizar comparaciones de un equipo contra otro equipo o un conjunto de
equipos similares. Por ejemplo, podría ser interesante realizar un análisis benchmark, comparando los Lakers
con un conjunto de equipos en el mismo “grupo estratégico” (es decir, equipos
de similar potencial) para eliminar el ruido causado por equipos con una
actuación de perfil bajo, como los equipos que no han llegado a los play-offs.
Hemos realizado dicho análisis (está disponible por los autores bajo petición)
y hemos encontrado resultados similares al caso en que lo comparamos con toda
la NBA. De nuevo un cluster de alta incidencia apareció en la temporada 2008/09
en la zona donde Gasol suele jugar.
La perspectiva que
hemos adoptado en esta investigación es una de las diferentes maneras en las
que se puede incorporar el análisis espacial con el objeto de entender mejor un
deporte. Por ejemplo, otra investigación puede analizar los patrones de
lanzamientos a canasta realizados, para detectar clusters de alta y baja
incidencia de alto porcentaje y bajo porcentaje de localizaciones. Además, el
tamaño de las celdas se puede aumentar para obtener más datos por localización,
pero aceptando el riesgo de ser menos exacto en la asignación de lanzamientos a
canasta a las localizaciones espaciales. En cualquier caso, se pueden realizar
simulaciones para explorar la consistencia de los clusters obtenidos bajo
diferentes tamaños de celdas.
Por tanto, esta investigación es totalmente novedosa en ciencias del deporte, y por supuesto en baloncesto, donde como hemos comentado sólo los estudios de Hickson y Waller (2003) y Reich, Hodges, Carlin y Reich (2006) han intentado estudiar este fenómeno, aunque de manera totalmente diferentes, y enfocándose en un solo jugador. Los esfuerzos de otros investigadores, como Piette, Sathyanarayan y Kai, (2010) en el estudio de las habilidades del lanzamiento de los jugadores son asimismo notables. Recordemos que no todos los tiros tienen la misma dificultad, por lo que la probabilidad de encestar podría ser diferente para una misma localización. Por eso nuestro estudio se enfoca en los lanzamientos intentados (convertidos y fallados), porque hacerlo sólo en los convertidos podría ocasionar problemas derivados de las diferentes probabilidades de acierto en función de su dificultad.
5.
CONCLUSIONES
A través de la aplicación de técnicas de estadística
espacial, como el test de Kulldorff, y un test no
paramétrico basado en entropía, el test V, hemos mostrado como se puede
analizar el patrón de lanzamientos de los jugadores y equipos de baloncesto. De
este modo, se dispone de una herramienta estadística que permite estudiar y
comparar diferentes jugadores y equipos desde el punto de vista de su
localización espacial de lanzamientos a canasta, lo que es muy útil para
detectar los lugares de la cancha donde se prefiere lanzar.
De manera empírica, hemos ilustrado cómo el fichaje de Pau
Gasol por los Lakers en la temporada 2007/2008 cambió la manera de jugar de
este equipo (incluyendo sus jugadores clave), y también la de los rivales. Así,
la transformación de los Lakers en un equipo campeón, no sólo se ha visto
reflejada en las estadísticas evidentes y básicas de productividad de los
jugadores, sino también en la forma de juego, al menos en cuanto a localización
espacial de lanzamiento.
Finalmente, y de manera general, el uso de las herramientas
descritas en este artículo puede ayudar a los equipos de baloncesto a analizar
el juego de sus rivales desde el punto de vista espacial, yendo más allá de los
datos simples de localización de lanzamiento, que son meramente descriptivos y
no proporcionan ningún criterio estadístico de comparación entre el patrón de
juego de jugadores o equipos.
REFERENCIAS BIBLIOGRÁFICAS
Alferink, L. A.,
Critchfield, T. S., Hitt, J. L., y Higgins, W. J. (2009). Generality
of the matching law as a descriptor of shot selection in basketball. Journal
of Applied Behavior Analysis, 42 (3), 595-608.
Arkes, J.
(2010). Revisiting the Hot Hand Theory with free throw data
in a multivariate framework. Journal of
Quantitative Analysis in Sports, 6 (1), Article 2.
Arkes, J. y
Martinez, J. A. (2011). Finally,
Evidence for a Momentum Effect in the NBA. Journal of
Quantitative Analysis in Sports, 7
(3) Article 13.
Ballard, C.
(2009). The art of a beautiful game. Simon y
Shuster: New York
Balsdon,
E., Fong, L., y Thayer, M. (2007). Corruption in College basketball? Evidence
of tanking in postseason conference tournaments. Journal of Sports
economics, 8 (1), 19-38
Bar-Elia
M, Avugos S. y Raab M. (2006). Twenty
years of “hot hand” research review and critique. Psychology of Sport and Exercise, 7, 525-553.
Berri,
D. J. (1999). Who is 'most valuable'? Measuring
the player's production of wins in the National Basketball Association. Managerial
and Decision Economics, 20,
411-427.
Berri,
D. J. (2008). A simple measure of worker
productivity in the National Basketball Association. in
The Business of Sport, eds. Brad Humphreys and Dennis Howard, editors, 3
volumes, Westport, Conn.
Berri,
D. J., y Bradbury, J. C. (2010). Working in the land of
metricians. Journal of Sports Economics, 11 (1), 29-47.
Berri, D. J.,
y Eschker, E. (2005). Performance when it counts? The myth of
the prime time performer in professional basketball. Journal of
Economic Issues, 1, 798-807
Berri, D. J.,
y Schmidt, M. B. (2002). Instrumental versus bounded rationality: a comparison
of Major League Baseball and the National Basketball Association. Journal of
Socio-Economics, 31, 191-214.
Berri, D. J.,
y Schmidt, M. B. (2006),. On the
road with the National Basketball Association's superstar externality. Journal
of Sports Economics, 7 (4), 347-358.
Berri, D. J.,
Brook, S. L, Frick, B, Fenn, A. J., y Vicente-Mayoral, R. (2005) The short supply of tall people: competitive imbalance and
the National Basketball Association. Journal of Economic Issues, 39
(4), 1029-1041
Berri, D. J.,
Brook, S. L., y Schmidt, M. B. (2007). Does One Simply Need to Score to Score? International
Journal of Sport Finance, 2 (4), 190-205
Berry,
S. M, Reese, C. S., y Larkey, P. L. (1999) Bridging different eras in sports. Journal
of the American Statistical Association, 94, 661-686.
Bodvarsson, O.
B., y Brastow, R. T. (1998). Do employers pay for consistent performance?: Evidence from the NBA. Economic Inquiry, 36
(1), 145-160.
Bourbousson, J., Sève, C., y McGarry, T. (2010). Space-time coordination
dynamics in basketball: Part 2. The interaction between the
two teams. Journal of Sports Sciences, 28 (3), 349-58
Breshnahan, M.
(2010, 31 January). Pau Gasol's trade to Lakers changed the NBA. Descargado desde http://articles.latimes.com/2010/jan/31/sports/la-sp-lakers-gasol31-2010jan31
Chen, H.-T.,
Tien, M.-C., Chen, Y.-W., Tsai, W.-J., y Lee, S.-L. (2009). Physics-based
ball tracking and 3D trajectory reconstruction with applications to shooting
location estimation in basketball video. Journal of Visual Communication and
Image Representation 20 (3), 204-216.
Dwass,
M. (1957). Modified
randomization tests for nonparametric hypotheses. Annals of Mathematical
Statistics 28, 181–187.
Doolittle, B.
Y Pelton, K. (2009). Pro Basketball
Prospectus 2009-10. Prospectus Entertainment Ventures LLC.
Esteller-Moré,
A., y Eres-García, M. (2002). A note on
consistent players’ valuation. Journal of Sports Economics,
3 (4), 354-360.
Fernández, J.,
Camerino, O., Anguera, M. T., y Jonsson, G. K. (2009). Identifying and
analyzing the construction and effectiveness of offensive plays in basketball
by using systematic observation. Behavior Research Methods, 41,
719-730.
Fort,
R., y Maxcy, J. (2003). Competitive balance in sports leagues: An
introduction. Journal of Sports Economics, 4 (2), 154-160.
Fort,
R., Hoon-Lee, Y., y Berri, D. J. (2008). Race, technical efficiency and retention. The
case of NBA coaches. International Journal of Sport Finance, 3,
84-97.
Gilovich, T., Vallone, R. y Tversky,
A. (1985). The hot hand in basketball: On the misperception of
random sequences. Cognitive Psychology 17,
295-314.
Hickson, D.
A., y Waller, L. A. (2003). Spatial analyses of basketball shot charts: An
application to Michael Jordan’s 2001–2002 NBA season, Technical
Report, Department of Biostatistics, Emory University.
Hitt, J. L.,
Alferink, L. A., Critchfield, T. S., y Wagman, J. B. (2007). Choice behavior
expressed in elite sport competition: Predicting shot selection and game
outcomes in college basketball. In L. A. Chiang (Ed.), Motivation
of exercise and physical activity (pp.79–91). Hauppauge, NY: Nova
Science.
Hollinger, J.
(2005). Pro Basketball Forecast. Washington,
D.C.: Potomac, Inc.
Hoon-Lee, Y., y Berri, D. J. (2008). A
re-examination of production functions and efficiency estimates for the
National Basketball Association. Scottish Journal of Political Economy, 55
(1), 51-66.
Humphreys, B.
R. (2000). Equal pay on the hardwood: the earnings gap between male and female
NCAA. Division I Basketball coaches. Journal of
Sports Economics, 1 (3) 299-307.
Humphreys, B.
R. (2002). Alternative measures of competitive balance in sports leagues. Journal
of Sports Economics, 3 (2), 133-148
Jäger, J. M.,
y Schöllhorn, W. I. (2007). Situation-oriented recognition of
tactical patterns in volleyball. Journal of Sports Sciences, 25 (12),
1345-1353.
Kleeman, R.
(2009, 12 February). Pau Gasol Powers Runaway Lakers: How One Trade Changed the
Title Race. Descargado
desde http://bleacherreport.com/articles/123235-pau-gasol-powers-runaway-lakers-how-one-trade-changed-the-title-race
Kubatko, J.; Oliver, D., Pelton, K, y
Rosenbaum, D. T. (2007). A starting
point for analyzing basketball statistics. Journal of
Quantitative Analysis in Sports, 3 (3), Article 1.
Kulldorff
M. (1997) A spatial scan statistic. Communications
in Statistics: Theory and Methods, 26, 1481-1496.
Lehmann,E.L. (1986) Multivariate Linear Hypothesis. Testing statistical hypothesis.
2nd edn. John Wiley y Sons, Inc, New
York.
Lewis, M. M.
(2003) Moneyball: The art of winning an unfair game. W.W.
Norton y Company Inc.
Manning,
(2009, 14 December). Popovich: “Pau Gasol changed the landscape of basketball
in the NBA” Descargado desde
http://thelakersnation.com/blog/2009/12/14/popovich-pau-gasol-changed-the-landscape-of-basketball-in-the-nba/
Martínez, J. A. (2010). Una revisión
de los sistemas de valoración de jugadores de baloncesto (II). Competiciones
oficiales y ligas de fantasía. Revista Internacional de Derecho y Gestión
del Deporte, 11, 48-68.
Mavridis, G.,
Tsamourtzis, E., Karipidis, A., y Laios, A. (2009). The
inside game in World Basketball. Comparison between European and NBA teams. International
Journal of Performance Analysis of Sport, 9, 157-164.
Michaelides,
M. (2010). A new test of compensating differences: Evidence on
the importance of unobserved heterogeneity. Journal of Sport Economics, 11 (5),
475-495.
Mulrooney,
T. (2010). Mapping the landscape of collegiate
wrestling using spatial statistics. Timothy J. Mulrooney, 29 Nov 2007. Web. 18 Nov 2010. <http://myweb.wssu.edu/mulrooneyti/research.htm>.
Oliver,
D. (2004). Basketball on paper. Rules and tools for performance analysis. Washington, D.
C.: Brassey’s, INC.
Piette, J.,
Sathyanarayan, A., y Kai, Z. (2010). Scoring and shooting abilities of NBA
players. Journal of Quantitative Analysis in Sports, 6
(1), Article 1.
Price, J., y
Wolfers, J. (2010). Racial discrimination among NBA referees. Quarterly
Journal of Economics, 125 (4),
1859-1887
Reich, B. J.,
Hodges, J. S. Carlin, B. P., y Reich, A. M. (2006). A spatial analysis of
basketball shot chart data. The American Statistician, 60 (1), 3-12.
Rimler, M. S.,
Song, S., y Yi, D. T. (2010). Estimating
production efficiency in men’s NCAA college basketball: A bayesian approach. Journal
of Sports Economics, 11 (3), 287-315.
Romanowich,
P., Bourret, J., y Vollmer, T. R. (2007). Further analysis of
the matching law to describe two- and three-point shot selection by
professional basketball players. Journal of Applied Behavior Analysis,
40, 311–315.
Sánchez, J.
M., Castellanos, P., y Dopico, J. A. (2007). The winning production function:
Empirical evidence from Spanish basketball. European Sport Management
Quarterly, 7 (3), 283-300.
Sanderson, C.
(2010, 13 July). Why Derek Fisher Is So Important To the L.A. Lakers' Success. Descargado desde http://bleacherreport.com/articles/419819-why-derek-fisher-is-so-important-to-the-lakers-success
Skinner, B.
(2010). The price of anarchy in basketball. Journal of Quantitative Analysis in Sports, 6 (1), Article 3.
Tauer,
J. M., Guenther, C. L., y Rozek, C. (2009). Is there a home
choke in decisive playoff basketball games?. Journal
of Applied Sport Psychlogy, 21, 148-162.
Trininic,
S., Dizdar, D., y Luksic,
E. (2002). Differences
between winning and defeated top quality basketball teams in final tournaments
of European club championship. Collegium Antropologicum, 26 (2),
521-531.
Vergin,
R. C. (2000). Winning streaks in sports and the
misperception of momentum. Journal of Sport Behavior 23, 181-197.
Vollmer, T.
R., y Bourret, J. (2000). An application of the matching law
to evaluate the allocation of two and three-point shots by college basketball
players. Journal of Applied Behavior Analysis, 33,
137–150.
Winston, W. L.
(2009). Mathletics. New Yersey: Princeton
University Press
Zimmer,
T., y Kuethe, T. H. (2007). Testing for bias
and manipulation in the National Basketball Association playoffs. Journal
of Quantitative Analysis in Sports, 5 (3), Article 4.
Referencias totales / Total references: 58 (100%)
Referencias propias de la revista / Journal's own references: 0
Rev.int.med.cienc.act.fís.deporte- vol. 13 - número 51
- ISSN: 1577-0354
APÉNDICE
Para dar una respuesta a esta pregunta supondremos que la
cancha de balonmcesto es una retícula regular 
L. En cada localización sÎL
denotaremos por 
el número total de lanzamientos a canasta en
la localización s realizados por el jugador (resp. equipo) A. Similarmente
denotaremos por 
el número total de lanzamiento a canasta
realizados en la localización s por el jugador (resp. equipo) B. Denotamos por 
,
,
y 
el
número total de lanzamientos a canasta en la localización s y el número total
de lanzamientos realizados por los jugadores A, B y AÈ B (resp.
equipos) respectivamente. Entonces uno puede fácilmente calcular la frecuencia relativa
en la loicalización s y el número total de lanzamientos de A y B mediante 
,
,
y 
respectivamente. Así la frecuen cia relative
del total de lanzamientos en la
localización s es
.
Ahora
bajo este scenario podemos definer la entropía del total de lanzamientos.
Esta entropía se define como la entropía de Shannon de la distribución de 
como sigue:
La
entropía del total de lanzamientos, h(AÈB), es la
información contenida en la comparación de la distribución de r en todas las
localizaciones en L.
Análogamente
tenemos la entropía de lanzamientos de A, B y A versus B
y
respectivamente.
Una
vez introducidas las definiciones básicasy la notación necesaria construiremos
un contraste estadístico para comprobar si la distribución de los lanzamientos
a canasta realizados por el jugador A es igual a la distribución de los
lanzamientos a canasta del jugador B. Con este fin consideramos la siguiente
hipótesis nula:
H0: La distribución de los lanzamientos a canasta
es la misma para el equipo A que para el equipo B
es
decir,
para
todo sÎL.
Supongamos
que la retícula L tiene cardinal R. Nótese que la variable “número de
lanzamientos en la localización s” es una variable aleatoria que se distribuye
como una Binomial que se puede escindir en dos distribuciones Binomiales Ys=B(N,ps) y Zs=B(N,qs)
correspondientes a los equipos A y B respectivamente.
Por
lo tanto la function de densidad conjunta de las 2R variables es
donde
y su function de
verosimilitud es:
.
Es
inmediato ver que los estimadores máximo verosimiles de 
,
y
son
,
y 
respectivamente.
Entonces,
bajo la nula H0 tenemos que y así, 
. Por lo tanto bajo la nula H0, el estadístico
del ratio de verosimilitud es (véase Lehmann (1986))
.
Por
otro lado V= -2 ln(l)
asintóticamente siguen una distribución Chi-cuadrado con R-1 grados de libertad
véase por ejemplo Lehmann (1986)). Lueoobtenemos que el estimador 
de
V es
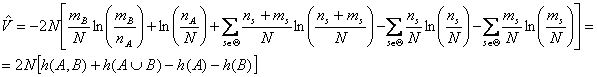
Que se
distribuye como 
.
Rev.int.med.cienc.act.fís.deporte- vol. 13 - número 51
- ISSN: 1577-0354