 Martínez, J.A. (2014). La
influencia del primer cuarto en el resultado final en baloncesto / The influence of the first quarter
on the final result in basketball. Revista
Internacional de Medicina y Ciencias de la Actividad Física y el Deporte
vol. 14 (56) pp. 755-769 Http://cdeporte.rediris.es/revista/revista56/artinfluencia513.htm
Martínez, J.A. (2014). La
influencia del primer cuarto en el resultado final en baloncesto / The influence of the first quarter
on the final result in basketball. Revista
Internacional de Medicina y Ciencias de la Actividad Física y el Deporte
vol. 14 (56) pp. 755-769 Http://cdeporte.rediris.es/revista/revista56/artinfluencia513.htm
ORIGINAL
LA INFLUENCIA DEL PRIMER CUARTO EN EL RESULTADO FINAL EN
BALONCESTO
THE INFLUENCE OF THE FIRST QUARTER ON THE
FINAL RESULT IN BASKETBALL
Martínez, J.A.
josean.martinez@upct.es, http://www.upct.es/~beside/jose,
Profesor Contratado Doctor. Departamento de Economía de
Código UNESCO / UNESCO Code: 5899
Educación Física y Deporte / Physical Education and Sport
Clasificación
Consejo de Europa /Classification Council of Europe:
17 Otras: Análisis cuantitativo del deporte / Other:
Quantitative analysis of
sport
Recibido 30 de enero
de 2012 Received
January 30, 2012
Aceptado 8 de enero
de 2013 Accepted January 8,
2013
RESUMEN
Esta
investigación analiza la influencia que tiene el resultado en el primer
cuarto de un partido de baloncesto sobre el marcador final, con el fin de
detectar precozmente situaciones problemáticas para los equipos y
dilucidar la probabilidad de victoria desde los primeros minutos de juego.
Así se han implementado varios modelos estadísticos basados en la
modelización del patrón temporal de resultados parciales:
autorregresivos, trayectorias latentes, autorregresivos de trayectorias
latentes y path logit. Los resultados
indican que es preferible comenzar ganando, ya que la dependencia del estado
temporal anterior del resultado es muy alta. Ir ganando en el primer cuarto es
fundamental para obtener la victoria en el partido, si bien ello también
depende, aunque en mucha menor medida, de si el equipo juega o no en casa y de
la diferencia de potencial entre los contendientes.
PALABRAS CLAVES: baloncesto,
detección precoz, predicción resultado, datos longitudinales
ABSTRACT
This
research analyses the influence of the outcome in the first quarter of a
basketball game on the final result. The aim is to early detect alarm states
for teams and to compute the probability of win from data obtained from the
first minutes of the game. To achieve this goal, several statistical models
based on modeling change in partial results have been tested: autoregressive,
latent growth, autoregressive latent growth and path logit. Results show it is desirable
to start winning the game, because the dependence of each partial outcome from
the early outcome is noticeable. Therefore, to win the first quarter is
essential to win, although to a lesser extent this also depends on the home
advantage and the difference of quality of the teams.
KEYWORDS:
basketball, early detection, predicting
results, longitudinal data
1. INTRODUCCIÓN
En
prácticamente la totalidad de las disciplinas científicas la
detección precoz es capital, ya que ésta permite anticiparse a
los eventos futuros, emitir diagnósticos e implementar las acciones
necesarias para mejorar las consecuencias de ese estado proyectado. En ciencias
del deporte, probablemente la detección de talentos es el área
donde más se ha puesto énfasis en la detección precoz (ej.
Falk, Lidor, Lander y Lang, 2004), aunque también existen
múltiples investigaciones que tratan de predecir el rendimiento de
equipos y deportistas, y resultados de competiciones a través de modelos
estadísticos (ej. Brown y Sokol, 2010; Caudill y Godwin, 2002).
De
especial interés resultan los estudios que tratan de conocer la
influencia de resultados iniciales sobre la clasificación final de los
equipos, como el realizado por Lago y Casáis (2010). En esa
investigación (en el ámbito del fútbol profesional), estos
autores encuentran que para los equipos con los presupuestos más bajos,
los rendimientos obtenidos en los primeros partidos de la competición
tienen un impacto muy fuerte sobre su clasificación final. Por tanto,
esos equipos deberían de tratar de comenzar lo más fuerte posible
la temporada, diseñando para ello una pretemporada acorde a esos
objetivos.
Pero,
¿qué ocurre con la predicción del resultado de un partido
en base al rendimiento en los primeros minutos de juego? De igual forma que
Lago y Casáis (2010) recomiendan “empezar ganando” en los
primeros partidos de la temporada, ¿se podrían establecer
conclusiones similares para los resultados de un partido? Éstas son las
cuestiones que trata de responder esta investigación, y para ello se han
analizado 3103 partidos de baloncesto en tres temporadas en la NBA, usando como
variable de predicción los resultados de los equipos en el primer cuarto
de cada partido. Así, el objetivo de este estudio es analizar la relación
entre el rendimiento de los equipos al comienzo de cada partido y el resultado
final, con el fin de dilucidar la probabilidad de victoria desde los primeros
minutos de juego.
Aunque
existen otras investigaciones que han tratado de explicar el resultado final de
un partido en base al resultado en la mitad del mismo (ej. Cooper, DeNeve y
Mosteller, 1992), y que han encontrado una asociación positiva entre el
rendimiento en ambos momentos, ésta es probablemente la primera
investigación que trata esta temática en un momento del juego
más inicial, como es el primer cuarto del partido, por lo que puede
arrojar mayor luz sobre la importancia de los primeros minutos de juego en el
resultado final de un partido. De este modo, conociendo el modelo que rige el
patrón de resultados parciales en un partido, los factores asociados al
cambio en el resultado, y la influencia de éstos en la probabilidad de
victoria, los equipos pueden detectar precozmente situaciones
problemáticas, y tratar de ajustar su juego ante tales eventos.
2.
MÉTODOLOGÍA
2.1.
DATOS Y VARIABLES
Los
datos fueron adquiridos de www.nbastuffer.com,
donde se dispone de información sobre el resultado en la NBA en cada
cuarto del partido. Se obtuvieron así datos de las temporadas 2006/07,
2007/08 y 2008/09, en la competición regular, por lo que un total de
3690 partidos componían la base inicial.
Las
variables de análisis fueron las siguientes: En primer lugar se
registró el marcador de cada partido en 4 momentos del tiempo
diferentes: primer cuarto (y1), segundo cuarto (y2), tercer cuarto (y3) y
cuarto cuarto (y4), con el fin de tener un dibujo de los diversos estadios del
resultado del partido en función del tiempo de juego. La variable y4 se
refiere al marcador final cuando no existe prórroga. Estas 4 variables
son continuas, a las que se añadió el registro de una variable
binaria (y5) que determinaba si el equipo de casa había ganado el
partido o no, es decir, reflejaba si y4>0 con un “1” y con un
“0” el caso contrario.
En
segundo lugar se identificaron covariables que podrían incidir en el
resultado del partido. Para ello, se tomaron como referencia los estudios de
Arkes y Martínez (2011) y Martínez (2012). Estos autores modelan
el resultado de los partidos de baloncesto utilizando diversas covariables,
siendo las más relevantes el factor cancha, la diferencia de potencial
entre los equipos y el tipo de partido (en función de la calidad de los
contendientes). Otras variables como los días de descanso, o las rachas
de juego tienen también efecto sobre el resultado, pero su incidencia es
mucho menor que esas tres variables comentadas. Por ello, y en aras de
simplificar los análisis, se obviaron en este estudio.
Como
el registro de y1-y4 se realizó siempre tomando como referencia el
equipo local, entonces el factor cancha queda implícitamente
considerado. La diferencia de potencial entre los equipos (x1) se
calculó utilizando la diferencia en el porcentaje de victorias al final
de la temporada, siguiendo a Martínez (2012). Es una variable acotada en
un intervalo [0,1]. Este autor también describe las
características de la variable que hace referencia al tipo de partido
(x2): El valor absoluto de la diferencia entre el porcentaje de victorias de
los equipos transformado en función de un parámetro exponencial.
Como en la NBA existe interacción entre la ventaja campo y la calidad de
los equipos, los equipos con menor potencial son relativamente más
fuertes en casa que aquellos con mayor potencial. Por tanto, el valor del
parámetro hace referencia a
la suma del potencial de ambos equipos (mínimo cero y máximo
dos). De este modo, para equipos con una diferencia de potencial similar, el
valor de x2 se incrementa si los dos equipos tienen un porcentaje de victorias
elevado en comparación a si lo tienen bajo. Por ejemplo, x2=0.63 cuando se enfrentan dos equipos
con porcentaje de victorias 1 y 0,5, respectivamente. Mientras que x2=0.31 si
ambos equipos tienen porcentajes de 0,6 y 0,1 respectivamente. Es decir, ante la
misma diferencia de potencial, x2 corrige por el potencial de ambos equipos
(algo así como un factor de “calidad” del partido). Es una
variable limitada en un rango [0,1].
Una
vez identificadas las variables del análisis, se procedió a realizar
una depuración de los datos. En primer lugar, se siguieron las
recomendaciones de Wilcox (2010) para recortar un 5% de ambas colas de la
distribución de datos ordenados. Para ello se escogió el
resultado final del partido como variable de referencia. El objetivo era
eliminar aquellos partidos cuya diferencia en el marcador fuera
extraordinariamente alta para el equipo de casa o para el de fuera en
función de la distribución de los datos, ya que ello
podría ser identificativo de casos atípicos. De este modo, el
rango de diferencia de puntos se limitó a (-18 ;
+24), quedando fuera del análisis los partidos en los que el equipo
visitante ganó por más de 18 puntos y el local por más de
24. Un segundo criterio de exclusión fue el relativo a la consideración
de los partidos con prórroga. Estos partidos deben eliminarse del
análisis ya que tienen características diferentes que impiden la
homogeneidad del contexto de análisis. Así, su duración es
mayor (había varios partidos incluso con 3 prórrogas), por lo que
el efecto de los marcadores parciales sobre el resultado final pierde la
homogeneidad temporal. Un total de 221 partidos se eliminaron por esta
razón, que contribuyeron al total de 587 partidos que finalmente se
excluyeron debido de los dos criterios de filtrado. Por tanto, la base de datos
final susceptible de ser analizada estaba compuesta por 3103 partidos.
2.2.
MODELOS ESTADÍSTICOS
Para
estudiar en qué medida el resultado del primer cuarto del partido puede
influir en el resultado final del mismo se realizaron diversas aproximaciones
estadísticas.
En
primer lugar, se modeló el patrón temporal de resultados y1-y4.
El objetivo era identificar el mejor modelo que representase los datos
empíricos. Para ello tres tipos de modelos fueron candidatos al
análisis: los modelos autorregresivos (AR), los modelos latentes de
trayectorias (LT) y los modelos autoregresivos latentes de trayectorias (ALT).
Los
modelos AR ejemplifican la transición de una variable de un momento
temporal a otro, donde el estado en un momento del tiempo depende
únicamente del estado anterior más un término de error
aleatorio. Por el contrario, los modelos LT permiten modelar la tendencia de
cada caso en el tiempo, a través de la especificación de un
parámetro intercept y una
pendiente, es decir, se enfocan en la trayectoria de cambio de cada individuo
en el tiempo, mientras que en los modelos AR los efectos de un periodo del
tiempo sobre otros son iguales para todos los individuos. En los modelos AR
estaríamos hablando de efectos fijos, mientras en los modelos LT de
efectos aleatorios. La integración de ambos modelos constituyen los
modelos ALT, que cubren las desventajas de los modelos anteriores, pero que a
cambio tienen inconvenientes derivados de las condiciones de identificación
para la estimación (Bollen y Curran, 2004), lo que hace que por ejemplo
se deban especificar los parámetros intercept
y pendiente correlacionados con y1, es decir, la primera medición
temporal se saca fuera de la parte LT del modelo ALT. Todos estos modelos
permiten la integración de covariables, aunque hay autores como Kline
(2011) que recomiendan primero escoger el modelo base que se ajuste a los
datos, antes de añadir covariables. Este procedimiento es criticado por
Hayduk (1996) quien defiende la estimación de los modelos en un solo
paso.
En
cualquier caso, la estrategia de análisis fue la comparación de
diferentes modelos vía chi-cuadrado, en aras de determinar cuál
era el mejor modelo que se ajustaba a los datos, y así entender el
patrón de cambio en el resultado de un partido en función del
tiempo. Una explicación más extensa y técnica de este tipo
de modelos puede encontrarse en Bollen y Curran (2004) y en Morin, Maïano,
Marsh, Janosz y Nagengast (2011).
En
segundo lugar, y una vez entendido un modelo que se ajuste a la
evolución temporal del marcador, se relacionó y1 con y5, es
decir, el marcador en el primer cuarto con el resultado final del partido,
controlando por las covariables x1 y x2. A través de la implementación
de regresiones logística se estudió el efecto marginal de y1
sobre y5, con el fin de obtener una conclusión más clara sobre
cómo actúa el marcador del primer cuarto sobre el resultado
final.
3.
RESULTADOS
Para testar los diferentes modelos
candidatos a reflejar el patrón de cambio en el resultado se
utilizó el software MPlus 4.21, el cual permite la estimación de
modelos con varias variables dependientes e independientes, provee
índices de ajuste y es flexible a la hora de establecer restricciones causales.
Además, admite la inclusión de variables latentes.
La
Tabla 1 muestra los resultados de los diferentes modelos estimados, comenzando
por los modelos más simples AR y LT, siguiendo por añadir las
covariables a esos modelos, y finalizando por la implementación del modelo
ALT y su correspondiente extensión con las covariables. La sintaxis de
programación en MPlus de esos modelos puede pedirse al autor de este
estudio y la especificación gráfica de las relaciones entre las
variables puede consultarse en el Apéndice 1.
Tabla
1.
Resultados de los modelos estimados
|
Modelo |
Chi2 (gl) |
p-valor* |
R2 y1 |
R2 y2 |
R2 y3 |
R2 y4 |
|
AR |
0,98 (3) |
0,806 |
- |
0,429 |
0,531 |
0,583 |
|
AR_Cov |
2,72 (3) |
0,437 |
0,053 |
0,448 |
0,561 |
0,614 |
|
Cambio en R2 |
|
|
0,053 |
0,019 |
0,030 |
0,031 |
|
LT |
627,8 (5) |
<0,001 |
|
|
|
|
|
LT_Cov |
801,7 (10) |
<0,001 |
|
|
|
|
|
ALT** |
1,45 (2) |
0,482 |
- |
0,467 |
0,564 |
0,609 |
|
ALT_Cov** |
3,03 (5) |
0,694 |
0,053 |
0,464 |
0,573 |
0,625 |
|
Cambio en R2 |
|
|
0,053 |
-0,003 |
0,009 |
0,016 |
*Valores no significativos favorecen la hipótesis
nula, es decir, el ajuste del modelo. Cuando el modelo no se ajusta no se deben
interpretar los parámetros estimados, por eso no se indica el R2
** Modelos estimados con la varianza del
factor de crecimiento fijada a cero, en aras de mantener a la matriz de
covarianzas de las variables latentes definida positiva
Como
indica la Tabla 1, tanto el modelo AR como su extensión con covariables
obtienen un adecuado ajuste a los datos empíricos (p=0,806 y p=0,437,
respectivamente). Sin embargo, los modelos LT no se ajustan, por lo que la
modelización de las trayectorias individuales de los partidos no refleja
correctamente el patrón temporal de cambio en el resultado, algo que
sí hacen los modelos AR, de lo que se deriva que existe una alta
dependencia del estado anterior, a la hora de determinarse el resultado del
partido en el estado posterior.
Sin
embargo, los modelos ALT también se ajustan, una vez que la varianza de
la pendiente de la curva de trayectoria es fijada a cero. Esta
restricción no es demasiado problemática, y se ha realizado en
otras estimaciones de modelos similares, como la realizada por Morin et al.
(2011). En este caso, se ha utilizado esa fijación de la varianza por
los problemas de convergencia de la estimación, que como se ha indicado,
suele surgir con más profusión a medida que los modelos se
complican en tamaño. El efecto de las covariables sobre las
endógenas del modelo es dispar; la diferencia de calidad entre los equipos
(x1) siempre tiene un efecto significativo sobre las variables en todos los
modelos, mientras que el factor de calidad del partido (x2) no. De hecho los
modelos fueron reestimados obviando la variable x2, y los resultados fueron
prácticamente idénticos en relación al ajuste y a la
capacidad explicativa.
Por
tanto, globalmente, lo que se deriva de la estimación de esos seis
modelos es que el patrón de cambio es altamente dependiente del estado
anterior y que la única covariable influyente es la diferencia de
potencial entre los equipos, aunque su capacidad explicativa es pequeña.
Así, y como muestra el
cambio en el R2, la adición de las covariables no incrementa
ostensiblemente la varianza explicada, una vez controlado por el resultado en
el cuarto anterior. Además, la mayor variación se obtiene en el
primer cuarto, según el modelo AR_cov, y también el ALT_cov. La
diferencia entre ambos modelos radica en que el segundo modela también
las diferencias individuales de los partidos en el factor intercept, es decir, en el estado inicial del primer periodo
temporal (cuando la pendiente es 0). Como también se ha fijado la
varianza de esa pendiente a cero, entonces la variabilidad intra-partido se
considera homogénea en cuanto a la pendiente de la recta de trayectoria,
es decir, las únicas diferencias provienen de dónde comienza esa
recta (intercept).
Una
vez entendido el modelo que rige los datos empíricos, y donde se ha
mostrado que la diferencia de potencial entre los equipos influye de manera
más importante en el resultado del primer cuarto que en el cambio de
resultados entre los cuartos posteriores, se ha procedido a implementar un
modelo que explícitamente indique el efecto del resultado en ese primer
cuarto sobre la probabilidad de victoria. Para ello, se ha implementado un
modelo path de regresión
logística (ver Muthén y Muthén, 2008), donde se incluye la
diferencia de potencial entre los equipos (x1) como variable exógena,
cuya estimación de coeficientes se muestra en la Tabla 2 y especificación
gráfica en el Apéndice 2.
Tabla 2. Resultado del
modelo path de regresión
logística. Estimación de los coeficientes.
|
|
x1 |
y1 |
Intercept |
Casos clasificados
correctamente |
|
y1 |
7,706* |
|
1,153* |
|
|
y5 |
4,197* |
0,081* |
0.496* |
71,64%** |
*p<0,05
** Mejora
de 5% del porcentaje de clasificación de casos correctos con respecto a
un modelo que no incluya la covariable x1, y del 10% con respecto al modelo
base, sin variables independientes.
Nota: el valor de probabilidad de la
chi-cuadrado de los test de Pearson (0,76) y Hosmer-Lemeshow (0,28) es no
significativo, lo que apoya el ajuste del modelo.
Como
era de esperar tras la estimación de los modelos mostrados en la Tabla
1, y aunque ahora la variable de respuesta no es el resultado final del partido
cuantificado en diferencia de puntos, sino categorizado en victoria o derrota,
los coeficientes son significativos. De interés resulta, por tanto,
conocer los efectos marginales del resultado en el primer cuarto y la
diferencia de potencial sobre la probabilidad de victoria. La Figura 1, muestra
diferentes curvas de probabilidad en función de diversos valores para la
diferencia de puntos (entre -20 y 20), y de diferencia de potencial (entre -0,3
y 0,3). La línea roja marca el umbral de probabilidad a partir del cual
el caso se clasifica como victoria.
Figura
1.
Curvas de probabilidad de conseguir la victoria en función de la
diferencia en el marcador en el primero cuarto y de la diferencia de potencial
entre ambos equipos
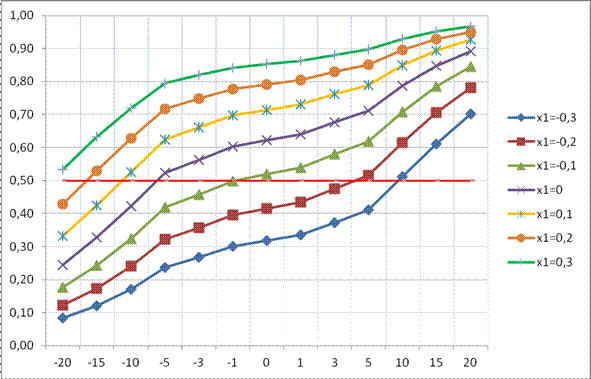
Nota: Curvas de probabilidad
para diferentes valores de diferencia de potencial entre equipos (x1), en
función de la diferencia en el marcador en el primer cuarto (eje X). El
equipo de casa se toma como referencia, por lo que valores negativos en el eje
X reflejan que el equipo local va perdiendo al finalizar el primer cuarto.
Estas son las curvas de proabilidad para el equipo local; para obtener las del
equipo visitante basta con realizar el simple cálculo: 1-Prob victoria
equipo local.
Teniendo
en cuenta que todos los datos se han tomado considerando como referencia al
equipo local, la interpretación de la Figura 1 es clara. Así, por
ejemplo, para partidos donde la calidad de los equipos es similar (x1=0), cuando
el marcador llega empatado al primer cuarto, el equipo local tiene más
del 60% de probabilidad de ganar. Y esa probabilidad sigue estando por encima
del 50% aunque vaya perdiendo hasta por 5 puntos. Para casos en los que la
diferencia de potencial entre el equipo de casa y el foráneo es
más evidente (x=0,2), ir perdiendo hasta de 15 puntos en el primer
cuarto no es sinónimo de probabilidad más alta de perder frente a
ganar. En el caso contrario (x=-0,2), cuando el equipo visitante es más
potente que el local, ese umbral se sitúa en los 5 puntos. Esa
influencia del factor cancha es más evidente si cabe a medida que la
diferencia de calidad entre los equipos se incrementa.
Pero
de más interés resulta aún si cabe el análisis de
los cambios en la probabilidad de victoria, a través de los efectos
marginales derivados del modelo logit. Así, cuando el equipo local es
más potente que el visitante (x1>0), la pendiente de la curva es
mucho más pronunciada en el tramo de resultados negativos (sobre todo
hasta los -5 y -3 puntos) que en
los positivos. Sin embargo, cuando el equipo visitante es el más potente
a priori (x1<0), la forma de las curvas es ligeramente distinta, y existe
más simetría entre los extremos de éstas.
4.
DISCUSIÓN Y CONCLUSIONES
Esta
investigación ha tratado de
esclarecer la influencia que tiene el resultado en el primer cuarto de un
partido de baloncesto sobre el marcador final, con el fin de detectar
precozmente situaciones problemáticas para los equipos. A través
de la implementación de varios modelos estadísticos basados en la
modelización del patrón temporal de resultados parciales, se
pueden discutir las contribuciones más relevantes de este estudio de la
manera siguiente:
En
primer lugar, los datos se explican mejor a través de modelos que
incluyan factores autorregresivos, es decir, donde el estado en un momento del
tiempo depende del estado anterior. La influencia de covariables que ayuden a
explicar la variación en esos estados temporales es sólo
significativa para el caso de la diferencia de potencial entre los equipos.
Esta variable añade explicación a las variables dependientes pero
su efecto es del orden de 4 veces menor que el efecto producido por el
resultado parcial en el estado temporal anterior. No obstante, la diferencia de
potencial entre equipos tiene su efecto más importante sobre el marcador
del primer cuarto del partido.
En
segundo lugar, el cambio producido por la evolución temporal del partido
puede considerarse invariable entre esos partidos, es decir, homogéneo,
siendo la única fuente de heterogeneidad el valor de la diferencia de
puntos. Así, las diferencias entre los partidos se explican mejor
considerando que la evolución es la misma para todos los partidos, con
la única diferencia del punto donde comienza esa diferencia, es decir,
del resultado en el primer cuarto.
En
tercer lugar, el factor cancha juega un papel fundamental en la
determinación del resultado final. Los equipos que juegan en casa pueden
permitirse ir perdiendo en el primer cuarto porque la probabilidad de ganar al
final del partido es mayor que la de perder. Así, cuando más
elevada es la diferencia de potencial entre los equipos mayor margen tiene el
equipo de casa para recuperar la desventaja en el marcador. No obstante, cuando
el equipo visitante es ostensiblemente más fuerte que el local, el
equipo local debe intentar ponerse por delante en ese primer cuarto.
En
cuarto lugar, la diferencia en las formas de las curvas de probabilidad indica
que el esfuerzo por recortar distancia en el marcador en el primer cuarto para
el equipo local tiene una mayor influencia en el cambio en la probabilidad de
victoria que el esfuerzo de alargar la diferencia en el marcador cuando
ésta es positiva. Sin embargo, cuando el equipo visitante es el más
potente a priori (x1<0), la forma de las curvas es diferente, y existe
más simetría entre los extremos de éstas, lo que indica
que tanto el esfuerzo por alargar la diferencia en el marcador como por
recortarla, trae incrementos similares en la probabilidad de victoria.
Por
tanto, y como conclusión final, se puede afirmar que es preferible
comenzar ganando, ya que la dependencia del estadio temporal anterior del
resultado de un partido de baloncesto es muy alta. Ir ganando en el primer
cuarto es fundamental para obtener la victoria en el partido, si bien ello
también depende, aunque en mucha menor medida, de si el equipo juega o
no en casa y de la diferencia de potencial entre los contendientes. Así,
para los equipos visitantes una ventaja de 10 o 15 puntos no “asegura”
la victoria al final del partido si el equipo local es más fuerte que
ellos, mientras que si el visitante es el más fuerte, entonces no debe
confiarse, ya que ventajas cortas del equipo local pueden ser irrecuperables.
Las
implicaciones para el juego del baloncesto a nivel estratégico o
táctico son claras. Así, los equipos deben considerar antes de
cada partido la diferencia de potencial entre los contendientes. Aunque este
estudio ha utilizado el valor del porcentaje de victorias al final de la temporada,
y ese es un dato que obviamente no se tiene antes de cada partido, los equipos
pueden utilizar el porcentaje de victorias actual como proxy a la diferencia de potencial real. Para ello, es recomendable
esperar a que la temporada haya avanzado un poco, para que ese dato sea
más fiable (Martínez, 2011). Una vez considerado el potencial
entre los equipos, parece recomendable que los equipos salgan “fuertes”
desde el principio, no reservando a jugadores importantes al comienzo del
encuentro, es decir, tienen que salir con la intención de abrir brecha
en el marcador lo antes posible, porque esa diferencia es ya muy difícil
de recuperar, sobre todo para el quipo visitante, incluso aunque éste
sea más fuerte que el local.
Por
tanto, si el equipo local es más fuerte que el visitante, debe de actuar
de diferente manera si, por ejemplo, a la mitad del primer cuarto tiene un
diferencial de -8 o de +8. Para el primer caso, debería de esforzarse
mucho más en recortar esa diferencia al final del primer cuarto que en
incrementar esa ventaja para el segundo caso, ya que el cambio en la
probabilidad de victoria por reducir el diferencial en, pongamos 4 puntos, es
relativamente mayor que en incrementar la ventaja 4 puntos más. Sin
embargo, cuando el equipo visitante es más fuerte, ambas estrategias
producen un efecto similar en el cambio de probabilidad de victoria. De este
modo, los entrenadores tendrían un criterio para manejar la
rotación de jugadores en ese primer cuarto, pudiendo tomar decisiones
relativas a dar descanso o no a sus jugadores clave.
Una de
las limitaciones de este estudio se refiere a la posible presencia del error de
medida en la variable que refleja la diferencia de potencial entre los equipos.
Como se ha indicado, antes de cada partido se obtiene una cifra que es una
aproximación al valor real. Dado que es bien conocido que el error de
medida atenúa la correlación entre las variables, sería de
esperar que el efecto real de la diferencia de potencial sobre los resultados
fuera un poco más relevante, aunque desde luego no cambiara de manera
importante los resultados mostrados.
Finalmente,
futuras investigaciones podrían profundizar en esta temática
considerando la distribución de minutos entre los jugadores de la
plantilla en cada cuarto, ya que ello permitiría controlar por las
decisiones tácticas que los entrenadores toman en relación al
reparto de tiempo de juego. Esos datos no están disponibles “en
bruto” en ninguna base de datos, por lo que habría que
registrarlos a través de los datos de jugada a jugada que webs como www.82games.com proveen. Si se consigue
realizar esa ardua labor para cada partido, entonces se podrían obtener
conclusiones más específicas sobre las variables que inciden en
el cambio de probabilidad de victoria en función de los marcadores
parciales del partido.
REFERENCIAS
BIBLIOGRÁFICAS
Arkes,
J. y Martínez, J. A. (2011). Finally, evidence
for a momentum effect in the NBA. Journal of Quantitative Analysis in Sports,
7 (3), Article 13.
Bollen, K. A. y Curran, P.J. (2004). Autoregressive
Latent Trajectory (ALT) models: A synthesis of two traditions. Sociological Methods and Research, 32,
336-383.
Brown,
M. y Sokol, J. (2010). An
improved LRMC method for NCAA basketball prediction. Journal of Quantitative Analysis in Sports,
6 (3), Article 4.
Caudill, S. B. y Godwin, N. H. (2002). Heterogeneous
skewness in binary choice models: predicting outcomes in the men's NCAA
basketball tournament. Journal of Applied
Statistics, 29 (7), 991-1001.
Cooper, H., DeNeve, K. M. y Mosteller, F. (1992).
Predicting professions sports game outcomes from intermediate game scores. Chance 5, 18–22.
Falk, B., Lidor, R., Lander, Y., y Lang, B. (2004),
Talent identification and early development of elite water-polo players: a
2-year follow-up study. Journal of Sports
Sciences, 22, 347-355.
Hayduk, L. A. (1996). LISREL Issues, Debates and Strategies.
Baltimore, MD: Johns Hopkins University Press.
Kline, R. B. (2011). Principles and practice of structural equation modeling (3rd ed.). New
York: Guilford Press
Lago,
C. y Casáis, L. (2010). La influencia de los resultados iniciales en la
clasificación final de los equipos de fútbol de alto nivel. Motricidad. European Journal of Human
Movement, 5(14), 107-122
Martínez,
J. A. (2011). El uso del porcentaje de victorias en modelos predictivos en la
NBA. Revista Internacional de Derecho y
Gestión del Deporte, 13.
Martínez,
J. A. (2012). Entrenador nuevo, ¿victoria segura? Evidencia en
baloncesto. Revista Internacional de
Medicina y Ciencias de la Actividad Física y el Deporte, 12 (48),
663-679.
Morin,
A. J. S., Maïano, C., Marsh, H. W., Janosz, M. y Nagengast, B. (2011). The
longitudinal interplay of adolescents’ self-esteem and body image: A
conditional autoregressive latent trajectory analysis. Multivariate Behavioral Research.
46, 157-201.
Muthén, L., y Muthén,
B.O. (2008). Mplus User’s Guide (5.1). Los Angeles, CA:
Muthén & Muthén.
Wilcox, R. R. (2010). Fundamentals of modern statistical methods.
Second Edition. New York: Springer.
Referencias totales / Total references: 14 (100%)
Referencias propias de la revista / Journal's own references: 1 (7,14%)
Rev.int.med.cienc.act.fís.deporte - vol. 14
- número 56 - ISSN: 1577-0354
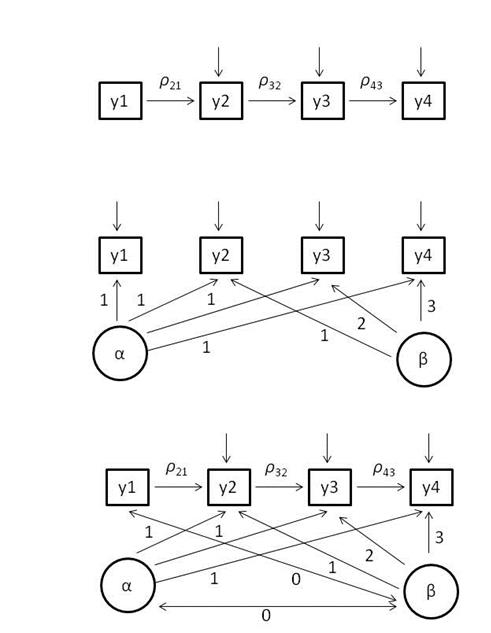
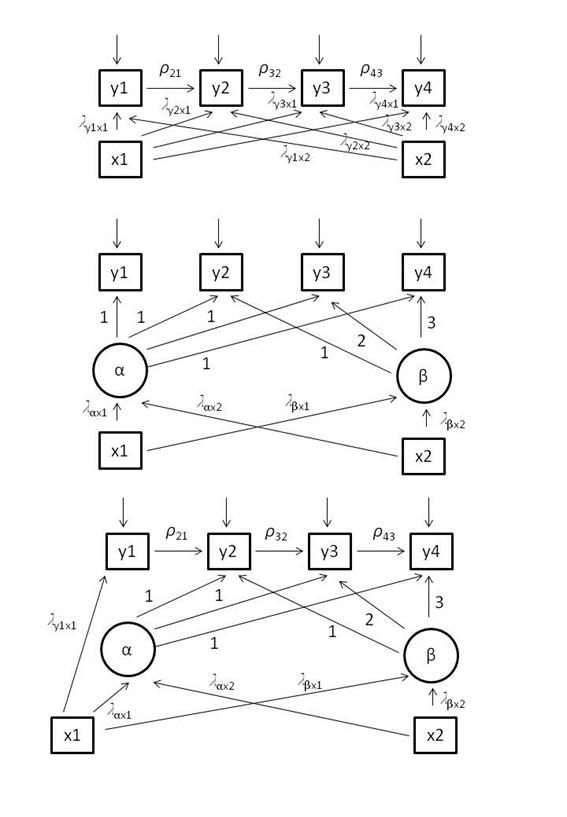
Apéndice
1
Esquema de los seis modelos testados en la
Tabla 1 (AR; LT; ALT; AR_cov;
LT_cov; ALT_cov). Se sigue la notación de Bollen y Curran (2004).
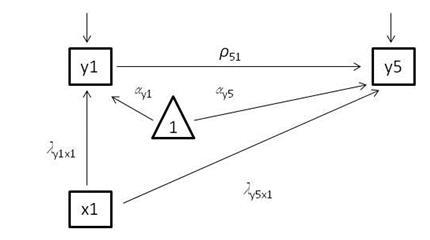
Apéndice 2: Esquema del modelo path logit. Basado
en la notación de Muthén y Muthén (2008) y Kline (2011).
Rev.int.med.cienc.act.fís.deporte - vol. 14
- número 56 - ISSN: 1577-0354