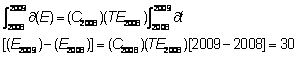Rev.int.med.cienc.act.fís.deporte- vol. 9 - número 36 - diciembre 2009 - ISSN: 1577-0354
Martínez, J.A. y Martínez, L. (2009). Gestión
de clientes de servicios deportivos; un modelo de dinámica de sistemas. Revista
Internacional de Medicina y Ciencias de
GESTIÓN DE CLIENTES DE SERVICIOS DEPORTIVOS; UN MODELO DE DINÁMICA
DE SISTEMAS
A CUSTOMER MANAGEMENT MODEL IN SPORTS
SERVICES; A SYSTEM DYNAMICS APPROACH
Martínez, J.A.1 y Martínez, L.2;
1 Profesor Ayudante. Departamento de Economía de
2 Profesora Contratada Doctora. Departamento de Economía de
CLASIFICACIÓN
UNESCO: 5311 “Marketing”
Recibido 8 enero 2009
Aceptado 13 de mayo
de 2009
RESUMEN
Esta
investigación propone un modelo general de gestión de clientes de servicios
deportivos que pretende mejorar la dirección estratégica de los mismos. Para
ello, se han integrado variables de la oferta y la demanda, en un planteamiento
principalmente enfocado en la perspectiva de marketing. La dinámica de sistemas
ha sido la metodología utilizada, con el fin de manejar la complejidad
inherente al estudio de este tipo de fenómenos. Además, el modelo se presenta
con un enfoque didáctico, en aras de facilitar su comprensión, describiendo las
ecuaciones, aportando la sintaxis de programación, y dejando las puertas
abiertas a la mejora y posible reformulación del mismo.
PALABRAS
CLAVES: gestión de clientes, gestión deportiva, dinámica de sistemas.
ABSTRACT
In this research a customer
management model of sports services is formulated. This model may serve as a
strategic tool that will allow managers to better understand the flow of
customers in the sports centre. System dynamics has been used in order to deal
with this complex task. The model is explained using a didactic approach. Finally,
the equations and the program syntax are provided.
KEYWORDS:
customer management, sport management, system
dynamics
INTRODUCCIÓN
La dirección
de servicios deportivos necesita modelos de gestión que permitan entender la
dinámica de un mercado cada vez más profesionalizado y competitivo. Y es que,
como indican Calabuig, Quintanilla y
Mundina (2008), el sector deportivo se ha desarrollado de forma muy importante
en los últimos años; así, entre 2002 y 2005 el número de empresas del sector servicios
en el campo de la actividad deportiva en España aumentó en un 27.82 %. Además,
en cifras económicas se pasó de un volumen de negocio de
En este contexto, la gestión de
clientes se muestra como un aspecto fundamental en la dirección de servicios
deportivos, tanto a nivel público como privado. De hecho, la literatura
académica especializada está actualmente mostrando gran interés en investigar acerca
de las actitudes de los consumidores y su comportamiento, proliferando los
estudios sobre satisfacción, calidad percibida y lealtad del consumidor (ej. Greenwell,
Brownlee, Jordan, y Popp, 2008; Mañas, Giménez, Muyor, Martínez-Tur y Moliner,
2008).
De particular
relevancia es el estudio de Martínez y Martínez (2009), donde estos autores
explican la dificultad del análisis de la lealtad del consumidor, proponiendo
la utilización de modelos dinámicos de simulación que permitan considerar la
complejidad de este fenómeno. Así, adoptando esta perspectiva metodológica, se
pueden considerar relaciones asimétricas, no lineales, recíprocas y dinámicas
entre las múltiples variables que forman los modelos de investigación; una
representación más acorde con la complejidad de los fenómenos sociales que los
tradicionales modelos econométricos usados en este ámbito de conocimiento.
Este
tipo de modelos de simulación cuentan con la ventaja añadida de su sencillo
manejo, no requiriéndose grandes habilidades matemáticas para su comprensión y
utilización. Además, permiten la simulación de distintos escenarios, por lo que
los gestores deportivos pueden simular diferentes hipótesis sobre cómo
evolucionarán ciertas variables en el futuro y qué efecto tendrán sobre las variables
clave del sistema, por ejemplo, sobre el número de clientes usuarios del
servicio.
Dadas
las bondades que ofrece la dinámica de
sistemas, el objetivo de esta investigación es proponer un modelo de gestión de
clientes de servicios deportivos que pueda servir como instrumento en la dirección
estratégica de los mismos. Lo haremos, además, de forma didáctica, con el fin
de facilitar su comprensión, aportando la sintaxis de programación, y dejando
las puertas abiertas a la mejora y posible reformulación del mismo. De este
modo, el modelo de esta investigación perfecciona y completa el propuesto por
Martínez y Martínez (2009).
La
dinámica de sistemas es una metodología para entender el cambio, usando
ecuaciones diferenciales. Está sustentada en la teoría de control y en la
teoría de dinámica no linear, y descansa sobre el pensamiento sistémico para
modelar un mundo complejo. El pensamiento sistémico es la capacidad para ver el
mundo como un sistema complejo, donde todo está conectado con todo, y donde el
todo es más que la suma de las partes.
Este enfoque permite aprender más rápida y efectivamente la estructura
de los sistemas, localizar los puntos clave y evitar la resistencia a
intervenciones. Además, contribuye a tomar decisiones consistentes con la mejor
decisión a largo plazo. Esta visión holística para estudiar los fenómenos facilita
la representación de modelos mentales sobre el problema que se está estudiando.
El objetivo es entender las causas estructurales que provocan el comportamiento
del sistema. A través de información cuantitativa y cualitativa el problema es
definido y más tarde es reflejado en un diagrama causal, el cual representa las
ecuaciones que relacionan las variables del modelo. Después se asignan valores
a determinados parámetros para que la simulación reproduzca los datos
históricos bajo condiciones plausibles. Si el modelo propuesto es coherente con
la situación presente y pasada, entonces se pueden simular el impacto de
diferentes políticas e intervenciones sobre el sistema, así como localizar los
puntos clave y realizar un análisis de sensibilidad. Existen excelentes
referencias sobre esta metodología, como por ejemplo: Sterman, (2001; 2002) o
Martín (2004).
La complejidad surge porque los
sistemas tienen importantes características (Sterman, 2001): (1) Los sistemas
están en constante cambio; (2) Los elementos de un sistema interactúan
fuertemente unos con otros, y con el mundo. Todo está conectado con todo; (3)
Existen vínculos de realimentación entre los elementos del sistema; (4) Las relaciones
entre elementos son casi siempre no lineales, por lo que el efecto raramente es
proporcional a la causa; (5) El sistema depende de la historia que tiene
detrás, es decir el comportamiento pasado influye en los resultados futuros;
(6) La dinámica del sistema surge espontáneamente de su estructura interna. A
menudo, pequeñas perturbaciones aleatorias son amplificadas y moldeadas por la
estructura de realimentación, generando patrones en el espacio y el tiempo.
Existen estados de auto-organización donde el comportamiento global emerge de
los vínculos entre los elementos individuales, produciendo comportamientos que
pueden distar mucho del comportamiento individual, e incluso pueden estar
libres de escala (se producen igualmente en pequeñas o grandes escalas); (7)
Las capacidades y comportamientos de los agentes en un sistema complejo cambia
en el tiempo. La evolución llega a la selección y proliferación de algunos
agentes, mientras que otros se extinguen. Se producen adaptaciones; (8) Existen
retardos temporales en las relaciones causales, por lo que la respuesta de un
sistema en el largo plazo es diferente de la respuesta a corto plazo; (9)
Debido a la complejidad del sistema, los puntos clave que provocan su
comportamiento son difíciles de detectar y a menudo son contra-intuitivos.
La
dinámica de sistemas es una metodología que supera a los métodos econométricos
tradicionales para entender ciertos problemas de marketing. Los diseños de
corte transversal son deficientes para estudiar los vínculos de realimentación
(Kaplan, Harik, y Hotchkiss, 2000; Kline, 2006). Los estudios longitudinales
son más adecuados, permiten considerar efectos autorregresivos, y los periodos
“lag” pueden ser observados en algunas situaciones. Sin embargo, cuando la
realidad no permanece estable, es decir, cuando hay uno o varios cambios en las
condiciones iniciales, los estudios longitudinales son más problemáticos
(Martín, 2004). Por ejemplo, podemos analizar un modelo de comportamiento del
consumidor en un mercado monopolístico usando un diseño longitudinal, pero
¿seguiría siendo ese modelo útil bajo un nuevo entorno competitivo? La dinámica
de sistemas permite una gran flexibilidad en simular distintos escenarios y
situaciones hipotéticas muy diversas.
La
principal ventaja de la dinámica de sistemas frente a otras técnicas
estadísticas que habitualmente manejan diagramas causa-efecto, como los modelos
de ecuaciones estructurales, es la flexibilidad para manejar relaciones asimétricas
y no lineales, el establecimiento de relaciones con operadores lógicos entre
las variables, o la posibilidad de establecer retrasos temporales y vínculos de
realimentación. No obstante, pueden existir dificultades en asignar los valores
adecuados a determinadas variables, cuando no se dispone de información
suficiente (investigaciones anteriores, alta experiencia en el campo bajo
estudio). Por ello, los modelos propuestos con este tipo de metodología deben
basarse en un alto conocimiento del problema en cuestión, y deben ser flexibles
y adaptables. Es decir, el modelo debe ser capaz de evolucionar, e incorporar
nueva información que permita mejorar las proyecciones realizadas.
En la
literatura sobre gestión deportiva, no hemos encontrado evidencias
significativas de la aplicación de la dinámica de sistemas desde el trabajo de
Haywood-Farmer, Sharman y Weinbrecht (1988). Tan sólo la reciente investigación
de Martínez y Martínez (2009), muestra empíricamente las capacidades de esta
metodología para ayudar en la gestión estratégica de los centros deportivos, especialmente
en la gestión de clientes.
Sin
embargo, el modelo de Martínez y Martínez (2009) puede reformularse, extenderse y completarse
para tener en cuenta un número mayor de variables que reflejen la complejidad
del fenómeno en cuestión. Es por ello, que presentamos un modelo más complejo,
y que, al mismo tiempo, puede resultar de mayor utilidad.
2. 1. Un ejemplo de modelo dinámico
Antes de revelar el modelo propuesto en esta
investigación, creemos conveniente explicar en un ejemplo muy simple cómo
funcionan estos modelos de simulación. Para ello, hemos utilizado el clásico
esquema del programa Vensim, especialmente recomendable para operar con
dinámica de sistemas.
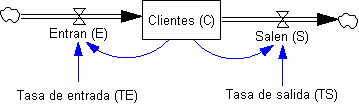
En ![]() ), pretendemos
saber cómo evolucionará el número de clientes hasta el año 2012, bajo el
supuesto de que la tasa de entrada y de salida son constantes (0.3 y 0.1,
respectivamente), es decir,
), pretendemos
saber cómo evolucionará el número de clientes hasta el año 2012, bajo el
supuesto de que la tasa de entrada y de salida son constantes (0.3 y 0.1,
respectivamente), es decir, ![]() y
y ![]() , tasas que
representan el porcentaje de clientes que entra y sale cada año (30% y 10%).
Como puede vislumbrarse, este modelo simple es poco realista, ya que no
contempla las posibles variaciones en las entradas y salidas de clientes, ni
tampoco dice nada sobre las causas acerca de por qué entran clientes y por qué
salen. Sin embargo, insistimos en que es un buen ejemplo para ilustrar el
funcionamiento de las ecuaciones.
, tasas que
representan el porcentaje de clientes que entra y sale cada año (30% y 10%).
Como puede vislumbrarse, este modelo simple es poco realista, ya que no
contempla las posibles variaciones en las entradas y salidas de clientes, ni
tampoco dice nada sobre las causas acerca de por qué entran clientes y por qué
salen. Sin embargo, insistimos en que es un buen ejemplo para ilustrar el
funcionamiento de las ecuaciones.
Figura 1. Ejemplo de modelo de simulación
|
|
Tabla 1. Resultados
de la simulación
|
Año |
(E) |
(S) |
(C) |
(TE) |
(TS) |
|
2008 |
30 |
10 |
100 |
0.3 |
0.1 |
|
2009 |
36 |
12 |
120 |
0.3 |
0.1 |
|
2010 |
43 |
14 |
144 |
0.3 |
0.1 |
|
2011 |
52 |
17 |
173 |
0.3 |
0.1 |
|
2012 |
62 |
21 |
207 |
0.3 |
0.1 |
Las
ecuaciones que rigen el sistema son las siguientes (Ecuación 1):
Ecuación 1.
|
|
Integrando
entre dos momentos del tiempo consecutivos, y teniendo en cuenta los valores
iniciales de entrada anteriormente descritos, se pueden obtener los valores de
las variables, tal y como muestra la Ecuación 2.
Ecuación 2.
|
|
Por
tanto, en el primer periodo de tiempo se hacen 30 nuevos clientes.
Análogamente, se obtiene el valor de los clientes que abandonan: 10. Así, en
2009 habrá 120 clientes, y se pueden ir calculando sucesivamente el resto de
valores de las variables.
Es
evidente que el cálculo manual de la simulación se complica enormemente a
medida que el modelo se hace más complejo. Es por ello, que los programas de
software específico son necesarios. En esta investigación utilizaremos el
programa Vensim PLE Plus 5.5d, una de las versiones del programa más expandido
en este tipo de metodologías. Una versión gratuita del mismo puede obtenerse
en: http://www.vensim.com/freedownload.html,
con lo que todos los esquemas y programación del modelo propuesto en este
artículo, pueden ser reproducidos fácilmente por los lectores.
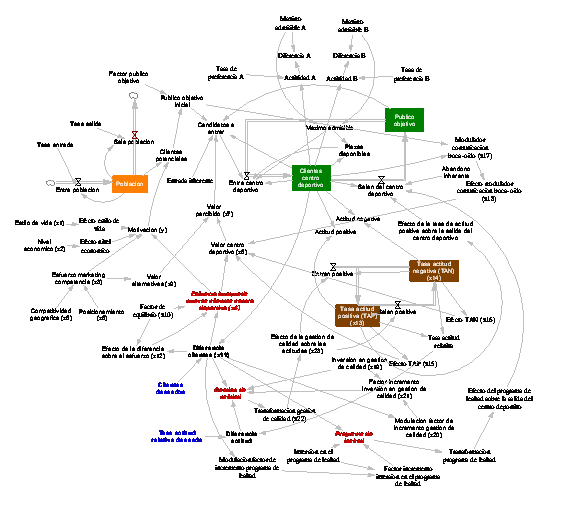
MODELO DE GESTIÓN DE CLIENTES DE
SERVICIOS DEPORTIVOS
El
modelo propuesto se muestra en
Un principio
fundamental en la dirección estratégica de marketing es la determinación del
público objetivo, es decir, aquellos consumidores a los que va dirigida la
oferta de servicios. En el caso de los servicios deportivos, el público
objetivo es una parte de los consumidores potenciales de esos servicios, entendiendo
a los consumidores potenciales como la fracción de población total que está
motivada para la práctica deportiva. Así, por ejemplo, un centro de fitness exclusivo para mujeres, tendrá
como consumidores potenciales a todas las mujeres de la población motivadas
para hacer deporte, y como público objetivo a aquellas mujeres motivadas que
tengan unas características determinadas (rango de edad, etc.). Al mismo
tiempo, los servicios deportivos municipales seguramente tendrán como público
objetivo un porcentaje de población similar a los clientes potenciales, ya que
los servicios públicos diseñan una oferta orientada a prácticamente todos los
segmentos de población.
Por tanto, se debe modelar el flujo poblacional (a
través de las estadísticas del INE, por ejemplo), determinar el porcentaje de
personas motivadas para hacer deporte y establecer las características del
público objetivo, siendo esta última labor, una decisión estratégica de los
gestores deportivos.
Figura 2. Modelo dinámico de gestión de clientes
|
|
La determinación del valor de la variable motivación
es una de las tareas más complicadas en este modelo. Básicamente, es análogo a
la estimación de la probabilidad de consumo deportivo, es decir, de la demanda.
Existen múltiples formas de obtener esa información. Para ello, es necesario
especificar un modelo (indicando las variables relevantes que afectan a la
motivación y su forma funcional) y estimarlo. Una introducción a esta forma de
proceder puede encontrarse en Wooldridge (2006).
García Ferrando (2006), en su estudio sobre hábitos
deportivos en España referente al año 2005, muestra que más del 50% de la
población española está interesado en la práctica deportiva, por lo que podemos
considerar que ese porcentaje de individuos está motivado para el consumo de
servicios deportivos. Sin embargo, no conocemos ningún estudio econométrico que
haya analizado la función de demanda para estudiar los factores que afectan a
esa motivación y la importancia de estos. No obstante, en nuestro modelo hemos
especificado 4 elementos fundamentales: estilo de vida (x1), nivel económico (x2), esfuerzo de marketing de la competencia (x3) y esfuerzo de búsqueda de
nuevos clientes del centro deportivo (x4).
El estilo de vida, hace referencia a los hábitos generales de la población,
englobando factores como la afición por el deporte, el cuidado de la salud o el
tiempo dedicado al ocio. Es obvio que actualmente, a nivel global, estos
factores tienen una tendencia alcista en la sociedad, por lo que la motivación
para practicar deporte se ve favorecida. El nivel económico considera la
restricción presupuestaria de los individuos. El consumo de servicios
deportivos supone un coste, por lo que se asume que la motivación se produce si
el individuo puede económicamente hacer frente al pago de esos servicios. Los
esfuerzos de marketing de las organizaciones deportivas del municipio influyen
también en esa motivación, incitando al consumo en la medida en que se
intensifica su inversión. Finalmente, pueden existir otros factores (u) que también afectan a la motivación
para el consumo (y), al margen de los
cuatro descritos, y que deben ser tenidos en cuenta en el modelo a través de
una perturbación aleatoria. La ecuación del modelo es entonces la siguiente:
Ecuación
3.
|
|
La forma en la que se combinan esas cuatro variables
debe ser especificada por el investigador, y la estimación de la importancia
(β) de cada una de ellas puede ser derivada empíricamente a través de
estudios de mercado. Una opción sería la estimación de un modelo de regresión
logística, que es lineal en los parámetros, como muestra la Ecuación 4.
Ecuación
4.
|
|
Si no se
disponen de datos de mercado, lo más aconsejable es que el propio investigador
asigne directamente los valores de importancia, en base a su experiencia y
conocimientos. Se trata de especificar una ecuación determinista de naturaleza
simple (lineal) o más compleja (no lineal), estableciendo el rango de valores
posibles para las variables.
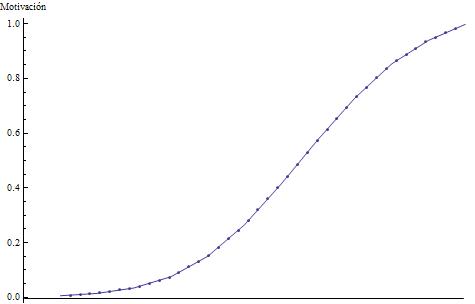
Nos hemos decantado por una ecuación no lineal de
acuerdo con el siguiente razonamiento: La relación entre las variables
independientes (inputs) y la variable dependiente (output) ha de ser
equivalente a una curva en forma de S,
es decir, donde haya no linealidad importante en los extremos. Eso quiere decir
que en un rango de valores bajo de inputs obtendremos prácticamente el mismo
valor de motivación (muy bajo), al igual que para un rango de valores alto (en
este caso, muy alto). La forma de esta curva es similar a otras utilizadas en
la especificación de este tipo de efectos (ej. Mittal, Ross y Baldasare, 1998)
y la ecuación que proponemos para caracterizarla es la siguiente:
Ecuación
5.
|
|
Esta ecuación indica que cuando el estilo de vida, el
nivel económico, o ambos tiene un valor mínimo, la motivación es prácticamente
cero, ya que, independientemente de los esfuerzos de marketing, el consumidor
no tiene ningún tipo de afición, necesidad o capacidad económica para consumir
este tipo de servicios. Sin embargo, cuando esas dos variables tienen un alto
valor, el consumidor está tan motivado que le afectan muy poco los esfuerzos de
marketing de las empresas, ya que tiene la necesidad imperiosa de consumir
prácticamente sin restricción presupuestaria.
Es por ello, que x3
y x4 contribuyen mínimamente
en esas situaciones, siendo, sin embargo, su contribución relativa mucho más
importante en la parte más lineal de la curva, es decir, cuando obtenemos
valores intermedios de x1 y x2.
Consideramos entonces que la motivación es una
variable acotada en un intervalo [0,1], representando en tanto por uno el
número de individuos que quieren consumir servicios deportivos. Las variables x1 y x2 están acotadas entre -3 y +3, mientras que x3 y x4 lo están en el intervalo [0,1]. Estas escalas son
arbitrarias, pero el rango de valores que representan está justificado por el
ajuste de la variable output en el rango especificado. Las variables “efecto
esfuerzo de marketing competencia” y “efecto esfuerzo búsqueda nuevos clientes
centro deportivo” simplemente retratan la función exponencial. La forma de la
curva puede verse en
Figura 3. Motivación por practicar deporte en
función de las variables consideradas
|
|
El esfuerzo de marketing de la competencia dependerá
principalmente de dos factores: competitividad geográfica (x5) y posicionamiento (x6). El factor geográfico es un elemento determinante en
la elección de un centro deportivo. Por ejemplo, Martínez y Martínez (2008)
encuentran que alrededor del 33% de usuarios afirma como principal razón para
la elección de su centro deportivo la cercanía. Por su parte, el
posicionamiento es un concepto clave en marketing, y hace referencia al lugar
que ocupa el centro deportivo en la mente del consumidor en relación con los
demás centros competidores. De esta forma, podemos establecer una variable que
indique en qué medida el centro en cuestión tiene un posicionamiento
diferenciado, es decir, carácter de unicidad en la mente de los individuos.
Distinguimos la dimensión geográfica del resto que
pueden determinar el posicionamiento del centro deportivo porque si existe un
monopolio geográfico el centro deportivo no tiene necesidad de invertir en comunicación
de marketing. Sin embargo, cuando esto no es así, a nivel estratégico el centro
deportivo debe intentar conseguir monopolios mentales, es decir, una posición
única en la mente de los individuos. Para ello hace falta esfuerzo en
marketing, tanto para mantener esa posición única si ya se tiene, como para
intentar llegar a ella si no se tiene (diferenciarse). En este segundo caso, la
inversión seguramente será incluso mayor.
La ecuación que rige las relaciones entre esas
variables es la siguiente:
Ecuación
6.
|
|
Siendo x5
una variable acotada en un intervalo [0,1] y x6 en (0,1]. De esta forma, mayores niveles de
competitividad geográfica y de posicionamiento no diferenciado incrementarán
los valores de x5 y x6. Hay que notar que x6 nunca puede ser cero,
porque cuando no se tiene un monopolio geográfico el centro deportivo
necesariamente tiene que invertir en comunicación. La asignación de valores
para esas variables tiene que realizarla la dirección del centro deportivo.
Una vez establecido el público objetivo, los
candidatos a entrar al centro deportivo serán aquellos cuyo valor percibido en
el consumo del servicio sea mayor que el de las alternativas disponibles,
entendiendo esas alternativas como la oferta de servicios sustitutivos o
incluso la opción de no consumir. Este razonamiento proviene de la teoría de la
utilidad aleatoria desarrollada por Manski (1977), que indica que cuando el
consumidor tiene un conjunto de opciones de compra, elegirá la que le confiere
mayor utilidad o valor. Desde el punto de vista de marketing, interpretamos ese
valor percibido asumiendo que el consumidor no tiene por qué comportarse de
manera racional en su elección. No obstante, en la decisión final, lo que
subyace es una comparación entre el valor percibido de diferentes opciones,
independientemente de que los elementos que formen esa función de valor sean
objetivamente comparables.
De este modo el valor percibido (x7) es una variable [0,1] que
representa en tanto por uno, el número de personas del público objetivo
candidatos a entrar, es decir, aquellas personas cuyo valor percibido de elegir
el centro deportivo (x8) es mayor que el valor de las alternativas (x9). La cuestión ahora es identificar
las variables que determinan la variación de x8 y x9.
Como determinante de x9 hemos considerado únicamente el esfuerzo de marketing
de la competencia (x3). Y
es que esta variable asumimos que contiene información acerca de otros factores
que tradicionalmente se identifican con la determinación de las expectativas, y
por ende, del valor percibido, como son las experiencias pasadas y la
comunicación boca-oído (Parasuraman, Zeithaml y Berry, 1985). Es evidente que
si los consumidores han tenido buenas experiencias con otros servicios
deportivos, y además escuchan buenas referencias de ellos, se incrementará el
valor de elección de los mismos (x9).
Pero como la variable x3
está construida en base a la rivalidad competitiva, es perfectamente plausible
asumir que mayores niveles de x3,
es decir, mayor intensidad competitiva, incrementarán los valores de x9, ya que mayor
competitividad supone implícitamente que los rivales del centro deportivo
objeto de gestión están haciendo bien las cosas.
La variable x9
la hemos acotado en el intervalo [0,0.9], ya que suponemos que, incluso en el
caso más desfavorable para el centro deportivo (máxima rivalidad competitiva),
éste puede conseguir nuevos clientes si consigue obtener un valor de x8 superior a 0.9, como veremos
más adelante.
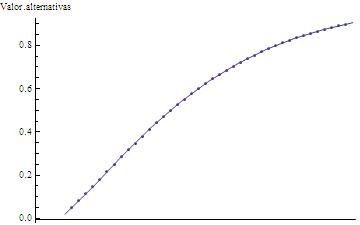
La relación entre x3 y x9
es de nuevo no lineal, decantándonos por la transformación half-logística,
como se muestra en la Ecuación 7, que nos permite obtener la forma de la curva
deseada para el rango de valores considerado.
Ecuación
7.
|
|
La forma de la función puede contemplarse en
Figura 4. Valor de las alternativas de elección en
función del esfuerzo de marketing de la competencia
|
|
Esta parte del modelo nos indica el número de
personas que entrarán como usuarios del centro en cada periodo de tiempo
considerado. Por tanto, entrarán aquellos individuos cuyo valor percibido
supere el de las alternativas. No obstante, ese número estará condicionado por
la cantidad de plazas que oferte el centro. De esta forma, son los gestores del
centro deportivo los que determinan la capacidad máxima del recinto, la cual
será normalmente la suma de la máxima capacidad para cada una de las
actividades. En este modelo, sólo hemos considerado dos actividades (A y B)
para no complicar demasiado la ilustración, pero la representación de un mayor
número de actividades es fácilmente reproducible. Las Tasas de preferencia A y
B representan el porcentaje de clientes que cursan cada actividad.
Hemos considerado la variable “entrada inherente”
como modulador de la entrada de clientes. Con ella nos referimos a una tasa de
entrada que se producirá todos los años al margen de las comparaciones sobre
valor percibido. Esta aparente contradicción queda justificada por el hecho de
que en la determinación de la elección del consumidor pueden actuar factores
que no se han tenido en cuenta en el modelo. Además, es necesario contar con
una variable que sirva como factor de ajuste a los datos históricos. De este
modo, se corrige una de las limitaciones del modelo, tal y como está
presentado, es decir, que si el valor de las alternativas es mayor que el del
centro deportivo no entre ningún cliente ese año. Esta situación podría
considerarse poco probable, ya que sería difícil imaginar un servicio deportivo
en el que durante un año no entrara ningún nuevo cliente. La modulación de esa
variable, la establece la dirección del centro, y tiene un significado similar
a la utilización que tiene en el modelo propuesto por Martínez y Martínez (2009).
Las personas que salen del centro deportivo, es
decir, que dejan de ser clientes usuarios de las actividades se convierten
automáticamente en público objetivo, ya que suponemos que siguen teniendo aún
alguna motivación para practicar deporte, y que la baja del centro se debe a
otros motivos, ya sea por insatisfacción o cambio en las preferencias del
cliente o por razones situaciones o contextuales (lesiones, cambio de
domicilio, etc.).
El siguiente paso es ilustrar en el modelo los
efectos que tienen el número de clientes y sus actitudes hacia el centro
deportivo sobre otras variables.
Los gestores deben plasmar en su planificación
estratégica el número de clientes deseado para cada periodo de tiempo, es
decir, en un horizonte temporal determinado. Ese número objetivo se confrontará
con los clientes reales, y la diferencia resultante servirá como indicador de
cumplimiento de esa meta estratégica. El número de clientes deseado no tiene
por qué coincidir con la máxima capacidad del centro, ya que es el gestor el
que debe planificar en qué medida se quiere crecer. En nuestro modelo, hemos
establecido esa diferencia como un ratio entre los clientes actuales y los
clientes deseados. Si esa diferencia es menor que la situación de equilibrio,
el centro deportivo implementará acciones de comunicación de marketing para
conseguir nuevos clientes. Esa situación de equilibrio (x10) la hemos establecido en un valor de 0.9, lo que
realmente sería “muy cercano” a la situación de completo equilibrio (es decir,
diferencia=1). De nuevo, cada gestor puede libremente fijar el valor de ese
ratio.
La relación entre el valor de desequilibrio (x11) y su efecto sobre el esfuerzo
económico en buscar nuevos clientes (x12)
es de nuevo no lineal, ya que es evidente que el esfuerzo a realizar cuando la
diferencia es pequeña no será proporcional a cuando haya un gran desequilibrio,
situación en la que se debe invertir de forma importante en comunicación de
marketing. Para ello hemos utilizado la siguiente ecuación:
Ecuación
8.
|
|
El esfuerzo realizado por el centro deportivo en la
búsqueda de nuevos clientes unido a la comunicación boca-oído recibida,
determinará el valor de elección del centro deportivo. La comunicación
boca-oído es reconocida como uno de los recursos de transmisión de la
información más influyente en la sociedad, jugando un papel preponderante en la
elección de compra del consumidor (Duan,
Gu, y Whinston, 2008), y se define como cualquier forma de comunicación no
formal entre consumidores (East, Hammond y Lomax, 2008). Las actitudes del
consumidor con respecto al servicio recibido son los principales determinantes
de esta variable (Mazzarol, Sweeney y Soutarm, 2007). Es decir, actitudes como
la satisfacción o la calidad percibida influyen en la forma en la que los
consumidores del centro deportivo van a hablar bien o mal de él. La naturaleza
de ese efecto también ha sido estudiada en la literatura, y aunque no existe
total uniformidad en los resultados de esos estudios, sí que puede asumirse que
de nuevo existe una relación no lineal, en forma de U (Anderson, 1998). Sin
embargo, creemos que la teoría de las perspectivas (Kahneman y Tversky, 1979) proporciona
sustento suficiente como para considerar que las emociones negativas producirán
un mayor efecto sobre el comportamiento que las positivas. De este modo los
efectos de las actitudes sobre la comunicación boca-oído seguirán teniendo
forma de U, pero de forma asimétrica, es decir, con una curva más suavizada en
la parte positiva.
Por tanto, las ecuaciones que especifican el efecto
de las actitudes positivas y negativas son las siguientes:
Ecuación
9.
|
|
siendo x13
y x14 las tasas de actitud
positiva y negativa, respectivamente, y x15 y x16 el valor transformado que indica su efecto sobre
otras variables. Evidentemente, para el efecto negativo hemos incorporado un
signo menos.
Llegados a este punto, ya hemos identificado y
definido las variables que determinan el valor del centro deportivo (x8), el cual ha de compararse
con el valor de las alternativas (x9),
como hemos indicado anteriormente. Recordamos que los determinantes de x8 son: el esfuerzo de
búsqueda de nuevos clientes del centro deportivo (x12), y la comunicación boca-oído positiva y negativa (x15 y x16, respectivamente). La forma en la que se relacionan
esas variables es ciertamente compleja. Por ejemplo, Day (1971) sostiene que la
comunicación boca-oído es nueve veces más efectiva que la publicidad
tradicional para influir sobre las actitudes de los consumidores. Por su parte,
Hogan, Lemon y Libai (2004), muestran
como la primera de ellas es tres veces más efectiva que la segunda. Existen
entonces indicios en la literatura para sostener que la comunicación entre
individuos tiene un efecto mayor sobre las actitudes y el comportamiento de
estos que la publicidad tradicional. Aunque, evidentemente los esfuerzos de
comunicación del centro deportivo no deben restringirse sólo a la publicidad,
sí que parece plausible suponer que el efecto de la comunicación boca-oído es
mayor, tal y como defienden Hogan, Lemon y Libai (2004). Además, se ha de tener
en cuenta el número de clientes del centro en relación al público objetivo
total. Es decir, es de esperar que la comunicación boca-oído sea más intensa y
efectiva a medida que el ratio (x17)
entre clientes y público objetivo aumenta. Utilizando la terminología del
marketing viral, se consigue una difusión más rápida de la información si el
número inicial de “infectados” (en este caso clientes) es mayor. De este modo,
vamos a suponer que la comunicación boca-oído será más efectiva cuando las
actitudes sean positivas y cuando el número de clientes del centro sea un
porcentaje determinado del público objetivo. Suponemos que si el ratio está
entre el 3 y el 5%, los efectos (x18) se maximizan. Hemos
escogido la forma de la función de distribución Weibull, ya que representa una
forma adecuada para nuestros propósitos cuando se cumple la siguiente ecuación:
Ecuación
10.
|
|
Por tanto, la ecuación que proponemos para
determinar el valor del centro deportivo es la siguiente:
Ecuación
11.
|
|
siendo a
un factor multiplicativo que transforma los valores de x12 a un intervalo [0,1]. Este factor depende de la
elección del factor de equilibrio x10.
En este caso, su valor es de 1,6.
Como se puede comprobar, x8 es máximo, es decir, igual a 1, cuando x12, x15 y x18
es máximo. Evidentemente si x15
es máximo, x16 es cero, ya
que ello ocurrirá si todos los consumidores del centro deportivo tienen una
actitud positiva.
Las actitudes de los clientes del servicio son, por
tanto, un elemento vital en la gestión del centro deportivo. Es por ello que
creemos que se debe realizar un seguimiento periódico a las mismas (a través de
cuestionarios, por ejemplo) y establecer objetivos referentes a su dirección.
Así lo hemos indicado en nuestro modelo, estipulando como meta una tasa de
actitud relativa determinada, que debe ser comparada con la tasa real (x13/x14).
Tenemos entonces dos objetivos claros de marketing
susceptibles de ser confrontados con la realidad: el número de clientes y sus
actitudes, es decir, una mezcla entre metas cuantitativas y cualitativas,
aunque esta última ha de “cuantificarse” mediante acciones de investigación. Ya
hemos explicado que cuando no se está en situación de equilibrio en ese primer
objetivo, se ha de invertir en comunicación de marketing, con el fin de atraer
nuevos clientes. Pero esa inversión no basta. La dirección del centro deportivo
necesita tener las herramientas suficientes para mejorar las actitudes del
consumidor, ya que éstas son vitales para la consecución de esos futuros
clientes, a través de la comunicación boca-oído. De ello ha de ocuparse el
sistema de gestión de calidad del centro.
La gestión de calidad es un elemento básico en
cualquier organización, independientemente de que se realice de forma más o
menos sistematizada, es decir, a través de la aplicación de normas (como
Suponemos en el modelo, por tanto, que el valor de
la inversión actual en gestión de calidad (x19)
lo establece la dirección, en un intervalo [0,1] representando en tanto por uno
el porcentaje de inversión sobre un máximo a fijar. Así, si actualmente se está
a tres cuartas partes de capacidad máxima, es decir, 0.75, se dispondrá de 0.25
unidades para invertir en situaciones de desequilibrio. A través de una modulación del factor de
incremento (x20), la
dirección del centro establece el factor de incremento de la inversión (x21):
Ecuación
12.
|
|
El efecto que tiene la inversión en gestión de
calidad (x23) sobre las
actitudes es no lineal, en forma de S. Nuevamente la forma de esa curva cobra
sentido, ya que es de esperar que pequeñas inversiones en calidad no produzcan
grandes resultados y que, a partir de un determinado nivel de inversión,
existan rendimientos marginales decrecientes. Para modelar ese efecto, hemos utilizado
la función sigmoide:
Ecuación
13.
|
|
siendo x22
la transformación del valor de la variable “gestión de calidad” a una escala
[-5,5]. Esta escala proporciona los valores adecuados para obtener la forma
deseada en S. El programa Vensim, permite fácilmente
realizar esa transformación a través de la construcción de una curva de
interpolación con los valores de entrada (ver Apéndice).
Finalmente, el modelo reproduce las causas del
abandono del servicio. Además del ya comentado abandono inherente, los
consumidores se irán en función de los efectos que produzcan sus actitudes y el
programa de lealtad implementado por el centro.
Como indican Yi y Jeon (2003), el objetivo de un
programa de lealtad es establecer un alto nivel de retención del consumidor, a
través de la mejora de su satisfacción y el incremento del valor percibido. Se
trata de aumentar los costes de cambio para el consumidor, de forma que
prefieran quedarse en el servicio. En este modelo, sin embargo, hemos separado
las actitudes del programa de lealtad, ya que asumimos que la variación de las
primeras vendrá principalmente determinada por la gestión de calidad del
centro. De este modo, incluimos dentro del programa de lealtad, aquellas
acciones encaminadas a incrementar el compromiso del consumidor con el centro,
como por ejemplo, creando un sentido de “comunidad” (Oliver, 1999). Así, una
acción posible dentro del programa de lealtad sería el fortalecimiento de los
vínculos sociales entre los consumidores del centro, creando una plataforma web
que facilite la comunicación entre ellos durante el año, especialmente en los
meses donde algunas actividades no se ofertan. Otro ejemplo sería la oferta de
promociones orientadas a mantener al consumidor a largo plazo, como descuentos
importantes por permanencia anual o bianual. Incluso la inversión en un sistema
informático de gestión de relaciones con clientes (CRM) quedaría encuadrada
dentro del programa de lealtad. Es por ello, que el centro deportivo necesita
destinar recursos a ese programa, siendo éstos determinados por la situación de
equilibrio en los objetivos. Es decir, un menor éxito en el cumplimiento de
objetivos, significará mayores inversiones en el programa de lealtad.
Hemos considerado el efecto de la tasa de actitud
positiva sobre la salida de clientes de la forma siguiente: la evidencia
empírica muestra que aunque los consumidores estén muy satisfechos con el
servicio y muestren su intención de continuar en él, muchos de ellos lo
abandonan (Martínez y Martínez, 2009). Es por ello, que hemos tomado los ratios
de conversión de Chandon, Morwitz y Reinart (2005), que relacionan las
intenciones del consumidor con el comportamiento efectivo real. Así, por
ejemplo, en una escala de muy probable a muy improbable, un 60% de consumidores que indiquen que “muy
probablemente” seguirán en el servicio realmente lo hará, un 20% de los que
indiquen que “probablemente” seguirán efectivamente lo harán, y así
sucesivamente (15, 10 y 8%). Para ello, hemos utilizado de nuevo una función de
interpolación (ver Apéndice).
Por último, el efecto del programa de lealtad ha
sido modelado utilizando exactamente el mismo razonamiento que el realizado
para modelar el efecto de la gestión de calidad, ya que ambos son sistemas de
gestión que necesitan una determinada inversión económica, y los efectos sobre
el sistema tendrán rendimientos marginales decrecientes a partir de un momento
dado.
4. FORMA DE PROCEDER Y ANÁLISIS DE
ESCENARIOS
La forma habitual de proceder con esta metodología
es la del sometimiento del modelo a dos tipos de evaluaciones.
La primera de ellas se refiere a la valoración de
los expertos sobre la idoneidad de la estructura de relaciones y ecuaciones
planteadas. Aunque creemos que el modelo está suficientemente sustentado sobre
la literatura descrita, son otros investigadores y profesionales de la gestión
deportiva los que deben terminar de perfilar, si es que así fuera necesario, el
modelo. Es por ello que ofrecemos la posibilidad de acceder a la sintaxis del
mismo, con el fin de evitar caer en el peligro de la “investigación de caja
negra”, y así facilitar la edición del modelo en el programa Vensim.
La segunda evaluación se refiere a confrontar las
predicciones del modelo con los datos históricos. Para ello, se necesita partir
de datos sobre flujo de clientes en un centro deportivo, plazas disponibles,
inversión en programas de calidad y lealtad, y datos de población (estos
últimos a través de estadísticas oficiales). El resto de variables que
funcionan como constantes en el modelo pueden ser “cualitativamente” fijadas
por el investigador o gestor, en base a sus conocimientos sobre el contexto de
estudio en cuestión. De este modo, y utilizando unos pocos datos reales de por
ejemplo 2 o 3 años anteriores, se puede analizar la bondad de ajuste del
modelo, teniendo la oportunidad de modular el valor de alguna constante.
Una vez realizados estos dos pasos, se debe realizar
un análisis de escenarios. Y es que los modelos de simulación dinámicos no
pretenden predecir exactamente el futuro, sino ofrecer una visión sobre cómo
evolucionará el sistema ante diferentes escenarios, es decir, cuando el valor
de ciertas constantes cambia,
además del establecimiento de criterios de elección entre políticas de gestión
diferentes Por ejemplo, ¿qué pasaría si
entrara un competidor muy fuerte en la ciudad dentro de 2 años?, o ¿cuál sería
la inversión necesaria en gestión de calidad o en programas de lealtad para
alcanzar un objetivo determinado de clientes en los próximos 5 años?.
Todos estos posibles escenarios pueden ser
analizados fácilmente utilizando la función STEP (ver por ejemplo la guía de
usuario del programa Vensim en http://www.catunesco.upc.edu/cursos/guia_vensim.htm).
5. CONCLUSIONES Y LIMITACIONES
El objetivo de esta investigación es la de
proporcionar un modelo útil de gestión de clientes de servicios deportivos, que
ayude a los directivos a mejorar la gestión de sus organizaciones. Basado en la
dinámica de sistemas, el modelo recoge las principales variables que
intervienen en la variación del flujo de clientes, definiendo las ecuaciones
que rigen esas relaciones. Además se puede estudiar cómo evolucionará el
sistema ante diferentes escenarios.
Este modelo puede ampliarse, retocarse y corregirse
en la medida de cada contexto de análisis, y una vez que el investigador o
gestor esté familiarizado con la metodología descrita. La flexibilidad es total,
aunque esas posibles variaciones, sobre todo si se realizan sobre ciertas
ecuaciones del modelo, deberán estar cimentadas sobre una base sólida de
literatura especializada.
Evidentemente el modelo tiene limitaciones. Creemos
que la más importante hace referencia a la no consideración de retardos
temporales. Las inversiones en gestión de calidad, programas de lealtad o
comunicación de marketing producen efectos diferidos en el tiempo, es decir, se
producen retrasos exponenciales en esos efectos, pudiendo ser palpables a lo
largo de varios periodos temporales. La modelización de esos efectos es
compleja. No obstante, creemos que si el modelo se utiliza programando periodos
de tiempo anuales, esos retrasos temporales tendrán menor importancia, ya que
un año es un plazo de tiempo suficientemente amplio como para que esas
inversiones produzcan resultados palpables en el siguiente periodo. Asimismo,
se podría incorporar cierto grado de aleatoriedad en algunas de las constantes
del sistema, a través de la utilización de funciones uniforme o normal (ver
Martínez y Martínez, 2009).
Pese a estas limitaciones, creemos que el modelo
propuesto puede servir como un “esqueleto” sólido sobre el que construir
modelos a medida para cada necesidad de investigación en este campo de la
gestión y marketing deportivo.
APÉNDICE
El modelo programado en Vensim puede ser descargado
en: www.upct.es/~beside
La sintaxis del modelo se muestra a continuación:
|
Abandono
inherente=0.05 |
|
Actitud
negativa=Clientes centro deportivo*"Tasa actitud negativa (TAN)
(x14)" |
|
Actitud
positiva=Clientes centro deportivo*"Tasa actitud positiva (TAP)
(x13)" |
|
Actividad
A=Clientes centro deportivo*Tasa de preferencia A |
|
Actividad
B=Clientes centro deportivo*Tasa de preferencia B |
|
Candidatos
a entrar= ((Publico objetivo+(Publico objetivo inicial-(Publico objetivo+Clientes
centro deportivo)))*"Valor percibido (x7)")+((Publico
objetivo+(Publico objetivo inicial-(Publico objetivo+Clientes centro
deportivo)))*Entrada inherente) |
|
Clientes
centro deportivo= INTEG (Entra centro deportivo-Salen del centro deportivo,500) |
|
Clientes
deseados=550 |
|
Clientes
potenciales=Población*"Motivación (y)" |
|
"Competitividad
geográfica (x5)"=0.5 |
|
Diferencia
A= Máximo admisible A-Actividad A |
|
Diferencia
B=Máximo admisible B-Actividad B |
|
"Diferencia
clientes (x11)"=Clientes centro deportivo/Clientes deseados |
|
"Efecto
de la diferencia sobre el esfuerzo (x12)"=(1/EXP("Diferencia
clientes (x11)"))-(1/EXP("Factor de equilibrio (x10)")) |
|
Efecto
de la tasa de actitud positiva sobre la salida del centro deportivo= WITH
LOOKUP ("Tasa actitud positiva (TAP) (x13)",([(0,0)-(1,0.8)],(0,0.08),(0.25,0.1),(0.5,0.15),(0.75,0.2),(1,0.6)
)) |
|
Efecto
del programa de lealtad sobre la salida del centro
deportivo=1/(1+EXP(-Transformación programa de lealtad)) |
|
Efecto
estilo de vida=1/(1+EXP( -"Estilo de vida (x1)")) |
|
"Efecto
modulador comunicación boca-oído (x18)"=1-EXP(-("Modulador
comunicación boca-oído (x17)"/0.2)^2) |
|
Efecto
nivel económico=1/(1+EXP( -"Nivel económico (x2)" )) |
|
"Efecto
TAN (x16)"=-("Tasa actitud negativa (TAN) (x14)"^2) |
|
"Efecto
TAP (x15)"=Tasa actitud positiva (TAP) (x13)"^3 |
|
Entra
centro deportivo=IF THEN ELSE(Clientes centro deportivo<Máximo admisible,
MIN(Candidatos a entrar, Plazas disponibles), 0) |
|
Entra
población=Población*Tasa entrada |
|
Entrada
inherente=0.0005 |
|
Entran
positiva="Tasa actitud negativa (TAN) (x14)"*"Efecto de la
gestión de calidad sobre las actitudes (x23)" |
|
"Esfuerzo
búsqueda nuevos clientes centro deportivo (x4)"=IF THEN ELSE(
"Diferencia clientes (x11)"<"Factor de equilibrio
(x10)", "Efecto de la diferencia sobre el esfuerzo (x12)", 0 ) |
|
"Esfuerzo
marketing competencia (x3)"="Competitividad geográfica
(x5)"*"Posicionamiento (x6)" |
|
"Estilo
de vida (x1)"=0.7 |
|
"Factor
de equilibrio (x10)"=0.9 |
|
Factor
incremento inversión en el programa de lealtad=(1-Inversión en el programa de
lealtad)/Modulación factor de incremento programa de lealtad |
|
"Factor
incremento inversión en gestión de calidad (x21)"=(1-"Inversión en
gestión de calidad (x19)")/"Modulación factor de incremento gestión
de calidad (x20)" |
|
Factor
público objetivo=0.5 |
|
Gestión
de calidad=IF THEN ELSE("Diferencia clientes (x11)"<0.9:OR:Diferencia
actitud<0.9,
"Inversión en gestión de calidad (x19)"+"Factor incremento
inversión en gestión de calidad (x21)" , "Inversión en gestión de
calidad (x19)") |
|
Inversión
en el programa de lealtad=0.5 |
|
"Inversión
en gestión de calidad (x19)"=0.75 |
|
Máximo
admisible=Máximo admisible A+Máximo admisible B |
|
Máximo
admisible A=400 |
|
Máximo
admisible B=200 |
|
"Modulación
factor de incremento gestión de calidad (x20)"=(1+"Diferencia
clientes (x11)")^2 |
|
Modulación
factor de incremento programa de lealtad=(1+"Diferencia clientes
(x11)")^2 |
|
"Modulador
comunicación boca-odo (x17)"=Clientes centro deportivo*10/Público
objetivo inicial |
|
"Motivación
(y)"=(Efecto estilo de vida*Efecto nivel económico)+((Efecto estilo de
vida*Efecto nivel económico)*(0.068*("Esfuerzo marketing competencia
(x3)"+"Esfuerzo búsqueda nuevos clientes centro deportivo
(x4)"))) |
|
"Nivel
económico (x2)"=1 |
|
Plazas
disponibles=Máximo admisible-Clientes centro deportivo |
|
Población=
INTEG (Entra población-Sale población,200000) |
|
"Posicionamiento
(x6)"=0.15 |
|
Programa
de lealtad=IF THEN ELSE("Diferencia clientes (x11)"<0.9,
Inversión en el programa de lealtad+Factor incremento inversión en el
programa de lealtad , Inversión en el programa de lealtad) |
|
Público
objetivo= INTEG (+Salen del centro deportivo-Entra centro deportivo, Publico
objetivo inicial-Clientes centro deportivo) |
|
Público
objetivo inicial=Clientes potenciales*Factor público objetivo |
|
Sale
población=Población*Tasa salida |
|
Salen
del centro deportivo=Clientes centro deportivo-(Clientes centro
deportivo*((Efecto de la tasa de actitud positiva sobre la salida del centro
deportivo+3*Efecto del programa de lealtad sobre la salida del centro
deportivo)/3.6))+(Clientes centro deportivo*Abandono inherente) |
|
Salen
positiva="Tasa actitud positiva (TAP) (x13)"*(1-"Efecto de la
gestión de calidad sobre las actitudes (x23)") |
|
"Tasa
actitud negativa (TAN) (x14)"= INTEG (+Salen positiva-Entran positiva,0.2) |
|
"Tasa
actitud positiva (TAP) (x13)"= INTEG (Entran positiva-Salen positiva,0.8) |
|
Tasa
actitud relativa="Tasa actitud postiva (TAP) (x13)"/"Tasa
actitud negativa (TAN) (x14)" |
|
Tasa
de preferencia A=0.5 |
|
Tasa
de preferencia B=0.5 |
|
Tasa
entrada=0.10 |
|
Tasa salida=0.08 |
|
"Transformación
gestión de calidad (x22)" = WITH LOOKUP (Gestión de
calidad,([(0,-6)-(10,10)],(0,-5),(0.1,-4),(0.2,-3),(0.3,-2),(0.4,-1),(0.5,0),(0.6,1),(0.7,2),(0.8,3),(0.9,4),(1,5)
)) |
|
Transformación
programa de lealtad= WITH LOOKUP (Programa de
lealtad,([(0,-6)-(10,10)],(0,-5),(0.1,-4),(0.2,-3),(0.3,-2),(0.4,-1),(0.5,0),(0.6,1),(0.7,2),(0.8,3),(0.9,4),(1,5)
)) |
|
"Valor
alternativas (x9)"= (1-EXP(-(3*"Esfuerzo marketing competencia
(x3)")))/(1+EXP( -(3*"Esfuerzo marketing competencia (x3)" ))) |
|
"Valor
centro deportivo (x8)"= (0.25*1.6*"Esfuerzo búsqueda nuevos clientes
centro deportivo (x4)")+0.75*(("Efecto TAP (x15)"+"Efecto
TAN (x16)")*"Efecto modulador comunicación boca-oído (x18)") |
|
"Valor
percibido (x7)"=IF THEN ELSE(("Valor centro deportivo
(x8)"-"Valor alternativas (x9)")>0, "Valor centro
deportivo (x8)"-"Valor alternativas (x9)", 0 ) |
En color rojo se
muestran los valores que tiene que aportar el investigador o gestor para
utilizar el modelo en cada contexto. Aquí se han reproducido con mero valor
ilustrativo.
En el modelo que aparece
en Vensim se han omitido los acentos para evitar incompatibilidades de lectura
entre diferentes versiones del programa.
REFERENCIAS
Calabuig, F.
Quintanilla, I., y Mundina, J. (2008). La calidad percibida de los servicios
deportivos: diferencias según instalación, género, edad y tipo de usuario en
servicios náuticos. Revista Internacional
de Ciencias del Deporte, 10(4), 25-43.
Chandon, P., Morwitz,
V. G. y Reinartz, W. J. (2005). Do Intentions Really Predict
Behaviour? Self-Generated Validity Effects in Survey Research?. Journal of Marketing, 69 (Abril), 1-14.
Day, G. S. (1971). Attitude change, media and word of mouth. Journal of Advertising Research, 11 (6),
31-40.
Duan, W., Gu, B. y Whinston, A. B. (2008). The dynamics of online
word-of-mouth and product sales—An empirical investigation of the movie
industry. Journal of Retailing, 84(2), 233-242
East, R., Hammond, K. y Lomax, W. (2008). Measuring the impact of
positive and negative word of mouth on brand purchase probability. International Journal of Research in
Marketing, 25, 215-224
García Ferrando, M. (2006). Postmodernidad y deporte: entre la
individualización y la masificación. Encuesta sobre hábitos deportivos de los
españoles 2005.
Madrid, C.S.D. y C.I.S.
Greenwell, C. T., Brownlee, E.,
Jordan, J. S. y Popp, N. (2008). Service fairness in spectator sport: the
importance of voice and choice on customer satisfaction. Sport
Marketing Quarterly,
17, 71-78
Haywood-Farmer. J.,
Sharman, O., y Weinbrecht, M. S.(1988). Using simple simulation models to
manage sports services. Journal of Sport Management,
2 (2), 118- 128
Hogan, J. E., Lemon, K. N. and Libai, B. (2004). Quantifying the ripple:
word of mouth and advertising effectiveness. Journal of Advertising Research, 44 (3), 271-280.
Kahneman, D., y
Tversky, A. (1979). Prospect theory: an analysis of decision under risk. Econometrica, 47 (2), 263- 291.
Kaplan, D., Harik, P.,
y Hotchkiss, L. (2000). Cross-sectional estimation of dynamic structural
equation models in disequilibrium. En R. Cudeck, S. H. C. du Toit, & D.
Sorbom (Eds.), Structural Equation
Modeling: Present and Future. A Festschrift in Honor of Karl G. Joreskog
(pp. 315-339). Lincolnville: Scientific Software International.
Kline, R. B. (2006).
Reverse arrow dynamics. En G. R. Hancock & R. O. Mueller (Eds.), A second course in structural equation
modeling (pp. 43-68). Greenwich, CT: Information Age Publishing.
Mañas, M. A., Giménez, G., Muyor, J. M., Martínez-Tur, V. y Moliner, C.
P. (2008). Los tangibles
como predictores de la satisfacción del usuario en servicios deportivos. Psicothema, 20 (2), 243-248
Manski, C. (1977). The structure of random utility models. Theory and Decision, 8, 229-254.
Martín, J. (2004). Sysware. La toma de decisiones
empresariales en un mundo complejo.
Martínez, J. A. y
Martínez, L. (2008). Calidad percibida, satisfacción y criterios de elección de
los consumidores de servicios deportivos públicos de Cartagena. Informe sin publicar.
Martínez, J. A. y
Martínez, L. (2009). Understanding customer loyalty through system dynamics;
the case of a public sports service in
Mazzarol, T., Sweeney, J. C. y Soutarm, G. N. (2007). Conceptualizing
word-of-mouth activity, triggers and conditions:an exploratory study. European Journal of Marketing, 41(11/12),
1475-1494.
Mittal, V., Ross W. T., y Baldasare, P .M. (1998). The asymmetric impact
of negative and positive attribute-level performance on overall satisfaction
and repurchase intentions, Journal of Marketing, 62(Enero), 33-47.
Oliver, R. L. (1999). Whence consumer loyalty?, Journal of Marketing, 63 (Número especial), 33-44.
Parasuraman, A.,
Zeithaml V. y Berry L. (1985). A conceptual model of service quality and its
implications for future research. Journal
of Marketing, 49, 35-48.
Sterman, J. (2001). System dynamics modeling: tools for learning in a
complex world.
Sterman, J. (2002). All models are wrong: reflections on becoming a
systems scientist. System Dynamics Review, 18 (4), 501-531.
Wooldridge, J. M.,
(2006). Introducción a
Yi, Y. y Jeon, H. (2003). Effects of loyalty programs on value
perception, program loyalty, and brand loyalty. Journal
of the
Rev.int.med.cienc.act.fís.deporte- vol. 9 - número 36 - diciembre 2009 - ISSN: 1577-0354