ECUACIÓN SIMPLIFICADA DE STEWART PARA VALORAR EL ESTADO ÁCIDO-BASE

Rev.int.med.cienc.act.fís.deporte- vol. 11 - número 41 - marzo 2011 - ISSN: 1577-0354

Peinado, A.B., Díaz, V.; Benito, P.J.; Álvarez, M. y Calderón, F.J. (2011). Simplificación de la ecuación de Stewart para valorar el estado ácido-base. Revista Internacional de Medicina y Ciencias de la Actividad Física y el Deporte vol. 10 (41) pp. 115-126. Http://cdeporte.rediris.es/revista/revista41/artecuacion197.htm

Texto en PDF

ORIGINAL

ECUACIÓN SIMPLIFICADA DE STEWART PARA VALORAR EL ESTADO ÁCIDO-BASE EN EJERCICIO

A SIMPLIFICATION OF THE STEWART EQUATION TO DETERMINE ACID-BASE STATUS IN EXERCISE

Peinado, A.B.¹, Díaz, V.²; Benito, P.J.³; Álvarez, M.⁴ y Calderón, F.J.⁵

¹Doctora en Ciencias de la Actividad Física y del Deporte. Profesora Ayudante Doctor, Facultad de Ciencias de la Actividad Física y del Deporte – INEF. Universidad Politécnica de Madrid, España (anabelen.peinado@upm.es).

²Doctor en Ciencias de la Actividad Física y del Deporte. Investigador postdoctoral, Facultad de Ciencias de la Actividad Física y del Deporte – INEF. Universidad Politécnica de Madrid, España (victor.diaz@upm.es). Instituto de Fisiología Veterinaria y Zurich Center for Integrative Human Physiology (ZIHP), Universidad de Zurich, Suiza.

³Doctor en Ciencias de la Actividad Física y del Deporte. Profesor Titular Interino, Facultad de Ciencias de la Actividad Física y del Deporte – INEF. Universidad Politécnica de Madrid, España (pedroj.benito@upm.es).

⁴Licenciada en Ciencias de la Actividad Física y del Deporte. Instituto de Fisiología Veterinaria y Zurich Center for Integrative Human Physiology (ZIHP), Universidad de Zurich, Suiza. (mariaalvarezsanchez@gmail.com).

⁵Doctor en Medicina y Cirugía. Profesor Titular de Universidad, Facultad de Ciencias de la Actividad Física y del Deporte – INEF. Universidad Politécnica de Madrid, España (franciscojavier.calderon@upm.es).

Código UNESCO: 2411 Fisiología Humana

Clasificación del Consejo de Europa: 13. Fisiología del deporte

Recibido 9 de septiembre de 2009

Aceptado 3 de noviembre de 2009

RESUMEN

El objetivo del estudio fue simplificar la ecuación de Stewart y verificar la validez de la ecuación propuesta. Veinticuatro varones realizaron un test a carga constante de 30 minutos en tapiz rodante. Fueron tomadas muestras de sangre capilar en reposo y en los minutos 10, 20 y 30 del test. Los parámetros ácido-base fueron analizados con un analizador de gases en sangre y el lactato por método enzimático. La [H⁺] fue calculada usando la ecuación de Stewart y la ecuación propuesta. La diferencia de medias entre la ecuación propuesta y la de Stewart fue de 0,004 nmol.L^-1 para la [H⁺]. Sin embargo, la diferencia de medias entre las ecuaciones y los valores medidos fue mayor de 8 nmol.L^-1 para la [H⁺] (p<0,001). La ecuación propuesta puede ser usada para estimar la [H⁺] en lugar de la ecuación de Stewart, aunque los valores estimados son significativamente diferentes a los valores medidos.

PALABRAS CLAVE: ion hidrógeno, diferencia de iones fuertes, equilibrio ácido-base, lactato, ejercicio a carga constante.

ABSTRACT

The aim of the present study was to simplify the Stewart equation and to test the validity of the proposed form. Twenty-four men performed a constant load exercise test for 30 min on a treadmill. Capillary blood samples were taken at rest, and again 10, 20 and 30 min into the test. Acid-base variables were measured using a blood-gas analyser and lactate levels were measured enzymatically. The [H⁺] was calculated using the Stewart equation: A[H⁺]⁴+B[H⁺]³+C[H⁺]²+D[H⁺]+E=0, and using a proposed, simplified version of this equation: A[H⁺]²+B[H⁺]+C=0. The difference in the mean [H⁺] results obtained with the two equations was 0.004 nmol·L^-1. However, the difference between the means of the equation-derived results and the measured values was highly significant at >8 nmol·L^-1 (p<0.001). The proposed equation can be used to estimate [H⁺] instead of the full Stewart equation, although the values obtained are significantly different to those actually measured.

KEY WORDS: acid-base equilibrium, constant load, hydrogen ion, lactate, strong ions.

1. INTRODUCCIÓN

La explicación tradicional del equilibrio ácido-base queda reflejada en la ecuación de Henderson-Hasselbach (1). De forma tradicional, el estado ácido-base del organismo se explica en términos cuantitativos mediante la relación entre pH plasmático e intensidad del ejercicio. Cuando la intensidad del ejercicio alcanza un valor determinado, el incremento de la concentración de ácidos en plasma determina un aumento de la concentración de protones ([H⁺]), con un descenso de la concentración de bicarbonato ([HCO₃^-]) (2). Sin embargo, esta explicación tradicional, aunque sencilla y de fácil compresión, tiene considerables limitaciones: en primer lugar, no tiene en cuenta las variaciones que se pueden producir individualmente en cada uno de los tres compartimentos afectados (intracelular, eritrocitario y plasmático), cuando aumenta la [H⁺]; en segundo lugar, no tiene en cuenta las relaciones entre los tres compartimentos, de manera que las variaciones en uno de ellos determinan cambios en los otros dos compartimentos.

Las variables independientes que determinan el equilibrio ácido-base de las soluciones biológicas son: la presión parcial de dióxido de carbono (PCO₂), la diferencia de iones fuertes ([SID]) (iones orgánicos e inorgánicos completamente disociados) y la concentración de ácidos débiles parcialmente disociados ([A_TOT]) (3-8). Los principales ácidos débiles que participan en esta variable son las proteínas y los fosfatos, siendo la albúmina y la globulina las proteínas más importantes (9). La influencia de estas tres variables en la [H⁺] puede ser determinada mediante ecuaciones matemáticas (Stewart y Fencl) (4), así como con el modelo simplificado del ion fuerte de Constable (10). Estas aproximaciones cuantitativas son usadas para explicar el estado ácido-base de soluciones simples y complejas, y ofrecen una novedosa visión de la fisiopatología de los desequilibrios ácido-base mixtos (1, 10, 11), siendo muy importante desde un punto de vista clínico. La ecuación propuesta por Stewart es una expresión polinómica de 4º grado: A[H⁺]⁴ + B[H⁺]³ + C[H⁺]² + D[H⁺] + E = 0 (3, 12) (ver material y métodos). Solucionar la ecuación de Stewart presenta la desventaja de tener que utilizar programas matemáticos cuyo uso es complejo. Debido a la escasa contribución de los coeficientes D y E es posible eliminar estos coeficientes. Además, la ecuación debe incluir sólo aquellos términos que sean importantes en la fenomenología del procedimiento (10). Por consiguiente, el objetivo de este estudio fue simplificar dicha ecuación y analizar la validez de la misma, comparando los valores de [H⁺] medidos con los estimados a través de las ecuaciones de Stewart y simplificada, de muestras de sangre capilar obtenidas durante un esfuerzo a carga constante.

2. MATERIAL Y MÉTODOS

2.1. SUJETOS

Veinticuatro varones sanos (26,7±4,9 años de edad; 176,1±6,3 cm de altura y 72,8±6,7 kg de peso corporal), estudiantes de Ciencias de la Actividad Física y del Deporte participaron en el estudio. Todos los sujetos estaban familiarizados con esfuerzos realizados en tapiz rodante y fueron informados de la naturaleza del estudio, dando su consentimiento por escrito. El estudio fue realizado según las directrices éticas dictadas en la declaración de Helsinki de la Asociación Médica Mundial, para la investigación con seres humanos.

2.2. PROTOCOLO

Todos los sujetos realizaron dos pruebas en tapiz rodante (H/P/COSMOS PULSAR 3P 4.0 ®, h/p/cosmos sports & medical, Nussdorf-Traunstein, Alemania). En la primera prueba se utilizó un protocolo incremental de 0,2 km·h^-1 cada 12 segundos y una pendiente fija de 1%. La segunda prueba consistió en una fase estable de 30 minutos, realizada a la carga correspondiente al punto medio de los umbrales ventilatorios (13-15) localizados en la primera prueba. La medición de la composición y el volumen del aire espirado se realizó con un equipo Jaeger Oxicon Pro ® (Erich Jaeger, Alemania).

2.3. MUESTRAS SANGUÍNEAS Y ANÁLISIS

Durante la prueba a carga constante se obtuvieron muestras de sangre capilar de la yema del dedo en: reposo, minutos 10, 20 y 30 de prueba. En total se obtuvieron 96 muestras sanguíneas. Las muestras fueron recogidas en capilares heparinizados de 100 µl (heparina equilibrada electrolíticamente). Una parte de la muestra (75 µl) se utilizó para el análisis de los parámetros ácido-base (pH, PCO₂, HCO₃^-) y de los electrolitos (Na⁺, K⁺, Ca²⁺y Cl^-). Para ello se utilizó un analizador de gases en sangre ABL 77 ® (Radiometer Copenhagen, Dinamarca). El resto de la muestra de sangre capilar (25 µl) se usó para medir la concentración de lactato ([Lac^-]) mediante método enzimático, utilizando el analizador YSI 1500 ® (Yellow Springs Instruments Co., USA). Ambos analizadores fueron calibrados antes de cada prueba. El analizador de lactato fue calibrado usando concentraciones conocidas de lactato de 5 y 15 mmol·L^-1. El analizador de gases en sangre se calibró automáticamente siguiendo las instrucciones del fabricante.

2.4. CÁLCULOS

Para calcular la [H⁺] se utilizó en primer lugar la ecuación de Stewart (3, 12):

Ecuación 1

A[H⁺]⁴ + B[H⁺]³ + C[H⁺]² + D[H⁺] + E = 0

donde A = 1, B = K_A + [SID], C = (K_A [SID] - [A_TOT]) - (K_c · PCO₂ + K_w^`), D = [K_A (K_C · PCO₂ + K_w^`) + (K₃ · K_C · PCO₂)] y E = K_A · K₃ · K_C· PCO₂. La [SID] fue calculada con los valores de electrolitos obtenidos con el analizador de gases en sangre y aplicando la siguiente fórmula: [SID] = ([Na⁺]+ [K⁺] + [Ca²⁺]) – ([Cl^-] + [Lac^-]) (4). Para la [A_TOT] se utilizó el valor medio obtenido por otros autores (18,2 mequiv·L^-1) (4, 5). K_A (3,0 x 10^-7 (equiv·L^-1)), K_C(2,46 x 10^-11 (equiv·L^-1)²/Torr), K₃ (6,0 x 10^-11 (equiv·L^-1)), K_w^`(4,4 x 10^-14 (equiv·L^-1)²), son las constantes de disociación de los ácidos débiles, del ácido carbónico, del bicarbonato y del agua, respectivamente. Los valores de estas constantes han sido utilizados anteriormente por otros autores (3-6, 12, 16). Para resolver la ecuación de Stewart se utilizó el programa Matlab v 7.1.0.246 (MathWorks, Inc. Natick, USA).

Posteriormente, la [H⁺] fue calculada con una ecuación de menor complejidad matemática obtenida a partir de la simplificación de la ecuación de Stewart. Debido a su probable escasa contribución en el resultado final, los coeficientes D y E fueron eliminados, obteniendo la siguiente ecuación:

Ecuación 2

A[H⁺]⁴ + B[H⁺]³ + C[H⁺]² = 0

Simplificando, la ecuación simplificada propuesta es:

A[H⁺]² + B[H⁺] + C = 0

2.5. ANÁLISIS ESTADÍSTICO

Para comparar los valores de pH y [H⁺] medidos por el analizador de gases en sangre y los valores estimados mediante la ecuación de Stewart y la ecuación simplificada propuesta, se realizó un análisis de la varianza (ANOVA) de una vía. Cuando se encontraron diferencias significativas se realizó un análisis post-hoc Scheffé. Para comprobar la validez de la ecuación simplificada se realizó un análisis de regresión lineal, se calculó la correlación de Pearson y se dibujaron los gráficos para las diferencias de las medias, siguiendo el procedimiento descrito por Bland y Altman (17), entre los valores de pH y de [H⁺] medidos, calculados con Stewart y con la ecuación propuesta. Para hallar la proporción de varianza explicada de la nueva ecuación se utilizó el coeficiente de determinación (r²). El análisis estadístico se llevó a cabo mediante el programa SPSS 12.0 para Windows (SPSS Worldwide Headquarters, Chicago, IL). El nivel de significación fue de α < 0,05.

3. RESULTADOS

Tabla 1. Datos descriptivos (media ± DE) para la [SID], PCO₂ y [Lac^-]. DE: Desviación estándar.
	[SID] (mequiv·L^-1)	[Lac^-] (mmol·L^-1)	PCO₂ (mmHg)
Reposo	39,1 ± 12,15	1,52 ± 0,53	36,21 ± 3,50
Min 10	32,64 ± 3,58	4,87 ± 2,09	35,79 ± 3,54
Min 20	33,5 ± 3,93	4,85 ± 1,97	31,88 ± 2,71
Min 30	34,42 ± 4,20	4,31 ± 2,08	30,92 ± 3,68

Los valores medios de pH y [H⁺] medidos obtuvieron diferencias significativas con los valores calculados por ambas ecuaciones, Stewart y la ecuación simplificada propuesta. Sin embargo, no hubo diferencias significativas entre los valores estimados por ambas ecuaciones.

La tabla 1 muestra los valores descriptivos (media ± DE) para la [SID], PCO₂ y [Lac^-], obtenidos con el analizador de gases en sangre y el analizador de lactato (ver material y métodos).

La tabla 2 muestra las medias ± DE del pH y la [H⁺] medidas, estimadas por la ecuación de Stewart y estimadas por la ecuación propuesta (ecuaciones 1 y 2 respectivamente).

Los diagramas de dispersión se muestran en la figura 1. Se obtuvo una alta correlación entre los valores de [H⁺] calculados con la ecuación de Stewart y con la ecuación simplificada (r = 0,999; p<0,001); sin embargo, se obtuvo una correlación menor de 0,50 cuando se compararon los valores de [H⁺] medidos con los obtenidos por ambas ecuaciones, Stewart y propuesta (r = 0,491; p<0,001 y r = 0,492; p<0,001, respectivamente).

Los valores de pH y [H⁺] medidos fueron significativamente diferentes de los valores estimados por ambas ecuaciones, Stewart y la propuesta (tabla 2). Sin embargo, no existieron diferencias significativas entre los valores de pH y [H⁺] calculados con ambas ecuaciones (tabla 2), en ninguno de los momentos de medida (reposo, minuto 10, 20 y 30 de la prueba). El promedio de la diferencia de las medias entre los valores de [H⁺] calculados con la ecuación propuesta y con la de Stewart fue de 0,004 ± 0,013 nmol·L^-1, mientras que el promedio de la diferencia de las medias entre los valores de [H⁺] utilizando la ecuación de Stewart y medidos fue de 8,723 ± 6,032 nmol·L^-1, obteniéndose resultados similares (8,727 ± 6,031 nmol·L^-1) al comparar los valores de [H⁺] calculados utilizando la ecuación propuesta y los medidos. En la figura 1 se muestran los gráficos de Bland y Altman para la [H⁺], en los que se pueden observar estos resultados.

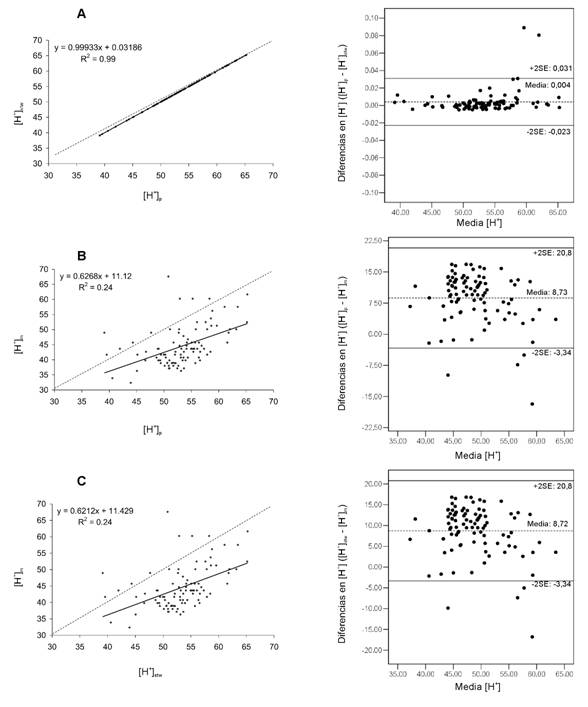
Fig. 1. Los gráficos de la izquierda representan el análisis de regresión lineal (línea continua) y la línea de identidad para la [H⁺]. A) Ecuación de Stewart versus ecuación simplificada propuesta (nmol·L^-1). B) Valores medidos versus ecuación simplificada propuesta (nmol·L^-1). C) Valores medidos versus ecuación de Stewart (nmol·L^-1).

4. DISCUSIÓN

La escasa contribución de los coeficientes D y E en la ecuación de Stewart, permite eliminarlos y trabajar con una ecuación de segundo grado con la que se obtienen resultados similares. Los resultados del presente estudio difieren de los obtenidos por otros autores (4, 6, 18-20). Observamos diferencias significativas entre la [H⁺]medida y estimada por cualquiera de las dos ecuaciones: la ecuación de Stewart y la ecuación simplificada propuesta. Sin embargo, entre la [H⁺]estimada con la ecuación de Stewart y con la ecuación propuesta no hubo diferencias significativas. El procedimiento de Bland y Altman (17) demostró la validez de la nueva ecuación (fig. 1A), verificándose la utilidad de esta en lugar de la ecuación de Stewart de mayor complejidad matemática.

Las diferencias son superiores a 8 nmol.L^-1, al comparar los valores medidos en sangre capilar con los calculados a partir de ambas ecuaciones. Por el contrario, en el trabajo de Kowalchuk y Scheuermann (1994, 1995) las diferencias entre la [H⁺] medida y estimada por la ecuación de Stewart fueron inferiores a 3 nmol.L^-1 (2,1± 7,2 nmol.L^-1), al igual que en el estudio de Heenan y Wolfe (2000), realizado con mujeres gestantes. Estas diferencias, aunque menores que las encontradas en el presente trabajo, también fueron significativas. Además, obtuvieron una alta correlación entre la [H⁺] medida y estimada (r = 0,81) (4), mientras que en el presente estudio la correlación es inferior a 0,50. Otros autores no han obtenido diferencias significativas entre los valores medidos y los calculados a través de la ecuación de Stewart (19, 20), obteniendo una correlación de r = 0,99 (18). Ninguno de estos autores ha utilizado el procedimiento correcto de Bland y Altman para validar la ecuación de Stewart. En el presente trabajo, los gráficos de Bland y Altman demuestran el escaso acuerdo entre los valores medidos y los valores calculados utilizando la ecuación de Stewart (fig. 1C), así como con la ecuación propuesta (fig. 1B). Teniendo en cuenta el escaso acuerdo y la baja correlación obtenida en nuestro estudio (r = 0,49), es posible argumentar que ambas ecuaciones son inadecuadas para determinar la [H⁺], aunque la aproximación de Stewart ofrece un profundo conocimiento del estado ácido-base (22). Las razones que explican por qué la ecuación de Stewart no sirve para determinar la [H⁺] son difíciles de concretar, y podrían estar relacionadas con la imposibilidad de medir todos los iones fuertes o determinar [A_TOT]. Además, la temperatura y la fuerza iónica del plasma pueden influir en los valores de las constantes de equilibrio (ver más adelante).

A partir de una [H⁺] superior a 55 nmol.L^-1 en plasma, las diferencias entre valores medidos y calculados pueden estar sesgados (4), pero en el presente estudio las diferencias se muestran incluso en valores de reposo. En el estudio de Kowalchuk y col. (1988) los valores de [H⁺] medidos y calculados fueron muy parecidos, a excepción de los valores en reposo en sangre arterial, donde hubo una gran variabilidad entre sujetos.

Las razones de las discrepancias entre los resultados de este estudio y los resultados de estudios similares pueden deberse a diversos factores. En primer lugar, aunque diferentes trabajos no han mostrado influencias del tipo de sangre en las medidas ácido-base realizadas (23, 24), nosotros analizamos muestras de sangre capilar, mientras que en el resto de estudios se trabajó con sangre venosa (18), venosa arterializada (4) y sangre arterial (16).

En segundo lugar, no se han medido los ácidos débiles ([A_TOT]), utilizándose para los cálculos el valor medio del estudio de Kowalchuk y Scheuermann (1994, 1995). La concentración total de ácidos débiles ([A_TOT] o [P_TOT]) es la variable independiente que parece tener menor influencia en los resultados, en comparación con la [SID] y la PCO₂ (18). Además, errores en la medida de los ácidos débiles parecen no influir demasiado en la [H⁺] calculada, a valores de [SID] cercanos a 40 mequiv·L^-1 (4, 16).

En tercer lugar, errores al medir las variables independientes que más determinan la [H⁺]: PCO₂, [SID]. Ambas variables determinan los coeficientes de la ecuación de Stewart y de la ecuación propuesta. Sin embargo, los valores obtenidos para estas variables son similares al del resto de estudios. Aunque los coeficientes D y E han sido eliminados en la ecuación propuesta, consideramos que su impacto fisiológico es bajo debido a que la PCO₂ es la única variable independiente incluida en ellos. La metodología utilizada para medir el pH, la PCO₂, los iones fuertes (Na⁺, K⁺, Ca²⁺ y Cl^-) y el lactato fue similar a la utilizada por otros autores (4). Kowalchuk y Scheuermann (1995) señalan que las diferencias pueden deberse a que no todos los iones fuertes son medidos, siendo el valor de [SID] impreciso.

Por último, errores en los valores de las constantes de equilibrio usados para determinar los coeficientes de la ecuación de Stewart. Se han empleado los valores utilizados y recomendados en la literatura, que corresponden a una temperatura de 37º C para el plasma sanguíneo (3, 5, 9, 12). Estas constantes son dependientes de la fuerza iónica y de la temperatura de la solución, y aunque la utilización de valores incorrectos se asocia con pequeños errores, el modelo de Stewart es insensible a errores en la mayoría de las constantes de disociación (4, 5, 16). En el presente estudio se ha asumido el mismo valor de las constantes independientemente de la temperatura central y periférica durante el ejercicio. Aunque el ejercicio se realizó a carga y temperatura constantes, es probable que la temperatura no fuera la misma al comienzo que a la finalización del ejercicio. Sin embargo, el efecto del incremento de la temperatura sobre las constantes para determinar los coeficientes de Stewart es despreciable en un sentido biológico (25). Además, las variaciones en la temperatura no explicarían las diferencias entre la concentración de protones medida y estimada por cualquiera de las dos ecuaciones.

El procedimiento matemático empleado para resolver el polinomio de Stewart no es descrito en ninguno de los trabajos revisados, siendo este aspecto importante a la hora de determinar cuál puede ser la posible causa de las diferencias encontradas entre la [H⁺] medida y estimada, al comparar los resultados de otros estudios y este trabajo.

5. CONCLUSIONES

En conclusión, ni la ecuación de Stewart ni la versión simplificada propuesta, parecen dar una estimación válida de la [H⁺], cuando los resultados se comparan con los obtenidos experimentalmente. De todas formas, la ecuación propuesta puede ser usada para estimar la [H⁺] en lugar de la ecuación de Stewart, ya que los resultados del presente trabajo demuestran su validez y menor complejidad. Futuros trabajos en condiciones de acidosis severa, en las que la [H⁺] es más alta que la estudiada en el presente trabajo, demostrarán si las estimaciones realizadas por la ecuación propuesta se aproximan a los valores medidos.

6. RELEVANCIA FISIOLÓGICA

El análisis fisico-químico del estado ácido-base de los fluidos corporales desarrollado por Stewart es utilizado en diferentes campos.
Resolver la ecuación de Stewart tiene la desventaja de tener que utilizar softwares específicos para resolver una ecuación de cuarto grado.
La contribución de los coeficientes D y E es pequeña en el resultado final y pueden ser eliminados de la ecuación, obteniendo una ecuación de segundo grado más fácil de resolver.
Ninguna de las dos ecuaciones (Stewart y simplificada propuesta) son buenas estimadoras de la [H⁺].

7. REFERENCIAS BIBLIOGRÁFICAS

1. Constable PD. A simplified strong ion model for acid-base equilibria: application to horse plasma. J Appl Physiol. 1997 Jul;83(1):297-311.

2. Heigenhauser GJ. A quantitative approach to acid-base chemistry. Can J Appl Physiol. 1995 Sep;20(3):333-40.

3. Stewart PA. Modern quantitative acid-base chemistry. Can J Physiol Pharmacol. 1983 Dec;61(12):1444-61.

4. Kowalchuk JM, Scheuermann BW. Acid-base regulation: a comparison of quantitative methods. Can J Physiol Pharmacol. 1994 Jul;72(7):818-26.

5. Kowalchuk JM, Scheuermann BW. Acid-base balance: origin of plasma [H+] during exercise. Can J Appl Physiol. 1995 Sep;20(3):341-56.

6. Kowalchuk JM, Heigenhauser GJ, Lindinger MI, Sutton JR, Jones NL. Factors influencing hydrogen ion concentration in muscle after intense exercise. J Appl Physiol. 1988 Nov;65(5):2080-9.

7. Lindinger MI. Origins of [H+] changes in exercising skeletal muscle. Can J Appl Physiol. 1995 Sep;20(3):357-68.

8. Tuhay G, Pein MC, Masevicius FD, Kutscherauer DO, Dubin A. Severe hyperlactatemia with normal base excess: a quantitative analysis using conventional and Stewart approaches. Crit Care. 2008;12(3):R66.

9. Figge J, Rossing TH, Fencl V. The role of serum proteins in acid-base equilibria. J Lab Clin Med. 1991 Jun;117(6):453-67.

10. Kurtz I, Kraut J, Ornekian V, Nguyen MK. Acid-base analysis: a critique of the Stewart and bicarbonate-centered approaches. Am J Physiol Renal Physiol. 2008 May;294(5):F1009-31.

11. Fidkowski C, Helstrom J. Diagnosing metabolic acidosis in the critically ill: bridging the anion gap, Stewart, and base excess methods. Can J Anaesth. 2009 Mar;56(3):247-56.

12. Stewart PA. How to understand acid - base: a quantitative acid - base primer for biology and medicine. New York: Elsevier North Holland; 1981.

13. Peinado PJ, Di Salvo V, Pigozzi F, Bermudez AI, Peinado Lozano AB, Calderon Montero FJ, et al. Steady-state acid-base response at exercise levels close to maximum lactate steady state. Clin J Sport Med. 2006 May;16(3):244-6.

14. Wasserman K, Whipp BJ, Koyl SN, Beaver WL. Anaerobic threshold and respiratory gas exchange during exercise. J Appl Physiol. 1973 Aug;35(2):236-43.

15. Gaskill SE, Ruby BC, Walker AJ, Sanchez OA, Serfass RC, Leon AS. Validity and reliability of combining three methods to determine ventilatory threshold. Med Sci Sports Exerc. 2001 Nov;33(11):1841-8.

16. Fedde MR, Pieschl RL, Jr. Extreme derangements of acid-base balance in exercise: advantages and limitations of the Stewart analysis. Can J Appl Physiol. 1995 Sep;20(3):369-79.

17. Bland JM, Altman DG. Statistical methods for assessing agreement between two methods of clinical measurement. Lancet. 1986 Feb 8;1(8476):307-10.

18. Weinstein Y, Magazanik A, Grodjinovsky A, Inbar O, Dlin RA, Stewart PA. Reexamination of Stewart's quantitative analysis of acid-base status. Med Sci Sports Exerc. 1991 Nov;23(11):1270-5.

19. Preston RJ, Heenan AP, Wolfe LA. Physicochemical analysis of phasic menstrual cycle effects on acid-base balance. Am J Physiol Regul Integr Comp Physiol. 2001 Feb;280(2):R481-7.

20. Kemp JG, Greer FA, Wolfe LA. Acid-base regulation after maximal exercise testing in late gestation. J Appl Physiol. 1997 Aug;83(2):644-51.

21. Heenan AP, Wolfe LA. Plasma acid-base regulation above and below ventilatory threshold in late gestation. J Appl Physiol. 2000 Jan;88(1):149-57.

22. Lindinger MI, Kowalchuk JM, Heigenhauser GJ. Applying physicochemical principles to skeletal muscle acid-base status. Am J Physiol Regul Integr Comp Physiol. 2005 Sep;289(3):R891-4.

23. Forster HV, Dempsey JA, Thomson J, Vidruk E, DoPico GA. Estimation of arterial PO2, PCO2, pH, and lactate from arterialized venous blood. J Appl Physiol. 1972 Jan;32(1):134-7.

24. Linderman J, Fahey TD, Lauten G, Brooker AS, Bird D, Dolinar B, et al. A comparison of blood gases and acid-base measurements in arterial, arterialized venous, and venous blood during short-term maximal exercise. Eur J Appl Physiol Occup Physiol. 1990;61(3-4):294-301.

25. Johnson RLJ, Heigenhauser GJF, Hsia CCW, Jones NL, Wagner PD. Determinants of gas exchange and acid-base balance during exercise. In: Rowell LB, Shepherd JT, editors. Handbook of physiology. New York: Oxford University Press; 1996. p. 515 - 84.

Rev.int.med.cienc.act.fís.deporte- vol. 11 - número 41 - marzo 2011 - ISSN: 1577-0354

Tabla 2. Diferencias entre los valores de pH y [H⁺] medidos y los estimados utilizando la ecuación de Stewart y la ecuación simplificada propuesta. Los datos son mostrados como medias ± DE. pH_m, [H⁺]_m: valores de pH y [H⁺] medidos. pH_stw, [H⁺]_stw: valores estimados de pH y [H⁺] utilizando la ecuación de Stewart. pH_p, [H⁺]_p: valores estimados de pH y [H⁺] usando la ecuación simplificada propuesta. * Diferencias significativas con el pH medido (p<0,05). ^†Diferencias significativas con la [H⁺] medida (p<0,05).
	pH_m	[H⁺]_m (nmol.L^-1)	pH_stw	[H⁺]_stw (nmol.L^-1)	pH_p	[H⁺]_p (nmol.L^-1)
Reposo	7,41±0,02	39,02±1,50	7,30±0,02^*	50,60±2,40^†	7,30±0,02^*	50,60±2,40^†
Min 10	7,32±0,06	48,92±7,44	7,26±0,04^*	55,34±5,15^†	7,26±0,04^*	55,34±5,15^†
Min 20	7,34±0,06	45,77±6,59	7,27±0,05^*	54,05±5,56^†	7,27±0,05^*	54,06±5,56^†
Min 30	7,36±0,05	44,11±4,83	7,28±0,05^*	52,72±5,78^†	7,28±0,05^*	52,72±5,78^†