Rev.int.med.cienc.act.fís.deporte- vol. 11 - número 41 - marzo 2011 - ISSN: 1577-0354

Peinado, A.B., Díaz, V.; Benito, P.J.; Álvarez, M. y Calderón, F.J. (2011). Simplificación de la ecuación de Stewart para valorar el estado ácido-base. Revista Internacional de Medicina y Ciencias de la Actividad Física y el Deporte vol. 10 (41) pp. 115-126. Http://cdeporte.rediris.es/revista/revista41/artecuacion197.htm

Texto en PDF

ORIGINAL

ECUACIÓN SIMPLIFICADA DE STEWART PARA VALORAR EL ESTADO ÁCIDO-BASE EN EJERCICIO

A SIMPLIFICATION OF THE STEWART EQUATION TO DETERMINE ACID-BASE STATUS IN EXERCISE

Peinado, A.B.¹; Díaz, V.²; Benito, P.J.³; Álvarez, M.⁴ y Calderón, F.J.⁵

¹Doctora en Ciencias de la Actividad Física y del Deporte. Profesora Ayudante Doctor, Facultad de Ciencias de la Actividad Física y del Deporte – INEF. Universidad Politécnica de Madrid, España (anabelen.peinado@upm.es).

²Doctor en Ciencias de la Actividad Física y del Deporte. Investigador postdoctoral, Facultad de Ciencias de la Actividad Física y del Deporte – INEF. Universidad Politécnica de Madrid, España (victor.diaz@upm.es). Instituto de Fisiología Veterinaria y Zurich Center for Integrative Human Physiology (ZIHP), Universidad de Zurich, Suiza.

³Doctor en Ciencias de la Actividad Física y del Deporte. Profesor Titular Interino, Facultad de Ciencias de la Actividad Física y del Deporte – INEF. Universidad Politécnica de Madrid, España (pedroj.benito@upm.es).

⁴Licenciada en Ciencias de la Actividad Física y del Deporte. Instituto de Fisiología Veterinaria y Zurich Center for Integrative Human Physiology (ZIHP), Universidad de Zurich, Suiza. (mariaalvarezsanchez@gmail.com).

⁵Doctor en Medicina y Cirugía. Profesor Titular de Universidad, Facultad de Ciencias de la Actividad Física y del Deporte – INEF. Universidad Politécnica de Madrid, España (franciscojavier.calderon@upm.es).

Código UNESCO: 2411 Fisiología Humana

Clasificación del Consejo de Europa: 13. Fisiología del deporte

Recibido 9 de septiembre de 2009

Aceptado 3 de noviembre de 2009

RESUMEN

El objetivo del estudio fue simplificar la ecuación de Stewart y verificar la validez de la ecuación propuesta. Veinticuatro varones realizaron un test a carga constante de 30 minutos en tapiz rodante. Fueron tomadas muestras de sangre capilar en reposo y en los minutos 10, 20 y 30 del test. Los parámetros ácido-base fueron analizados con un analizador de gases en sangre y el lactato por método enzimático. La [H⁺] fue calculada usando la ecuación de Stewart y la ecuación propuesta. La diferencia de medias entre la ecuación propuesta y la de Stewart fue de 0,004 nmol.L^-1 para la [H⁺]. Sin embargo, la diferencia de medias entre las ecuaciones y los valores medidos fue mayor de 8 nmol.L^-1 para la [H⁺] (p<0,001). La ecuación propuesta puede ser usada para estimar la [H⁺] en lugar de la ecuación de Stewart, aunque los valores estimados son significativamente diferentes a los valores medidos.

PALABRAS CLAVE: ion hidrógeno, diferencia de iones fuertes, equilibrio ácido-base, lactato, ejercicio a carga constante.

ABSTRACT

The aim of the present study was to simplify the Stewart equation and to test the validity of the proposed form. Twenty-four men performed a constant load exercise test for 30 min on a treadmill. Capillary blood samples were taken at rest, and again 10, 20 and 30 min into the test. Acid-base variables were measured using a blood-gas analyser and lactate levels were measured enzymatically. The [H⁺] was calculated using the Stewart equation: A[H⁺]⁴+B[H⁺]³+C[H⁺]²+D[H⁺]+E=0, and using a proposed, simplified version of this equation: A[H⁺]²+B[H⁺]+C=0. The difference in the mean [H⁺] results obtained with the two equations was 0.004 nmol·L^-1. However, the difference between the means of the equation-derived results and the measured values was highly significant at >8 nmol·L^-1 (p<0.001). The proposed equation can be used to estimate [H⁺] instead of the full Stewart equation, although the values obtained are significantly different to those actually measured.

KEY WORDS: acid-base equilibrium, constant load, hydrogen ion, lactate, strong ions.

1. INTRODUCTION

The traditional approach of the acid-base balance is most commonly expressed as the Henderson-Hasselbach equation (1). Moreover, it has been explained in quantitative terms by the relationship between the pH of the plasma and the intensity of exercise: as the intensity of exercise increases so too does the plasma acid concentration, and therefore also the hydrogen ion concentration ([H⁺]). At the same time there is a reduction in the bicarbonate concentration ([HCO₃^-]) (2). However, this explanation, although simple to understand, has considerable limitations. Firstly, it does not take into account the variables affecting the acid-base status may have different values in the three compartments affected (the intracellular, erythrocyte and plasma compartments), and secondly, it does not take into account that the relationships between these three compartments - variations in one might lead to changes in the other two.

The independent variables that determine the acid-base balance of biological solutions are the partial pressure of carbon dioxide (PCO₂), the difference in the concentration of strong ions ([SID]) (completely dissociated organic and inorganic ions), and the concentration of partially dissociated weak acids ([A_TOT]) (3-8). The main weak acids involved are proteins (especially albumin and globulin) and phosphates (9). The influence of these variables on [H⁺] can be determined using the Stewart or Fencl equations (4), as well as with the simplified strong ion model derived by Constable (10). These quantitative approaches are used to explain the acid-base behavior of simple and complex solutions and offers a novel insight into the pathophysiology of mixed acid-base disorders (1, 10, 11), being very important from a clinical viewpoint. That proposed by Stewart is a fourth degree polynomic equation: A[H⁺]⁴ + B[H⁺]³ + C[H⁺]² + D[H⁺] + E = 0 (3, 12). Solving this equation, however, has the disadvantage that it requires the use of mathematical programs that are difficult to use and it is possible to eliminate the coefficientes D and E due to their scant contribution to the final result. In addition, the equation should include only those terms that are important in the phenomenology of the procedure (10). The aim of the present work was to simplify this equation and to analyse its validity by comparing the [H⁺] values obtained with the traditional and simplified forms, and then by comparing the values predicted by both with measurements of capillary blood [H⁺] made during a constant load exercise test.

2. MATERIALS AND METHODS

2.1. SUBJECTS

The study subjects were 24 healthy men (age 26.7±4.9 years, height 176.1±6.3 m, body weight 72.8±6.7 kg), all students of Sports and Physical Activity Sciences, and all of whom were familiar with treadmill testing. The subjects were explained the nature of the study and informed consent was obtained from each participant, in accordance with the guidelines of the World Medical Association regarding human investigation as outlined in the Helsinki declaration.

2.2. PROTOCOL

The subjects performed two constant load tests on a treadmill (H/P/Cosmos Pulsar 3P 4.0®; H/P/Cosmos Sports & Medical, Nussdorf-Traunstein, Germany). In the first test, the treadmill was set at a fixed slope of 1% and was accelerated by 0.2 km·h^-1 every 12 s until the subject became exhausted. This test was performed in order to determine the two ventilatory thresholds. The second test involved a stable treadmill rate at the load corresponding to the mid point between these two ventilatory thresholds (i.e., a constant load exercise test) (13-15). The volume and composition of the expired air was determined using a Jaeger Oxycon Pro^® apparatus (Erich Jaeger, Hoechberg, Germany).

2.3. BLOOD SAMPLES AND ANALYSIS

Capillary blood samples were taken from the fingertip during the constant load exercise test at 0, 10, 20 and 30 min; all samples were collected using 100 µl heparinised (heparin electrolyte balanced) capillary tubes. Part of each sample (75 µl of whole blood) was used to determine the values for the variables affecting the acid-base status (pH, PCO₂, HCO₃^-), and to determine the concentrations of electrolytes (Na⁺, K⁺, Ca²⁺ and Cl^-). This was performed using an ABL 77® blood gas analyser (Radiometer, Copenhagen, Denmark). The remainder of each samples (25 µl of whole blood) was used to determine the lactate concentration ([Lac^-]) by an enzymatic method using the YSI 1500® kit (Yellow Springs Instruments Co., Yellow Springs, USA). Both analytical systems were calibrated before each test. The lactate analyser was calibrated using knowed solutions with a [Lac^-] of 5 mmol·L^-1 and 15 mmol·L^-1. The blood gas analyser was calibrated automatically following instructions of the manufacturer.

2.4. CALCULATIONS

The Stewart equation (3, 12) was used to determine [H⁺]:

Equation 1

A[H⁺]⁴ + B[H⁺]³ + C[H⁺]² + D[H⁺] + E = 0

where A = 1, B = K_A + [SID], C = (K_A [SID] - [A_TOT]) - (K_c · PCO₂ + K_w^{`</sup>), D = [K<sub>A</sub> (K<sub>c</sub> · PCO<sub>2</sub> + K<sub>w</sub><sup>`}) + (K₃ · K_C · PCO₂)], and E = K_A · K₃ · K_C · PCO₂. The [SID] was calculated using the values for the electrolytes obtained with the blood gas analyser and using the following formula: [SID] = ([Na⁺]+ [K⁺] + [Ca²⁺]) – ([Cl^-] + [Lac^-]) (4). For [A_TOT], the mean value of 18.2 mequiv·L^-1 reported by other authors (4, 5) was used. K_A (3.0 x 10^-7 ([equiv·L^-1]), K_C (2.46 x 10^-11 [equiv·L^-1]²/Torr), K₃ (6.0 x 10^-11 [equiv·L^-1]), and K´w (4.4 x 10^-14 [equiv·L^-1]²) are the dissociation constants of the weak acids, of carbonic acid, of bicarbonate, and of water respectively. The above values for these constants were those used by other authors (3-6, 12, 16). Matlab v.7.1.0.246 software (MathWorks, Inc. Natick, USA) was used to solve the Stewart equation.

Given the scant contribution of coefficients D and E to the final result, these were eliminated from the equation to give. Then, [H⁺] was calculated using a proposed, simplified version of the Stewart equation. Firstly:

Equation 2

A[H⁺]⁴ + B[H⁺]³ + C[H⁺]² = 0

which was then simplified to:

A[H⁺]² + B[H⁺] + C = 0

2.5. STATISTICAL ANALYSIS

One way ANOVA was used to compare the pH and [H⁺] values measured with the blood gas analyser and those estimated by the Stewart and simplified Stewart equations. When significant differences were detected, a post-hoc Scheffé test was performed. To test the validity of the simplified equation, linear regression analysis was performed, Pearson correlation coefficients were calculated, and, following the method of Bland and Altman (17), graphs were produced to show the differences between the means of the measured pH and [H⁺] values and those calculated using the two forms of the Stewart equation. The determination coefficient (r²) was used to estimate the proportion of the variance explained by the proposed equation. All statistical calculations were undertaken using SPSS v.12.0 software (SPSS Worldwide Headquarters, Chicago, IL) for Windows. Significance was set at α < 0.05.

3. RESULTS

The mean values measured for pH and [H⁺] were significantly different to those calculated by the traditional and simplified Stewart equations. However, no significant differences were seen between both equations.

Table 1 shows the means ± SD for the [SID], PCO₂ and [Lac^-] measures obtained by the blood gas and the lactate analyser (see above).

Table 1. Descriptive data. Data are shown as means ± SD for the [SID], PCO2 and [Lac^-].
	[SID] (mequiv.L^-1)	[Lac^-] (mmol.L^-1)	PCO2 (mmHg)
At rest	39.1 ± 12.15	1.52 ± 0.53	36.21 ± 3.50
Min 10	32.64 ± 3.58	4.87 ± 2.09	35.79 ± 3.54
Min 20	33.5 ± 3.93	4.85 ± 1.97	31.88 ± 2.71
Min 30	34.42 ± 4.20	4.31 ± 2.08	30.92 ± 3.68

Table 2 shows the means ± SD for the pH and [H⁺] determined by measurement, by the traditional Stewart equation, and by the proposed, simplified Stewart equation (Equations 1 and simplified equation 2 respectively).

Table 2. Differences between the measured pH and [H^+] values, those estimated using the Stewart equation and the proposed, simplified Stewart equation. Data are shown as means ± SD. pHm, [H^+]m: Measured pH and [H^+] values. pHstw, [H^+]stw: Estimated values using the Stewart equation. pHp, [H^+]p: Estimated values using the proposed, simplified Stewart equation. * Significantly different to measured pH (p<0.05). ^†Significantly different to measured [H^+] (p<0.05).
	pHm	[H^+]m (nmol.L^-1)	pHstw	[H^+]stw (nmol.L^-1)	pHp	[H^+]p (nmol.L^-1)
At rest	7.41±0.02	39.02±1.50	7.30±0.02^*	50.60±2.40^†	7.30±0.02^*	50.60±2.40^†
Min 10	7.32±0.06	48.92±7.44	7.26±0.04^*	55.34±5.15^†	7.26±0.04^*	55.34±5.15^†
Min 20	7.34±0.06	45.77±6.59	7.27±0.05^*	54.05±5.56^†	7.27±0.05^*	54.06±5.56^†
Min 30	7.36±0.05	44.11±4.83	7.28±0.05^*	52.72±5.78^†	7.28±0.05^*	52.72±5.78^†

Figure 1 shows the dispersion diagrams. A high correlation was obtained between the [H⁺] values calculated by the traditional and simplified Stewart equations (r = 0.999; p<0.001); however the correlation coefficients between the measured [H⁺] values and those determined by the two forms of the Stewart equation were both <0.50 (r = 0.491; p<0.001, and r = 0.492; p<0.001), respectively).

The mean measured pH and [H⁺] values were significantly different to those calculated by either Stewart equations (Table 2). However, no significant differences were seen between the pH and [H⁺] values calculated with either of the Stewart equations at any particular time point (0, 10, 20 or 30 min) (Table 2). The average difference between the mean [H⁺] values determined by the traditional and proposed Stewart equations was 0.004 ± 0.013 nmol.L^-1, while that between the mean measured [H⁺] values and the traditional Stewart equation-determined results was 8.723 ± 6.032 nmol.L^-1. Similar differences were obtained in comparisons between the mean measured and the proposed Stewart equation-determined results (8.727 ± 6.031 nmol.L^-1). Figure 1 shows the Bland and Altman graphs for [H⁺], in which these comparisons can be seen.

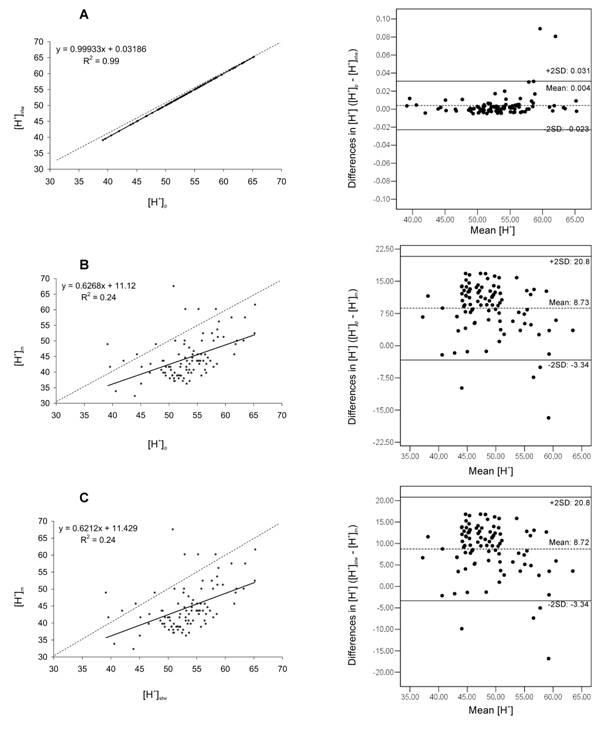
Fig. 1. The graphs at the left represent the linear regression analysis (continuous line) and the line of complete similarity (dotted line) for [H⁺]. A) Stewart ecuation vs. proposed, simplified Stewart equation (nmol·L^-1). B) Measured values vs. proposed, simplified Stewart equation (nmol·L^-1). C) Measured values vs. traditional Stewart equation (nmol·L^-1).

4. DISCUSSION

We have found a little contribution of coefficients D and E of the Stewart´s equation, which allow the possibility to work with a second degree equation obtaining similar results. The results of the present work differ to those obtained by other authors (4, 6, 18-20). Significant differences were seen between the measured and Stewart equation-estimated (either form) [H⁺]. However, no significant differences were seen between the [H⁺] determined by the traditional and proposed Stewart equations. The Bland and Altman procedure (17) confirmed the validity of the proposed equation (Fig. 1A), which can therefore be used in place of the mathematically more complex traditional Stewart equation.

The differences between the mean [H⁺] values measured in the capillary blood and those determined using either equation were >8 nmol·L^-1; this contrasts with the results obtained by Kowalchuk and Scheuermann (1994, 1995) who reported the difference in the mean measured and traditional Stewart equation-derived [H⁺] values to be <3 nmol·L^-1 (2.1± 7.2 nmol.L^-1). Heenan y Wolfe (2000) reported similarly small differences in their study of pregnant women. However, the differences detected by these other authors were also significant. In addition, (4) found a strong correlation between the mean measured and estimated [H⁺] values (r =0.81), while in the present work the correlation coefficient was r <0.50. Other authors report significant differences between mean measured [H⁺] values and those calculated using the traditional Stewart equation (19, 20), along with a correlation coefficient of r = 0.99 (18). However, none of these authors used Bland and Altman graphs to validate the Stewart equation. In the present work, these graphs showed a poor agreement between the measured [H⁺] values and those determined by the traditional (Fig. 1C) and proposed, simplified (Fig. 1B) equations. Taking in accuount the poor agreement and low correlation in our study (r = 0.49) is possible to argue that both equations are inappropriate to determine the [H⁺], but the Stewart´s approach offers a deeper knowledge of the acid-base status (22). The reasons to explain why Stewart´s equation could fail when determinig the pH are difficult to explain and could be related with the impossibilty to measure all the strong ions or determine A_TOT. Also, the temperature and ionic strength of the plasma are influencing the values of the equilibrium constants (see also below).

When the plasma [H⁺] is >55 nmol·L^-1, the differences between the measured and calculated values have been reported to increase (4), but in the present study the difference remained the same throughout. In the study of Kowalchuk et al. (1988) calculated and measured [H⁺] were closely comparable, apart from arterial plasma at rest, where there was a marked variability between the subjects.

The reasons for the differences between the results of this study and those of other authors could be due to several factors. Although several works have shown no differences in acid-base measurements depending on the type of blood (23, 24), we used capillary blood while Weinstein et al. (1991) used venous blood, Kowalchuk and Scheuermann (1994) used arterialised venous blood, and Fedde and Pieschl (1995) used arterial blood. Secondly, [A_TOT] was not measured in the present work; rather, the mean value reported by (4, 5) was used; [A_TOT] (or [P_TOT]) appears to influence the results much less than [SID] or PCO₂ (18). In addition, errors in the measurement of [A_TOT] do not appear to influence the calculated [H⁺] values when the [SID] is close to 40 mequiv·L^-1 (4, 16). Finally, errors in the measurement of the independent variables with most influence on [H⁺] - PCO₂ and [SID] – may explain some of these differences. Both variables determine the coefficients of the traditional and proposed Stewart equations. The values obtained for these variables were similar to those obtained in all other studies. Although the coefficients D and E have been eliminated in the propoesed equation, we consider that the physiological impact of deleting them is low because PCO₂ is the only independient variable included in them.

The methodology used to measure the pH, PCO₂, and the strong ion (Na⁺, K⁺, Ca⁺² and Cl^-) and lactate concentrations was similar to that employed by (4). Kowalchuk and Scheuermann (1995) reported that differences between the measured and calculated [H⁺] values in their study might be due to the fact not all the strong ions are measured, leading to an inaccurate [SID]. Finally, errors in the values of the equilibrium constants used to determine the coefficients of the Stewart equation may explain some of these differences. In the present study, values recommended in the literature were used, which correspond to a blood plasma temperature of 37ºC (3, 5, 9, 12). These constants, however, are dependent on the temperature and ionic strength of the plasma. Nonetheless, the use of incorrect values is only associated with small errors since the Stewart equation is largely insensitive to inaccuracies in the majority of the dissociation constants (4, 5, 16). In the present work, the same values were assumed for the equilibrium constants independent of the difference between the central and peripheral temperatures during exercise. In addition, although the constant load exercise was assumed to have been performed at a constant body temperature, it is likely that it was not the same at the beginning and the end of the exercise. However, the effect of increasing temperature on the factors required to determine the Stewart equation constants is negligible from a biological point of view (25). Further, temperature variation cannot explain the differences between the mean measured and Stewart equation-derived (either form) [H⁺] values.

None of the studies mentioned above discuss the mathematical procedure used to solve the polynomial Stewart equation, yet this is important when trying to determine the possible causes of differences in the measured and estimated [H⁺] values.

5. CONCLUSIONS

In conclusion, neither the Stewart equation nor the proposed simplified version appear to provide a particularly valid estimate of [H⁺] when compared to experimentally obtained results. However, the simplified equation can be employed in lieu of the full equation since it provides the same results yet is easier to use. Future work should examine the estimates provided by the proposed equation in conditions of severe acidosis, in which the [H⁺] is higher than that studied in the present work.

6. PHYSIOLOGICAL RELEVANCE

• The physicochemical analysis of body fluid acid-base status developed by Stewart is used in a several fields.
• To solve the Stewart´s equation has the disadvantage to work with a four degree equation and specific software.
• The contribution of coefficients D and E is little to the final result and can be eliminated from the equation, obtaining a second dregree equation easier to solve.
• Neither Stewart´s equation nor proposed equation in this work are able to make a good estimation of [H⁺].

7. REFERENCES

1. Constable PD. A simplified strong ion model for acid-base equilibria: application to horse plasma. J Appl Physiol. 1997 Jul;83(1):297-311.

2. Heigenhauser GJ. A quantitative approach to acid-base chemistry. Can J Appl Physiol. 1995 Sep;20(3):333-40.

3. Stewart PA. Modern quantitative acid-base chemistry. Can J Physiol Pharmacol. 1983 Dec;61(12):1444-61.

4. Kowalchuk JM, Scheuermann BW. Acid-base regulation: a comparison of quantitative methods. Can J Physiol Pharmacol. 1994 Jul;72(7):818-26.

5. Kowalchuk JM, Scheuermann BW. Acid-base balance: origin of plasma [H+] during exercise. Can J Appl Physiol. 1995 Sep;20(3):341-56.

6. Kowalchuk JM, Heigenhauser GJ, Lindinger MI, Sutton JR, Jones NL. Factors influencing hydrogen ion concentration in muscle after intense exercise. J Appl Physiol. 1988 Nov;65(5):2080-9.

7. Lindinger MI. Origins of [H+] changes in exercising skeletal muscle. Can J Appl Physiol. 1995 Sep;20(3):357-68.

8. Tuhay G, Pein MC, Masevicius FD, Kutscherauer DO, Dubin A. Severe hyperlactatemia with normal base excess: a quantitative analysis using conventional and Stewart approaches. Crit Care. 2008;12(3):R66.

9. Figge J, Rossing TH, Fencl V. The role of serum proteins in acid-base equilibria. J Lab Clin Med. 1991 Jun;117(6):453-67.

10. Kurtz I, Kraut J, Ornekian V, Nguyen MK. Acid-base analysis: a critique of the Stewart and bicarbonate-centered approaches. Am J Physiol Renal Physiol. 2008 May;294(5):F1009-31.

11. Fidkowski C, Helstrom J. Diagnosing metabolic acidosis in the critically ill: bridging the anion gap, Stewart, and base excess methods. Can J Anaesth. 2009 Mar;56(3):247-56.

12. Stewart PA. How to understand acid - base: a quantitative acid - base primer for biology and medicine. New York: Elsevier North Holland; 1981.

13. Peinado PJ, Di Salvo V, Pigozzi F, Bermudez AI, Peinado Lozano AB, Calderon Montero FJ, et al. Steady-state acid-base response at exercise levels close to maximum lactate steady state. Clin J Sport Med. 2006 May;16(3):244-6.

14. Wasserman K, Whipp BJ, Koyl SN, Beaver WL. Anaerobic threshold and respiratory gas exchange during exercise. J Appl Physiol. 1973 Aug;35(2):236-43.

15. Gaskill SE, Ruby BC, Walker AJ, Sanchez OA, Serfass RC, Leon AS. Validity and reliability of combining three methods to determine ventilatory threshold. Med Sci Sports Exerc. 2001 Nov;33(11):1841-8.

16. Fedde MR, Pieschl RL, Jr. Extreme derangements of acid-base balance in exercise: advantages and limitations of the Stewart analysis. Can J Appl Physiol. 1995 Sep;20(3):369-79.

17. Bland JM, Altman DG. Statistical methods for assessing agreement between two methods of clinical measurement. Lancet. 1986 Feb 8;1(8476):307-10.

18. Weinstein Y, Magazanik A, Grodjinovsky A, Inbar O, Dlin RA, Stewart PA. Reexamination of Stewart's quantitative analysis of acid-base status. Med Sci Sports Exerc. 1991 Nov;23(11):1270-5.

19. Preston RJ, Heenan AP, Wolfe LA. Physicochemical analysis of phasic menstrual cycle effects on acid-base balance. Am J Physiol Regul Integr Comp Physiol. 2001 Feb;280(2):R481-7.

20. Kemp JG, Greer FA, Wolfe LA. Acid-base regulation after maximal exercise testing in late gestation. J Appl Physiol. 1997 Aug;83(2):644-51.

21. Heenan AP, Wolfe LA. Plasma acid-base regulation above and below ventilatory threshold in late gestation. J Appl Physiol. 2000 Jan;88(1):149-57.

22. Lindinger MI, Kowalchuk JM, Heigenhauser GJ. Applying physicochemical principles to skeletal muscle acid-base status. Am J Physiol Regul Integr Comp Physiol. 2005 Sep;289(3):R891-4.

23. Forster HV, Dempsey JA, Thomson J, Vidruk E, DoPico GA. Estimation of arterial PO2, PCO2, pH, and lactate from arterialized venous blood. J Appl Physiol. 1972 Jan;32(1):134-7.

24. Linderman J, Fahey TD, Lauten G, Brooker AS, Bird D, Dolinar B, et al. A comparison of blood gases and acid-base measurements in arterial, arterialized venous, and venous blood during short-term maximal exercise. Eur J Appl Physiol Occup Physiol. 1990;61(3-4):294-301.

25. Johnson RLJ, Heigenhauser GJF, Hsia CCW, Jones NL, Wagner PD. Determinants of gas exchange and acid-base balance during exercise. Handbook of physiology Section 12 Exercise: regulation and integration of multiple systems; 1996.

Rev.int.med.cienc.act.fís.deporte- vol. 11 - número 41 - marzo 2011 - ISSN: 1577-0354