Gutiérrez-Dávila, M.; González, C.; Giles, F.J.; Gallardo, D. y Rojas, F.J. (2016). Efecto de sobrecargas ligeras sobre el rendimiento del salto vertical con contramovimiento / Effect Of Light Overloads On Countermovement Vertical Jump Performance. Revista Internacional de Medicina y Ciencias de la Actividad Física y el Deporte vol. 16 (64) pp. 633-648 Http://cdeporte.rediris.es/revista/revista64/artefecto770.htm

DOI: http://dx.doi.org/10.15366/rimcafd2016.64.002

Texto en PDF

English version PDF

ORIGINAL

EFECTO DE SOBRECARGAS LIGERAS SOBRE EL RENDIMIENTO DEL SALTO VERTICAL CON CONTRAMOVIMIENTO

EFFECT OF LIGHT OVERLOADS ON COUNTERMOVEMENT VERTICAL JUMP PERFORMANCE

Gutiérrez-Dávila, M.¹; González, C.²; Giles, F.J.²; Gallardo, D.² y Rojas, F.J.¹

¹ Departamento de Educación Física y Deportiva. Universidad de Granada (España). Profesores de Biomecánica del Movimiento Humano marcosgd@ugr.es, fjrojas@ugr.es

² Estudiantes de Grado en Ciencias de la Actividad Física y el Deporte

carmen13@correo.ugr.es, jgiles@correo.ugr.es, diegogallardo@correo.ugr.es

Código UNESCO / UNESCO code: 2406.04 Biomecánica / Biomechanics.

Clasificación del Consejo de Europa / Council of Europe classification: 3. Biomecánica del deporte / Biomechanics of sport

Recibido 27 de febrero de 2014 Received February 27, 2014

Aceptado 24 de mayo de 2014 Accepted May 24, 2014

RESUMEN

El propósito de este estudio ha sido determinar el efecto de diferentes sobrecargas ligeras sobre el impulso vertical, la velocidad del centro de masas y el máximo pico de potencia, durante la realización de dos saltos verticales máximos consecutivos. Han participado 28 deportistas practicantes de modalidades deportivas donde el salto vertical constituye una habilidad básica. Se ha utilizado una plataforma de fuerza, operando a 500 Hz, sincronizada temporalmente a una cámara de vídeo, que registraba a 210 Hz el plano sagital de los saltos realizados sobre la plataforma. Los resultados indican que, cuando se utilizan sobrecargas del 7,5% del peso corporal, el tiempo utilizado durante la fase de contramovimiento se incrementa. El impulso vertical y el pico de potencia no varían con el uso de los diferentes niveles de las sobrecargas utilizadas, sin embargo, la velocidad de despegue se reduce un porcentaje similar al incremento de la carga.

PALABRAS CLAVE: Biomecánica, fuerza, impulso, sobrepeso, salto vertical.

ABSTRACT

The purpose of this study was to determine the effect of different light overloads on the vertical impulse, velocity of center of mass and peak power during two consecutive maximum vertical jumps. 28 athletes practicing different sports where vertical jump is a basic skill have participated. A force platform, operating at 500 Hz, temporally synchronized to a video camera, which recorded at 210 Hz the sagittal plane of the jumps were used for the analysis. The results have shown that when overloads of 7,5% of body weight were used , the time used for the counter- phase increased. The vertical impulse and peak power did not vary with the use of different levels of light overloads used in this study, however, the take-off velocity the CM was reduced with a similar percentage that increased the overload.

KEYWORDS: Biomechanics, force, impulse, overweight, vertical jump.

INTRODUCCIÓN

Desde una perspectiva biomecánica, en los movimientos explosivos complejos, la coordinación de los impulsos parciales que producen los diferentes grupos musculares, constituye uno de los factores de eficacia más relevantes. Además, es necesario considerar que, tanto la fuerza muscular como su velocidad de contracción, son dependientes de la masa y la inercia contra la que actúa dicha fuerza. Partiendo de esta teorización biomecánica, al incrementar la masa, se reduciría la velocidad de acortamiento muscular y, consecuentemente, se modificaría el rendimiento dinámico de la contracción muscular.

Por ejemplo, es conocido que, cuando la actividad muscular se orienta hacia la manipulación de cargas pesadas, la fuerza estática máxima tiende a incrementarse, mientras que la máxima velocidad de contracción muscular permanece inalterada o incluso puede disminuir. Como resultado, además de incrementarse la potencia muscular, existe un desplazamiento del pico de potencia máximo (PP) para adaptarse a las cargas más pesadas. (Fitts y Widick, 1996; Shoepe, y cols. 2003). Por el contrario, cuando se manipulan cargas más ligeras, también aumenta la fuerza muscular, pero el PP no se desplaza (Kaneko y cols., 1983). Concretamente, para los saltos verticales, las investigaciones precedentes parecen confirmar una hipótesis general donde la carga óptima para obtener la máxima producción de energía y el pico máximo de potencia, en persona habitualmente activas, se produce acelerando el propio cuerpo (Dugan y cols., 2004; Cormie y cols., 2007a; Markovic y Jaric, 2007; Cormie, y cols., 2008; Jaric y Markovic, 2009; McBride, y cols., 2010). Aunque la hipótesis expuesta parece estar suficientemente contrastada, al analizar las diversas metodologías, los tipos de saltos y las muestras utilizadas en esas investigaciones, es necesario ser cautos con los resultados que las avalan.

Generalmente, cuando se informa que la carga óptima para obtener la máxima producción de energía y pico de potencia en los saltos verticales es la propia masa corporal, no se ha tenido en cuenta que los pies y las piernas representan el 12 % de la masa corporal y éstos permanecen estáticos durante gran parte del salto vertical. Así, ciertas investigaciones han sugerido un ajuste en la masa, considerando sólo la masa que se desplaza (Cormie y cols., 2007b). Por otra parte, durante los saltos verticales, la masa de los segmentos superiores está sujeta a ciertas aceleraciones. Como consecuencia, producen una fuerza adicional que modifica la carga externa (fuerza inercial). Por ejemplo, en los saltos verticales realizados con participación segmentaria (acción de brazos), se incrementan la fuerza neta vertical, el tiempo de aplicación de fuerza y la velocidad de despegue del centro de masas (CM) (Aragón-Vargas, 2000; Feltner, y cols., 1999; Hara y cols., 2006; Lees y cols., 2004; Gutiérrez-Dávila y cols., 2012). Para evitar este inconveniente, la mayoría de las investigaciones que avalan la hipótesis expuesta, han utilizado protocolos donde se restringen las aceleraciones de los segmentos superiores durante el salto, lo que constituye una limitación que nos aleja de la realidad.

En relación a las muestras utilizadas, se ha comprobado que la carga que proporciona el máximo PP es diferente en deportistas entrenados, con respecto a los no entrenados (Driss y cols., 2001; Stone y cols., 2003). Esta evidencia nos permite considerar que el entrenamiento puede variar ciertas propiedades mecánicas de los músculos que están estrechamente relacionadas con el rendimiento dinámico. En este sentido, Driss y cols., (2001), utilizando el protocolo saltos partiendo desde cuclillas con restricción segmentaria (Squat Jump), han confirmado que el máximo PP se consigue acelerando su propia masa en personas sedentarias, mientras que, cuando se trata de deportistas entrenados en fuerza y potencia, las cargas ligeras (entre 5-10 Kg), no tienen efecto sobre el PP.

El uso de las sobrecargas ligeras en el ámbito del entrenamiento deportivo ha estado asociado a la utilización de cinturones y chalecos lastrados. En unas ocasiones incorporado como carga adicional, con el propósito de estudiar sus efectos en las actividades que implican desplazamientos rápidos (Cronin y cols., 2008; Clark y cols., 2010) y, en otras ocasiones, para determinar su efecto sobre la capacidad de salto (Faigenbaum, y cols., 2006; Thompsem, y cols., 2007; Khlifa y cols., 2010). Sin embargo, aunque estos dispositivos no restringen el movimiento, son escasos los datos que confirman su efecto en situaciones de salto vertical con contramovimiento y participación segmentaria libre, es decir, utilizando protocolos próximos a las situaciones reales de competición.

Según lo expuesto, el propósito de este estudio ha sido determinar el efecto que tiene el uso de chalecos lastrados con diferentes sobrecargas ligeras (2,5; 5 y 7,5 % de la masa corporal) sobre el impulso, la velocidad del CM y el máximo pico de potencia, durante la realización de dos saltos verticales máximos consecutivos sin restricción segmentaria, considerado como uno de los protocolos de salto vertical más apropiados para el análisis de actividades pliométricas que implican el ciclo estiramiento-acortamiento (Wallace y cols. 2010).

MÉTODO

Participantes

Han participado 26 estudiantes de la Facultad de Ciencias de la Actividad Física y del Deporte (edad = 21,4 ± 2,1 años; talla = 1,79 ± 0,05 m; masa = 71,2 ± 6,9 Kg; IMC = 22,3 ± 1,8 Kgm^-2 ), utilizando para su selección el criterio de haber participado de forma regular en actividades deportivas donde el salto vertical constituye una habilidad básica (voleibol, baloncesto, balonmano, fútbol y atletismo). A todos los participantes se les informó y solicitó su consentimiento para participar en este estudio siguiendo las directrices de la Comisión Ética de la Universidad de Granada (España).

Materiales y procedimientos

Se ha utilizado una plataforma de fuerza de 0,6 x 0,37 m, Dinascan/IBV, operando a 500 Hz, sincronizada temporalmente a una cámara de vídeo Casio EX - FH20, que registraba a 210 Hz el plano sagital de los saltos realizados sobre la plataforma. Después de un calentamiento normalizado de quince minutos, los participantes debían realizar dos saltos verticales máximos consecutivos (Figura 1) partiendo de una posición erguida sobre la plataforma e implementados con un chaleco lastrado con una sobrecarga variable con respecto a su masa (0%; 2,5%; 5% y 7,5% de la masa corporal). Antes de comenzar las sesiones de registro, se realizó un proceso de aprendizaje del modelo de salto, así como de adaptación a los sistemas de registro. Siguiendo a Schmidt y Lee (2011), este proceso de aprendizaje finalizó cuando se alcanzaba una estabilidad en los tiempo de batida del segundo salto. Se realizó una sesión de cinco ensayos válidos para cada condición de carga, con una recuperación de 2 minutos entre ensayo y de 10 minutos entre sesión. Se desecharon los ensayos que registraron el mayor y el menor tiempo de vuelo en primer salto y, entre los tres restantes, sólo se analizó el registro mediano del tiempo de vuelo del segundo salto. El orden de las condiciones propuestas para cada sesión fue alterado entre los sujetos.

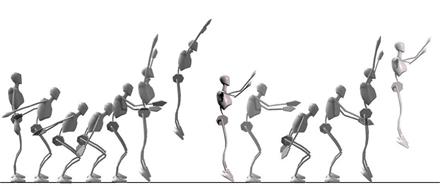
Figura 1. Representación gráfica del modelo utilizado para realizar los dos saltos verticales máximos consecutivos.

Cálculo de las variables biomecánicas

Para cada ensayo, se determinó el posible error sistemático procedente de la plataforma de fuerzas a parir de la media de la fuerza vertical (F_Y) de 20 registros sucesivos tras el despegue del primer salto. Después de restar el posible error sistemático y el peso del sujeto, en cada situación experimental (m_(0); m_(2.5); m₍₅₎ y m_(7.5), respectivamente), se determinó la aceleración vertical del CM, a partir de F_Y y la masa del saltador para cada situación. Finalmente, los sucesivos registros de la velocidad vertical y las posiciones de componente vertical adoptadas por el CM (v_(Y)CM y Y_CM, respectivamente), se determinaron mediante integración de las componentes verticales de las funciones de aceleración-tiempo y velocidad-tiempo, respectivamente, usando para ello el método trapezoidal con un incremento temporal de 0,002 s. Como constante de integración para el primer salto se utilizó la altura del CM en la posición inicial de cada participante y velocidad cero. Para el segundo salto se utilizó la altura y velocidad vertical del CM en el instante de tomar contacto con la plataforma.

El cálculo de las constantes de integración se realizó a partir de las imágenes de vídeo (2D). Para ello, antes de comenzar el registro de los saltos, se filmó un sistema de referencia consistente en un cubo de 2 x 2 x 0.5 m que permitió la conversión de las coordenadas digitalizadas en datos reales. Para determinar la posición inicial del CM del primer salto, se digitalizó manualmente una imagen antes de iniciarse el movimiento, utilizando para ello el modelo y parámetros inerciales propuestos por Zatsiorsky y Seluyanov (1983) y adaptados por De Leva, (1996). Para determinar la posición del CM en la toma de contacto del segundo salto, se digitalizaron doce imágenes consecutivas durante del inicio del segundo salto, donde la sexta imagen correspondía a la toma de contacto con la plataforma. Así, el contacto se produce durante el intervalo comprendido entre la 5ª y 6ª imagen (un intervalo de 0.0047 s). Las coordenadas planas de las doce imágenes fueron suavizadas mediante un filtro digital de paso bajo, a 8 Hz (Winter, 1990). Las posiciones del CM para cada imagen se determinaron utilizando el mismo modelo y parámetros inerciales utilizados para el primer salto. Finalmente, la posición inicial del CM para el segundo fue el valor medio de las posiciones del CM correspondientes a la 5ª y 6ª imagen. La velocidad vertical instantánea del CM se determinó mediante la primera derivada de la posición vertical del CM, con respecto al tiempo (mitad del intervalo ente la 5ª y 6ª imagen), utilizando para ello las funciones quintic splines con suavizado cero (Wood y Jennings, 1979).

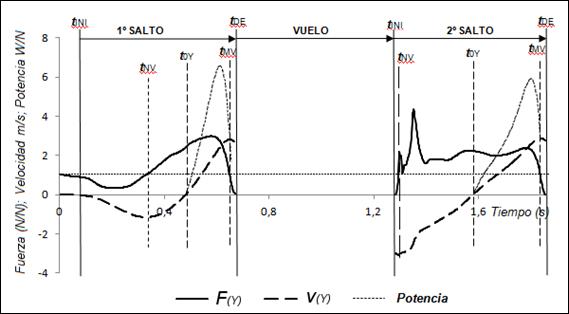
El análisis temporal de los dos saltos se ha dividido en tres fases, siguiendo la metodología propuesta por Feltner y cols., (2004): a) Contramovimiento, que comprende desde el inicio del movimiento hasta que la velocidad vertical del CM adquiere un su valor más próximo a cero (t_0Y); b) Propulsión (t_{.(PROPULSIÓN)}), que comprende un periodo temporal entre t_0Y y el instante en que la velocidad vertical del CM alcanza su máximo valor (t_MV) y c): Previa al despegue (t._{(PREVIO-DESPEGUE)}), comprendida entre t_MV y el instante de despegue (t_DE)). En la Figura 2 se representan las citadas fases, junto a la fuerza vertical normalizada con respecto al peso corporal (F_(Y)), la componente vertical de la velocidad del CM (v_(Y)) y la potencia normalizada durante la fase de propulsión, con respecto al tiempo, para uno de los sujetos analizados. Para un análisis detallado del primer salto, la fase de contramovimiento se ha dividido en dos periodos temporales: a₁: Periodo de contramovimiento inicial, que comprende desde el inicio del movimiento hasta el instante donde la velocidad vertical del CM alcanza su máximo valor negativo (t_NV) y a₂: Periodo de contramovimiento final, (t._{(CONTRAM.-FINAL)}) que comprende desde t_NV hasta t_0Y. Debido a las dificultades para localizar el instante donde se produce el inicio del movimiento, no se ha considerado el periodo de contramovimiento inicial.

Figura 2. Representación gráfica de las fases en que se ha dividido el salto vertical a partir de la fuerza vertical normalizada con respecto al peso corporal (F_(Y) y la componente vertical de la velocidad del CM (v_(Y)). En la figura también se representa la potencia normalizada desarrollada durante las fases propulsiva.

El impulso vertical para la fase de contramovimiento del segundo salto y las fases propulsivas más las previas al despegue, para los dos saltos (Iv_(CONTRAM) y Iv_{(PROP.+PREVIO-DESP.)}, respectivamente), se han determinado mediante integración de la función F_(Y) con respecto al tiempo que duran las respectivas fases, usando para ello el método trapezoidal con un incremento temporal de 0,002 s. El pico máximo de potencia durante la fase de propulsión (PP_{(PROPULSIÓN)}) se ha considerado como el máximo valor del producto de la fuerza neta y la velocidad vertical durante la fase de propulsión. El tiempo en que se produce el pico máximo de potencia (t_{(PP-PROPULSIÓN)}) se ha expresado en porcentaje del tiempo que dura la fase de propulsiva.

Análisis estadístico

Tras comprobar la distribución normal de los datos y para evaluar la fiabilidad de las pruebas, se ha aplicado un análisis de varianza de medidas repetidas a todos los ensayos en las cuatro condiciones experimentales (cinco ensayos para cada condición), tomando como variable dependiente el tiempo de batida del segundo salto (t._(CONTRAM.))+t._{(PROPULSIÓN)}). No existiendo diferencias significativas entre los ensayos. El coeficiente de correlación intraclase para esta misma variable, ha sido de 0,984 (p< 0,001) para la condición sin carga adicional (0%), de 0,987 (p< 0,001) para el 2,5% (p< 0,001) de 0,988 (p< 0,001) para 5% y de 0,982 (p< 0,001) para 7,5%.

Se ha calculado la media y desviación típica para cada variable en cada situación experimental, determinándose las diferencias entre las medias de los cuatro niveles de la variable (0%; 2,5%; 5% y 7,5% de la masa corporal), mediante un análisis de varianza de medidas repetidas (ANOVA). Un análisis múltiple de contrastes posterior determinó entre qué grupos se encontraban las diferencias estadísticamente significativas. El nivel de significación se ha establecido en p<0,05. Se ha utilizado el paquete estadístico Statgraphic Plus 5.1.y SPSS v. 20.0.

RESULTADOS

En la tabla 1 se presentan los datos numéricos de los factores más significativos que determinan la eficacia del primer alto vertical. El tiempo de contramovimiento final (t._{(CONTRAM.-FINAL)}) ha sido significativamente mayor cuando se utiliza una sobrecarga de 7,5 % de la masa (p<0,05) con respecto a cargas más reducida (0%, 2,5% y 5% de la masa), mientras que no han existido diferencias estadísticamente significativas entre las medias, cuando se comparan por pares las sobrecargas inferiores a 7,5% de la masa. Resultados similares se han obtenido para el tiempo de la fase previa al despegue, donde t._{(PREVIO-DESPEGUE)}, ha sido significativamente superior cuando se utiliza una carga del 7,5% de la masa (p<0,01), con respecto al uso de cargas inferiores. La velocidad vertical del CM en el despegue ha disminuido a medida que se incrementaba la carga (p<0,001).

La prueba de contrastes aplicada a esta variable confirma este hecho, existiendo diferencias estadísticamente significativas entre las medias cuando se cruzan por pares las cuatro condiciones experimentales. Aunque no han existido diferencias estadísticamente significativas entre las medias para el pico máximo de potencia durante la fase propulsiva (PP_{(PROPULSIÓN)}), los valores de tendencia central tiende a reducirse a medida que se incrementa la carga. No han existido diferencias entre las medias para el resto de las variables analizadas.

Tabla 1.- Estadística descriptiva y análisis de varianza multifactorial (ANOVA de medidas repetidas), para las variables biomecánicas en las cuatro condiciones de caga (0% 2,5%, 5% y 7,5% con respecto a la masa de cada participante) para el primer salto.

Variables	0% masa^1	2,5% masa^2	5% masa^3	7,5 masa^4	F
t.(CONTRAM.-FINAL) (s)	0,163 ± 0,033	0,166 ± 0,031	0,167 ± 0,029	0,185^1,2,3 ± 0,041	3,94*
t.(PROPULSIÓN) (s)	0,248 ± 0,050	0,257 ± 0,052	0,256 ± 0,042	0,259 ± 0,040	1,20
t.(PREVIO-DESPEGUE) (s)	0,024 ± 0,004	0,024 ± 0,003	0,024 ± 0,004	0,027^1,2,3 ± 0,005	5,29**
v(Y)CM en tNV (ms^-1)	-1,131 ± 0,177	-1,108 ± 0,182	-1,114 ± 0,175	-1,074 ± 0,196	0,86
YCM despegue (m)	1,234 ± 0,064	1,227 ± 0,079	1,236 ± 0,066	1,226 ± 0,060	0,46
v(Y)CM despegue(ms^-1)	2,758 ± 0,183	2,698 ± 0,189^1	2,653 ± 0,202^1,2	2,568^1,2,3 ± 0,196	23,18***
Iv(PROP.+PREVIO-DESP.) (Ns)	196,5 ± 23,8	197,4 ± 26,6	198,6 ± 25,9	196,9 ± 25,5	0,47
PP(PROPULSIÓN) (W)	4197 ± 667	4185 ± 712	4134 ± 686	4060 ± 682	1,48
t.(PP-PROPULSIÓN) (%)	84,2 ± 3,9	84,1 ± 3,8	84,6 ± 3,0	85,0 ± 3,0	1,19
*** p < 0,001; ** p < 0,01; * p< 0,05; ^1,2 3 indica las diferentes significaciones entre las condiciones (p<0,05).

En la tabla 2 se presentan los datos de tendencia central y nivel de significación de las variables analizadas para el segundo salto. Con respecto a las variables temporales, sólo han existido ciertas diferencias estadísticamente significativas en el tiempo utilizado en la fase de contramovimiento (t._(CONTRAM.)), siendo menor cuando el salto se realizan sin sobrecarga (0%), con respecto al resto de las situaciones (p<0,05). La velocidad vertical del CM en el instante de tomar contacto para realizar el segundo salto (v_(Y)CM recepción), tiende a reducirse a medida que se incrementa la sobrecarga (p<0,001). La prueba de contrastes aplicada a esta variable, pone de manifiesto que existen diferencias estadísticamente significativas cuando se realiza la comparación múltiple por pares entre todas las situaciones, excepto cuando se comparan los saltos con sobrecargas del 2,5% - 5% de la masa. Similar a los datos presentados para el primer salto, la velocidad vertical del CM en el despegue (v_(Y)CM despegue) tiende a reducirse con el incremento de la carga (p<0,001).

La prueba de contrastes pone de manifiesto que existen diferencias estadísticamente significativas cuando se realiza la comparación múltiple por pares entre todas las situaciones, excepto cuando se comparan los saltos con sobrecargas de 5% - 7,5% de la masa. No han existido diferencias estadísticamente significativas entre las medias para el pico máximo de potencia durante la fase propulsiva (PP_{(PROPULSIÓN)}), aunque es necesario señalar que los valores de tendencia central tiende a reducirse a medida que se incrementa la carga. No han existido diferencias entre las medias para el resto de las variables analizadas.

Tabla 2.- Estadística descriptiva y análisis de varianza multifactorial (ANOVA de medidas repetidas), para las variables biomecánicas en las cuatro condiciones de caga (0% 2,5%, 5% y 7,5% con respecto a la masa de cada participante) para el segundo salto.

Variables	0% masa^1	2,5% masa^2	5% masa^3	7,5 masa^4	F
t.(CONTRAM) (s)	0,293 ± 0,075	0,324^1 ± 0,093	0,322^1 ± 0,094	0,329^1 ± 0,093	2,83*
t.(PROPULSIÓN) (s)	0,268 ± 0,051	0,275 ± 0,053	0,275 ± 0,053	0,281 ± 0,053	0,70
t.(PREVIO-DESPEGUE) (s)	0,025 ± 0,004	0,027 ± 0,003	0,026 ± 0,004	0,026 ± 0,005	1,67
YCM recepción (m)	1,195 ± 0,081	1,191 ± 0,099	1,198 ± 0,079	1,188 ± 0,082	0,18
v(Y)CM recepción ( m)	-2,881 ± 0,219	-2,819^1 ± 0,236	-2,774^1 ± 0,218	-2,706^1,2,3 ± 0,226	15,60***
YCM despegue (m)	1,222 ± 0,068	1,220 ± 0,075	1,216 ± 0,075	1,209 ± 0,064	0,65
Iv(CONTRAM) (Ns)	205,3 ± 25,7	205,9 ± 26,7	207,4 ± 25,4	207,2 ± 26,3	0,73
v(Y)CM despegue( m)	2,668 ± 0,183	2,599^1 ± 0,200	2,563^1,2 ± 0,181	2,493^1,2 ± 0,219	14,42***
Iv((PROP.+PREVIO-DESP.) (Ns)	190,1 ± 22,6	189,8 ± 24,8	189,7 ± 23,0	191,2 ± 27,0	0,53
PP(PROPULSIÓN) (W)	3869 ± 633	3856 ± 634	3851 ± 586	3816 ± 631	0,12
t.(PP-PROPULSIÓN) (%)	85,2 ± 4,4	85,1 ± 4,4	86,0 ± 3,1	85,8 ± 3,3	0,53
*** p < 0,001; ** p < 0,01; * p< 0,05; ^1,2,3 indica las diferentes significaciones entre las condiciones (p<0,05).

En la figura 3 se presenta de forma gráfica el análisis comparado entre los dos saltos (Primer salto y Segundo salto) en las cuatro condiciones experimentales (0%; 2,5%; 5% y 7,5% de la masa corporal), para las siguientes variables: a) Velocidad vertical en el despegue (v_(Y)CM despegue), b) Tiempo de propulsión (t._{(PROPULSIÓN)}) y c) Pico máximo de potencia alcanzado durante la fase de propulsión (PP_{(PROPULSIÓN)}). De los datos expuestos se puede afirmar que la velocidad vertical del CM en el despegue ha sido mayor para el primer salto en todas las condiciones de carga. Sin embargo, el tiempo medio utilizado para la fase de propulsión (t._{(PROPULSIÓN)}), ha sido superior para el segundo salto en todas las condiciones de carga. Finalmente, el pico máximo de potencia alcanzado durante la fase propulsiva, ha sido superior para el primer salto en todas las condiciones de carga.

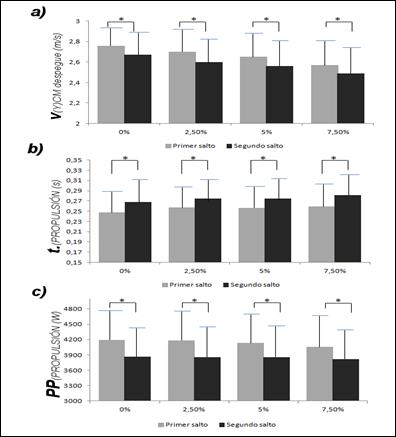
Figura 3. Análisis gráfico comparado entre los dos saltos (Primer salto y Segundo salto) en las cuatro condiciones experimentales (0%; 2,5%; 5% y 7,5%), para la Velocidad vertical en el despegue (v_{(Y)CM despegue)}) (a); el tiempo de propulsión (t._{(PROPULSIÓN)}) (b) y el pico máximo de potencia alcanzado durante la fase de propulsión (PP_{(PROPULSIÓN)}) (c).

DISCUSIÓN

En el primer salto, el tiempo medio utilizado para frenar el contramovimiento (t._{(CONTRAM.-FINAL)}), tiende a incrementarse a medida que se incrementa la carga, aunque sólo han existido ciertas diferencias estadísticamente significativas para los saltos realizados con una sobrecarga del 7,5% de la masa corporal. Considerando que la máxima velocidad vertical negativa del CM ha sido similar en todas las condiciones (v_(Y)CM en t_NV, ver tabla 1), el incremento del tiempo para frenar el movimiento del CM hacia abajo (fase excéntrica) debe de obedecer a la necesidad de aumentar el impulso vertical de frenado, como consecuencia del incremento de la masa desplazada.

El análisis temporal para el segundo salto es similar al descrito para el primero, aunque las causas podrían ser diferentes. Así, el tiempo utilizado para la fase de contramovimiento (t._(CONTRAM.)) es más reducido para los saltos realizados con su propia masa (0%), con respecto a los realizados con cualquiera de las otras cargas. Sin embargo, la velocidad vertical negativa del CM, al inicio de esta fase, es menor a medida que se incrementa carga (v_(Y)CM recepción, ver tabla 2). Este hecho tiene una explicación física simple: A partir de la velocidad de despegue el primer salto (v_(Y)CM despegue, ver tabla 1), es posible conocer que la altura media alcanzada por el CM durante el vuelo tiende a reducirse a medida que se incrementa la carga (0,388 m¸ 0,371 m, 0,359 m, 0,336 m, para 0%, 2,5%, 5% y 7,5%, respectivamente). Al reducirse la altura alcanzada por el CM durante el vuelo del primer salto, también se reducirá la altura de caída para el segundo salto. Así, siendo la posición del CM, en el instante de la recepción, similar para todas las cargas (Y_CM recepción, ver tabla 2), la velocidad vertical negativa en la recepción también se verá reducida.

Sin embargo, no han existido diferencia significativas en el impulso vertical desarrollado durante la fase de contramovimiento (Iv_(CONTRAM), ver tabla 2), lo que nos permite sugerir que la reducción del tiempo de la fase de contramovimiento cuando se desplaza la propia masa (0%), provocará un cierto incremento de la fuerza neta vertical (F_(Z)), con respecto al uso de sobrecargas. Desde una perspectiva muscular, también es posible justificar este aumento de F_(Z) durante la fase de contramovimiento en la condición 0%. Así, la mayor velocidad vertical negativa del CM en el instante de la recepción, producirá un cierto incremento de la velocidad de estiramiento de la musculatura y, consecuentemente, la fuerza excéntrica que puede producir la musculatura implicada en el contramovimiento se verá incrementada (Komi, 1984). Según lo expuesto, podríamos concluir que el menor tiempo utilizado durante la fase de contramovimiento es como consecuencia de haber partido desde una mayor altura previa y no por efecto de las sobrecargas.

Una de las aportaciones más relevantes de esta investigación está relacionada con la velocidad vertical del CM en el despegue (v_(Y)CM despegue). Esta variable se ha reducido con el incremento de la masa en los dos saltos. Desde una perspectiva puramente mecánica, según la siguiente expresión: v_(Y)CM =(I_{V(PROP.+PREVIO-DESP.)}/m), la velocidad vertical en el despegue está relacionada con el impulso vertical y la masa desplazada. Considerando que el impulso vertical (Iv_{(PROP.+PREVIO-DESP.)} ) ha sido similar en todas las condiciones de carga (ver tablas 1 y 2) y la masa desplazada se incrementa un 2,5% en cada condición, la velocidad vertical al final del impulso de propulsión (v_(Y)CM despegue), debería reducirse ese mismo porcentaje. Efectivamente, los datos expuestos confirman que, con el incremento de la carga del 2,5% para cada condición, la velocidad vertical se reduce una media del 2,25%, en el primer salto y de 2,20% en el segundo (ver tabla 1 y 2). Por ello, podríamos afirmar que el impulso vertical permanece similar en todas las condiciones, mientras que la velocidad vertical del CM se reduce en un porcentaje similar al incremento de las carga, coincidiendo con McBride, y cols., (2010).

El pico de potencia durante la fase propulsiva (PP_{(PROPULSIÓN)}) ha sido uno de los indicadores más utilizados para determinar el rendimiento de los saltos verticales, así como el más utilizado para poner de manifiesto que, en los saltos verticales, la carga optima es el propio cuerpo (Cormie y cols., 2007b; Cormie, y cols., 2008; Jaric y Markovic, 2009; McBride, y cols., 2010). Sin embargo, en esta investigación no se han encontrado diferencias significativas en el PP_{(PROPULSIÓN)} en ninguno de los dos saltos (ver tablas 1 y 2). Estas discrepancias pueden estar motivadas por el tipo de salto utilizado y los incrementos de carga. Mientras que en las investigaciones precedentes se han utilizado saltos desde cuclillas (SJ) o utilizando el contramovimiento sin acción de brazos (CMJ con limitación segmentaria), en esta investigación se han utilizado dos saltos máximos consecutivos y con acción segmentaria libre, lo que modifica el carácter de la fuerza desplazada, al tenerse en cuenta la inercia de la masa segmentaria.

Pero, quizás el factor más significativo que justificaría estas discrepancias sería el incremento de la masa para cada condición. Mientras que en las investigaciones expuestas, los incrementos de las cargas son relativamente altos (entre 5-20 Kg o el 20% del 1TRM), en esta investigación, el incremento medio ha sido de 3,5 Kg (2,5% de la masa). Consideramos que el (PP_{(PROPULSIÓN)}) puede ser un buen indicador cuando se comparan saltos manteniendo constante la masa o utilizando incrementos relativamente altos de sobrecarga, mientras que no tiene la suficiente sensibilidad cuando se trata de incrementos de cargas ligeras, donde la velocidad vertical en el despegue puede parece ser un indicador más fiable. Nuestros datos son coincidentes con las aportaciones de Driss y cols., (2001), al poner de manifiesto que las cargas ligeras no tienen efecto sobre el PP_{(PROPULSIÓN)} en deportistas entrenados.

Nuestros datos, tampoco confirman las aportaciones de Fitts y Widick (1996) y Shoepe, y cols., (2003), cuando ponen de manifiesto que la adaptación muscular a las cargas pesadas, provocan un desplazamiento del PP_{(PROPULSIÓN)}. En este sentido, el tiempo en que se produce el pico máximo de potencia durante la fase propulsiva ha sido similar para los dos saltos y en todas las condiciones (t._{(PP-PROPULSIÓN)}, ver tablas 1 y 2). Quizás las explicaciones a esta discrepancia también estén motivadas por los incrementos reducidos de las cargas y el tipo de salto, especialmente, al considerar la relación que tiene el tiempo en que se produce el máximo pico de fuerza con la coordinación segmentaria durante el movimiento.

El análisis comparado entre los dos saltos, pone de manifiesto que el tiempo de propulsión (t._{(PROPULSIÓN)}) se incrementa en el segundo salto para las cuatro condiciones de carga, mientras que la velocidad vertical en el despegue (v_(Y)CM despegue) se reduce. En consecuencia, el pico de potencia durante la fase propulsiva (PP_{(PROPULSIÓN)}) ha sido inferior en el segundo salto para todas las condiciones de carga (ver figura 2). Estos resultados podrían tener su explicación en el impulso de frenado que es necesario desarrollar para invertir la velocidad vertical al caer desde alturas superiores a 0,35 m, lo que coincide con las aportaciones de Bobbert, y cols., (1987) y Peng (2011) cuando señalan que los saltos verticales realizados a partir de altura de caída, entre 0,4 y 0,5 m, o superiores, no producen beneficios sobre fase propulsiva del salto vertical.

CONCLUSIONES Y APLICACIÓN PRÁCTICA

Cuando se utilizan sobrecargas ligeras en los saltos verticales (2,5%; 5% y 7,5% de la masa corporal), el impulso vertical (IV_{(PR0P+PREVIO-DESP)}) y el pico de potencia (PP_{(PROPULSIÓN)}), no varían. Sin embargo, la velocidad de despegue del CM (v_(Y)CM despegue) se reduce un porcentaje similar al incremento de la carga. Estos resultados sugieren la escasa sensibilidad que tiene el impulso vertical y el pico de potencia como indicadores del rendimiento de los saltos verticales cuando se utilizan cargas ligeras y acción libre de los segmentos (acción de brazos).

Cuando se utilizan sobrecargas inferiores al 5% de la masa corporal, el impulso vertical (IV_{(PR0P+PREVIO-DESP)}) y el tiempo de ejecución, en todas sus fases (t_{(CONTRAM-FINAL),} t_{(PROPULSIÓN)} y t_{(PREVIO-DESPEGUE)}), no varían, mientas que la velocidad final del CM (v_(Y)CM despegue) tiende a reducirse en una proporción similar al incremento de la carga. Según estos resultados, podríamos sugerir que, el entrenamiento con sobrecargas inferiores al 5% de la masa corporal, supone aplicar la misma fuerza y no modificar la secuencia temporal de participación segmentaria, mientras que los objetivos pretendidos cambian al reducirse la velocidad final del CM. Así, consideramos que este entrenamiento podría constituir un estímulo neuromuscular para la acción muscular, sin que se vea afectada la coordinación de los movimientos explosivos complejos.

Es necesario ser cautos con el uso de sobrecargas por encima del 5% de la masa corporal, donde el tiempo de la fase contramovimiento tiende a incrementarse, lo que implica un incremento del tiempo de batida y, consecuentemente, una reducción de su eficacia en actividades dinámicas como correr o saltar. Esta misma cautela deberíamos tener al generalizar estos resultados a otras poblaciones diferentes a las que representa la muestra utilizada en esta investigación.

REFERENCIAS BIBLIOGRÁFICAS

Aragón-Vargas, L.F. (2000). Evaluation of four vertical jump tests: Methodology, reliability, validity and accuracy. Measurement in Physical Education and Exercise Science, 4, 215–228.

https://doi.org/10.1207/S15327841MPEE0404_2

Bobbert, M.F., Huijing, P., y van Ingen Schenau, G.J. (1987). Drop jump II. The influence of dropping height on the biomechanics of jumping. Medicine and Science in Sports and Exercise, 19, 339–346. PMid:3657482

Clark, K.P., Stearne, D.J., Walts, C.T., y Miller, A.D. (2010). The longitudinal effects of resisted sprint training using weighted sleds vs. weighted vests. Journal of Strength and Conditioning Research, 24(12), 3287-3295.

https://doi.org/10.1519/JSC.0b013e3181b62c0a PMid:19996786

Cormie, P., McBride, J.M., y McCaulley, G.O. (2008). Power-time, force-time, and velocity-time curve analysis during the jump squat: Impact of load. Journal of Applied Biomechanics, 24, 112–120. https://doi.org/10.1123/jab.24.2.112 PMid:18579903

Cormie, P., McCaulley, G.O., y McBride, J.M. (2007a). Validation of power measurement in dynamic lower body resistance exercise. Journal of Applied Biomechanics, 23, 112–127. https://doi.org/10.1123/jab.23.2.103

Cormie, P., McCaulley, G.O. Triplett, T., y McBride, J.M. (2007b). Optimal loading for maximal power output during lower-body resistance exercises. Medicine and Science in Sports and Exercise, 39, 340-349.

https://doi.org/10.1249/01.mss.0000246993.71599.bf. PMid:17277599

Cronin, J., Hansen, K., Kawamori, N., y McNair, C. (2008). Effects of weighted vest and sled towing on sprint kinematic. Sports Biomechanics, 7(2), 160-172. https://doi.org/10.1080/14763140701841381 PMid:18610770

De Leva, P. (1996). Adjustments to Zatsiorsky-Seluyanovs segment inertia parameters. Journal of Biomechanics. 29(9), 1223-1230.https://doi.org/10.1016/0021-9290(95)00178-6

Driss, T., Vandewalle, H., Quievre, J., Miller, C., y Monod, H. (2001). Effects of external loading on power output in a squat jump on a force platform: a comparison between strength and power athletes and sedentary individuals. Journal of Sports Sciences, 19, 99–105. https://doi.org/10.1080/026404101300036271 PMid:11217015

Dugan E.L., Doyle T.L., Humphries B., Hasson C.J., y Newton R.U. (2004). Determining the optimal load for jump squats: a review of methods and calculations. Journal of Strength and Conditioning Research, 18(3), 668–732. https://doi.org/10.1519/1533-4287(2004)18<668:dtolfj>2.0.co;2

Faigenbaum, A.D., McForland, J.E., Shwerdtman, J.A., Ratamess N.A., Kang J., y Hoffman, J.R. (2006). Dynamic warm protocols, with and without a weighted vest, and fitness performance in high school female athletes. Journal of Atletic Training, 41(4), 357-363. PMid:17273458 PMCid:PMC1748418

Feltner, M.E., Bishop, E.J., y Perez, C.M. (2004). Segmental and kinetic contributions in vertical jumps performed with and without an arm swing. Research Quarterly for Exercise and Sport, 75, 3, 216-230. https://doi.org/10.1080/02701367.2004.10609155 PMid:15487286

Feltner, M.E., Fraschetti, D.J., y Crisp, R.J. (1999). Upper extremity augmentation of lower extremity kinetics during countermovement vertical jumps. Journal of Sports Sciences, 17, 449–466. https://doi.org/10.1080/026404199365768 PMid:10404494

Fitts, R.H., y Widrick, J.J. (1996). Muscle mechanics: adaptations with exercise-training. Exercise and Sport Sciences Reviews, 85, 427–73. https://doi.org/10.1249/00003677-199600240-00016

Gutiérrez-Dávila, M.; Gutiérrez Cruz, C., Garrido, J.M., y Giles F.J. (2012). Efecto de la restricción segmentaria en los test de salto vertical CMJ. Archivos de Medicina del Deporte. XXV(147), 527-535.

Hara, M., Shibayama, A., Takeshita, D., y Fukashiro, S. (2006). The effect of arm swing on lower extremities in vertical jumping. Journal of Biomechanics, 39, 2503-2511. https://doi.org/10.1016/j.jbiomech.2005.07.030 PMid:16168998

Jaric, S., y Markovic, G. (2009). Leg muscle design: the maximum dynamic output hypothesis. Medicine & Science in Sports Exercise, 41, 780–787.

https://doi.org/10.1249/MSS.0b013e31818f2bfa PMid:19276856

Kaneko, M., Fuchimoto, T., Toji, H., y Suei, K. (1983). Training effect of different loads on the force–velocity relationship and mechanical power output in human muscle. Scandinavian Journal Sports Sciences, 5, 50–55.

Khlifa, R., Aouadi, R., Hermassi, S., Chelly, M.S., Jlid, M.C., Hbacha, H., y Castagna, C. (2010). Effects of a plyometric training program with and without added load on jumping ability in basketball players. Journal of Strength and Conditioning Research, 24(11), 2955-2966.

https://doi.org/10.1519/JSC.0b013e3181e37fbe PMid:20938357

Komi, P.V. (1984). Physiological and biomechanical correlates of muscle function: Effects of muscle structure and stretch-shortening cycle on force and speed. Exercise and Sport Sciences Reviews, 12, 81-121. https://doi.org/10.1249/00003677-198401000-00006 PMid:6376140

Lees, A., Vanrenterghem, J., y De Clercq, D. (2004). Understanding how an arm swing enhances performance in the vertical jump. Journal of Biomechanics, 37, 1929-1940.

https://doi.org/10.1016/j.jbiomech.2004.02.021 PMid:15519601

Markovic, G., y Jaric, S. (2007). Positive and negative loading and mechanical output in maximum vertical jumping. Medicine and Science in Sports and Exercise, 39(10), 1757–1764.

https://doi.org/10.1249/mss.0b013e31811ece35 PMid:17909403

McBride, J.M., Kirby, T.J., Hainess, T.L., y Skinner, J. (2010). Relationship between relative net vertical impulse and jump height in jump squats performed to various squat depths and with various loads. International Journal of Sports Physiology and Performance, 5, 484-496. https://doi.org/10.1123/ijspp.5.4.484

Peng, H.T. (2011). Changes in Biomechanical properties during drop jumps of incremental height. Journal of Strength and Conditioning Research, 25(9), 2510-2518. https://doi.org/10.1519/JSC.0b013e318201bcb3

PMid:21869631

Schmidt R.A., y Lee, T.D. (2011). Motor control and learning: A behavioral emphasis (5 th ed.). Champain, IL: Human Kinetics.

Shoepe, T.C., Stelzer, J.E., Garner, D.P., y Widrick, J.J. (2003) Functional adaptability of muscle fibers to long-term resistance exercise. Medicine & Science in Sports & Exercise, 35(6), 944–951. https://doi.org/10.1249/01.MSS.0000069756.17841.9E PMid:12783042

Stone, M.H., O'Bryant H.S., McCoy, L., Coglianese, R., Lehmkuhl, M., y Schilling, B. (2003). Power and maximum strength relationships during performance of dynamic and static weighted jumps. Journal of Strength and Conditioning Research, 17(1), 140–147. https://doi.org/10.1519/00124278-200302000-00022

Thompsen, A.G., Kackley, T., Palumbo, M.A., y Faigenbaum, A.D. (2007). Acute effects of different warm-up protocols with and without a weighted vest on jumping performance in athletic women. Journal of Strength and Conditioning Research, 21(1), 52-56. https://doi.org/10.1519/00124278-200702000-00010 PMid:17313270

Wallace, B.J., Kernozek, T.W., Write, J.M., Kline, D.E., Wright, G.A., Peng, H., y Huang, C. (2010). Quantification of vertical ground reaction forces of popular bilateral plyometric exercises. Journal of Strength and Conditioning Research, 24(1), 207-212 https://doi.org/10.1519/JSC.0b013e3181c3b841 PMid:19924006

Winter, D.A. (1990). Biomechanics and Motor Control of Human Movement (2nd ed.). New York: Wiley Interscience.

Wood, G.A., y Jennings, L.S. (1979). On the use of spline functions for data smoothing. Journal of Biomechanics, 12, 477-479. https://doi.org/10.1016/0021-9290(79)90033-2

Zatsiorsky, V.M., y Seluyanov, N.V. (1983). The mass and inertial characteristics of the main segments of the human body. In: Biomechanics VIII-B. Matsui, H. and K. Kobayashi (Eds) Champaign, I.L: Human Kinetics, 1152-1159.

Número de citas totales / Total references: 32 (100%)

Número de citas propias de la revista / Journal’s own references: 0 (0%)

Rev.int.med.cienc.act.fís.deporte - vol. 16 - número 64 - ISSN: 1577-0354