Buendía-Lozada,
E.R.P; Cruz-Gómez, M.A.; Flores-Chico, B; Aguilar-Enríquez, R.I.;
Villagrán-Arroyo, E.I.; Sánchez-Flores, O. y López-de-la-Rosa, L.E. (2017).
Ecuaciones de predicción de pliegues cutáneos en escolares / Prediction Equations
of Skinfold in Children of Primary School. Revista Internacional de Medicina y
Ciencias de la Actividad Física y el Deporte vol. 17 (65) pp. 27-41. Http://cdeporte.rediris.es/revista/revista65/artecuaciones787.htm
Buendía-Lozada,
E.R.P; Cruz-Gómez, M.A.; Flores-Chico, B; Aguilar-Enríquez, R.I.;
Villagrán-Arroyo, E.I.; Sánchez-Flores, O. y López-de-la-Rosa, L.E. (2017).
Ecuaciones de predicción de pliegues cutáneos en escolares / Prediction Equations
of Skinfold in Children of Primary School. Revista Internacional de Medicina y
Ciencias de la Actividad Física y el Deporte vol. 17 (65) pp. 27-41. Http://cdeporte.rediris.es/revista/revista65/artecuaciones787.htm
DOI: http://dx.doi.org/10.15366/rimcafd2017.65.002
ORIGINAL
ECUACIONES DE PREDICCIÓN DE
PLIEGUES CUTÁNEOS EN ESCOLARES
PREDICTION
EQUATIONS OF SKINFOLD IN CHILDREN OF PRIMARY SCHOOL
Buendía-Lozada,
E.R.P.1; Cruz-Gómez, M.A.2; Flores-Chico, B.3;
Aguilar-Enríquez, R.I.4; Villagrán-Arroyo. E.I.5;
Sánchez-Flores, O.6; López-de-la-Rosa, L.E.7
1 Facultad de
Cultura Física, Benemérita Universidad Autónoma de Puebla (México), buendiaenr@gmail.com
2 Facultad de
Ingeniería, Benemérita Universidad Autónoma de Puebla (México), marco.cruz@correo.buap.mx
3 Facultad de
Cultura Física, Benemérita Universidad Autónoma de Puebla (México),
4 Facultad de
Cultura Física, Benemérita Universidad Autónoma de Puebla (México), Aguilar.enriquez@hotmail.com
5 Facultad de
Ingeniería, Benemérita Universidad Autónoma de Puebla (México), iram.villagran@correo.buap.mx
6 Facultad de
Ingeniería, Benemérita Universidad Autónoma de Puebla (México), oscar.sanchezflores@correo.buap.mx
7 Facultad de
Cultura Física, Benemérita Universidad Autónoma de Puebla (México), dlrosa.luise@gmail.com
AGRADECIMIENTOS
Este trabajo
ha contado con la financiación de PROMEP de la Secretaria de Educación Pública
de México, en su convocatoria de Fortalecimiento de Cuerpos Académicos.
Código
UNESCO / UNESCO code: 5899 Otras especialidades (Educación Física y
Deporte) / Other specialties (Physical Education and Sports)
Clasificación
del Consejo de Europa / Council of Europe classification: 3.
Biomecánica del deporte / Biomechanics of sport
Recibido 9 de mayo de
2014 Received May 9, 2014
Aceptado 26 de mayo
de 2015 Accepted may 26, 2015
RESUMEN
El objetivo
de este trabajo es crear ecuaciones que estimen las medidas de los pliegues
cutáneos para escolares de 6 a 13 años de edad. Como resultado se obtuvieron
catorce ecuaciones que estiman algunos pliegues cutáneos. Las ecuaciones se
validaron con muestras aleatorias de 479 niñas y 541 niños del estado de Puebla
y otras 2 muestras aleatorias del estado de Veracruz con 155 niñas y 146 niños
respectivamente; las mediciones directas se realizaron con la metodología y
unidades ISAK (International Society for the Advancement of Kinanthropometry).
PALABRAS
CLAVE:
Antropometría, Biomecánica deportiva, Tecnología Digital, Pliegues cutáneos.
ABSTRACT
The aim of this paper
is to create equations that predict the skinfold measures for school children 6
to 13 years old. Fourteen resulting equations were derived to estimate some
measures of skinfold. The equations were validated with random samples of 479
girls and 541 boys in the state of Puebla and 2 other random samples of the
state of Veracruz with 155 girls and 146 boys respectively; direct measurements
were performed with the methodology and units ISAK (International Society for
the Advancement of Kinanthropometry.
KEYWORDS: anthropometry, biomechanics sports,
digital technology, skinfold thickness.
INTRODUCCIÓN
El
desarrollo de la niñez puede ayudarnos a conocer las particularidades de los
seres humanos en sus diferentes actividades, genero, edad y a corto, mediano y
largo plazo, así como qué características tienen las generaciones desde
diferentes perspectivas (koutedakis, 2009)
Tomando en
cuenta que, los datos antropométricos se pueden clasificar en dos tipos:
distancia lineal y la circunferencia; que la parte lineal se define como la
distancia entre dos puntos de referencia anatómicos (landmarks), y que la parte
circunferencia se define como la longitud que se puede cerrar alrededor de la
parte (segmento corporal) en el lugar predefinido (Sheng-Fuu, Shih-Che, &
Kuo-Yu, 2010), y que, realizar dichas mediciones antropométricas, toma mucho
tiempo y dinero al usar metodologías estándares (Bastos Moreira, 2008) (Wang,
Wu, Lin, Yang, & Lu, 2007), es deseable que existieran alternativas de
medición que estén validadas.
Bajo esta
perspectiva, se tiene como objetivo crear un grupo de ecuaciones que puedan
estimar el tamaño de los pliegues cutáneos Tríceps (PTRI), Subscapular (PSUB),
Bíceps (PBI), Cresta Iliaca (PCE), Supra espinal (PSE), Muslo Frontal (PMF),
Pierna Media (PPM) para niñas y niños escolares de 6 a 13 años de edad.
MATERIALES Y
MÉTODOS
PARTICIPANTES
El estudio
fue realizado en el municipio de Puebla de la ciudad de Puebla en México,
tomado una muestra aleatoria de escuelas primarias urbanas públicas y privadas
de (eduPortal.com.mx, 2011), se tomaron muestras aleatorias de 705 niñas (tabla
1) y 629 niños (tabla 2) para crear las ecuaciones de regresión múltiple, y se
validaron estas ecuaciones con 479 niñas (tabla 3) y 541 niños (tabla 4) de las
mismas muestras correspondientes, las mediciones directas se realizaron en
junio de 2012 en sus escuelas; así mismo, se seleccionaron al azar de 13
escuelas primarias urbanas, públicas y privadas del estado de Veracruz, del
municipio de Veracruz, 146 niños (tabla 5) y 155 niñas (tabla 6) para validar
las ecuaciones con muestras diferentes, estas mediciones directas se realizaron
el 22 de mayo de 2013 en sus escuelas.
A todas las
niñas y niños se les midió Peso (PESO), Estatura (EST) con tracción, los
pliegues: Tríceps (PTRI), Subscapular (PSUB), Bíceps (PBI), Cresta iliaca
(PCE), Supra espinal (PSE), Abdominal, Muslo frontal (PMF), Pantorrilla Media
(PPM); las circunferencias: Circunferencia cintura mínima, Circunferencia
glútea, Circunferencia brazo relajado (CBRAZOREL), Perímetro cintura mínimo
(CCINTURAMIN), Circunferencia brazo flexionado y tenso, Perímetro Pantorrilla
Máximo (CPIERNAMAX); los diámetros: humero (DHUMER), fémur (DFEMUR); de acuerdo
a ISAK (International Society for the Advancement of Kinanthropometry) para
tener un método estándar en las mediciones, y se pidió su fecha de nacimiento
(EDAD) requerida para calcular la edad cronológica.
Tabla 1. Características de
las niñas de estudio para construir las ecuaciones, n=705
|
Variable |
Media (Desviación estándar) |
Mediana |
Mínimo – máximo |
|
Peso (Kg) |
34,08156 (11,79409) |
32,5 |
11,5-81,5 |
|
Estatura (cm) |
135,2804 (13,02719) |
135,6 |
104,6-177 |
|
Pliegue Tríceps (mm) |
12,38525 (4,411232) |
11,75 |
2,3-30,1 |
|
Pliegue Subescapular (mm) |
10,52156 (5,236291) |
8,75 |
3,5-37 |
|
Pliegue Bíceps (mm) |
8,356028 (3,884591) |
7,5 |
2,5-26,05 |
|
Pliegue Cresta Iliaca (mm) |
15,01695 (7,196236) |
13,75 |
3-39 |
|
Pliegue Supra espinal (mm) |
11,87035 (6,673433) |
10 |
0,5-38 |
|
Pliegue Muslo Frontal (mm) |
17,02993 (6,794842) |
15,75 |
5,25-61 |
|
Pliegue Pantorrilla Media (mm) |
12,45 (5,802209) |
11 |
3,25-41,5 |
|
Perímetro Brazo Relajado (cm) |
21,45938 (3,566636) |
21,2 |
7-35,25 |
|
Perímetro Cintura Mínimo (cm) |
61,77688 (9,596387) |
60,8 |
18-97,55 |
|
Perímetro Pantorrilla Máximo (cm) |
27,69652 (5,253093) |
27,25 |
2,5-93-15 |
|
Diámetro Humero (cm) |
5,376397 (1,247697) |
5,3 |
3,7-34,25 |
|
Diámetro Fémur (cm) |
8,023362 (3,12044) |
7,9 |
4,55-88 |
Tabla 2. Características de
las niños de estudio para construir las ecuaciones, n=629
|
Variable |
Media (Desviación estándar) |
Mediana |
Mínimo – máximo |
|
Peso (Kg) |
40,47751 (11,05549) |
39 |
15-81 |
|
Estatura (cm) |
136,3177 (12,84677) |
136 |
107,95-175-4 |
|
Pliegue Tríceps (mm) |
11,87179 (4,998682) |
11 |
4-32,5 |
|
Pliegue Subescapular (mm) |
9,704928 (5,744996) |
7,25 |
1-36,5 |
|
Pliegue Bíceps (mm) |
7,640223 (3,960186) |
6,5 |
2-21,5 |
|
Pliegue Cresta Iliaca (mm) |
14,24236 (8,438113) |
11,75 |
2-37,75 |
|
Pliegue Supra espinal (mm) |
11,34603 (7,707051) |
8,5 |
2,5-46 |
|
Pliegue Muslo Frontal (mm) |
15,01285 (6,431181) |
13,75 |
3-35,5 |
|
Pliegue Pantorrilla Media (mm) |
11,70715 (6,015475) |
10 |
2,5-35,25 |
|
Perímetro Brazo Relajado (cm) |
21,31717 (3,720032) |
21 |
6,8-33,45 |
|
Perímetro Cintura Mínimo (cm) |
63,64308 (10,87881) |
62 |
5,7-94,35 |
|
Perímetro Pantorrilla Máximo (cm) |
28,01514 (4,116762) |
27,775 |
15-47,7 |
|
Diámetro Humero (cm) |
5,601308 (0,6493822) |
5,55 |
3,7-9,5 |
|
Diámetro Fémur (cm) |
8,416608 (0,8390165) |
8,4 |
5,5-11,05 |
Las tablas 3
y 4 describen las características de las muestras del estado de Puebla, para
validar las ecuaciones de estimación de pliegues cutáneos con las mismas personas
de las muestras con que se crearon las ecuaciones.
Tabla 3. Características de
las niñas donde las nuevas ecuaciones fueron validadas, n=479
|
Variable |
Media (Desviación estándar) |
Mediana |
Mínimo – máximo |
|
Peso (kg) |
33,53184 (11,62495) |
31,4 |
12,2-80,8 |
|
Estatura (cm) |
134,9477 (13,05043) |
134 |
106,7-174 |
|
Pliegue Tríceps (mm) |
12,36897 (4,427739) |
11,5 |
4-28,25 |
|
Pliegue Subescapular (mm) |
10,29151 (5,0362) |
9 |
3-30,05 |
|
Pliegue Bíceps (mm) |
8,242034 (4,339225) |
7,25 |
3-55 |
|
Pliegue Cresta Iliaca (mm) |
14,65273 (7,000449) |
14 |
3,5-38 |
|
Pliegue Supra espinal (mm) |
11,40734 (6,436997) |
10 |
2,5-35,5 |
|
Pliegue Muslo Frontal (mm) |
16,26572 (6,175563) |
15 |
6-42 |
|
Pliegue Pantorrilla Media (mm) |
12,12275 (5,373995) |
11 |
4-31-5 |
|
Perímetro Brazo Relajado (cm) |
21,28753 (3,80201) |
20,8 |
4-35 |
|
Perímetro Cintura Mínimo (cm) |
61,40818 (9,540226) |
60,5 |
5,5-94 |
|
Perímetro Pantorrilla Máximo (cm) |
27,57715 (4,348333) |
27,1 |
19,25-66-5 |
|
Diámetro Humero (cm) |
5,52804 (3,244278) |
5,3 |
4,05-54 |
|
Diámetro Fémur (cm) |
7,86043 (0,7691566) |
7,85 |
4,8-10,1 |
Tabla 4. Características de
las niños donde las nuevas ecuaciones fueron validadas n=541
|
Variable |
Media (Desviación estándar) |
Mediana |
Mínimo – máximo |
|
Peso (Kg) |
33,52802 (11,24576) |
30,75 |
14,9-81 |
|
Estatura (cm) |
134,5654 (12,58272) |
133,7 |
106,8-173,1 |
|
Pliegue Tríceps (mm) |
11,2768 (4,861312) |
10 |
3,5-31-5 |
|
Pliegue Subescapular (mm) |
9,295833 (5,541476) |
7 |
3-36,05 |
|
Pliegue Bíceps (mm) |
7,560093 (4,117071) |
6,5 |
2-26,1 |
|
Pliegue Cresta Iliaca (mm) |
13,47056 (7,990739) |
11 |
3-48 |
|
Pliegue Supra espinal (mm) |
10,59787 (7,311645) |
7,875 |
2-45,05 |
|
Pliegue Muslo Frontal (mm) |
14,92657 (6,886113) |
13 |
4-58 |
|
Pliegue Pantorrilla Media (mm) |
11,27745 (5,877952) |
10 |
3-41 |
|
Perímetro Brazo Relajado (cm) |
20,89194 (3,611476) |
20,175 |
6,7-35,45 |
|
Perímetro Cintura Mínimo (cm) |
62,57157 (10,61484) |
60,8 |
17,7-101,7 |
|
Perímetro Pantorrilla Máximo (cm) |
27,62028 (4,948647) |
26,8 |
15-69,4 |
|
Diámetro Humero (cm) |
5,650519 (3,504332) |
5,425 |
4-85,7 |
|
Diámetro Fémur (cm) |
8,362565 (1,280854) |
8,3 |
5,6-31,1 |
La tabla 5 y
6 describen las características de las muestras del estado de Veracruz, para
validar las ecuaciones de estimación de pliegues cutáneos con muestras
diferentes de personas y localidad.
Tabla 5. Características de las
niños de Veracruz donde las nuevas ecuaciones fueron validadas n=146
|
Variable |
Media (Desviación estándar) |
Mediana |
Mínimo – máximo |
|
Peso (kg) |
36,83566434 (12,6723332) |
34 |
13,1-92,5 |
|
Estatura (cm) |
136,58 (12,6641149) |
136 |
109-169 |
|
Pliegue Tríceps (mm) |
12,199726 (4,82635572) |
11 |
4-26 |
|
Pliegue Subescapular (mm) |
10,1342466 (6,37072111) |
7,75 |
3-36 |
|
Pliegue Bíceps (mm) |
8,95068493 (4,87834531) |
7,75 |
2,5-28,5 |
|
Pliegue Cresta Iliaca (mm) |
13,0373288 (6,84314428) |
13 |
4-36 |
|
Pliegue Supra espinal (mm) |
10,8684932 (6,86078546) |
9 |
3-38 |
|
Pliegue Muslo Frontal (mm) |
15,9657534 (6,58420108) |
14,5 |
5-42 |
|
Pliegue Pantorrilla Media (mm) |
13,9657534 (5,85090119) |
12,75 |
4-33 |
|
Perímetro Brazo Relajado (cm) |
22,1407534 (4,49833304) |
21,35 |
6,7-36,7 |
|
Perímetro Cintura Mínimo (cm) |
64,5821918 (12,9618351) |
63,5 |
8,6-102 |
|
Perímetro Pantorrilla Máximo (cm) |
28,7541096 (4,98330606) |
28,1 |
16-44,3 |
|
Diámetro Humero (cm) |
6,08275862 (4,62781836) |
5,6 |
4-61 |
|
Diámetro Fémur (cm) |
8,65551724 (0,85500791) |
8,6 |
6,3-10,9 |
Tabla 6. Características de
las niñas de Veracruz donde las nuevas ecuaciones fueron validadas n=146
|
Variable |
Media (Desviación estándar) |
Mediana |
Mínimo – máximo |
|
Peso (kg) |
35,59668874 (12,49581873) |
32,9 |
15,8-73,8 |
|
Estatura (cm) |
135,974342 (13,8005697) |
134,85 |
110-195 |
|
Pliegue Tríceps (mm) |
13,3599342 (4,75722449) |
13 |
2-27 |
|
Pliegue Subescapular (mm) |
10,8888158 (5,67513679) |
9 |
4-34 |
|
Pliegue Bíceps (mm) |
9,81973684 (3,90281679) |
9 |
4-24 |
|
Pliegue Cresta Iliaca (mm) |
14,2703947 (6,39973107) |
14 |
4,5-39 |
|
Pliegue Supra espinal (mm) |
11,7263158 (5,78934749) |
10,25 |
3-29 |
|
Pliegue Muslo Frontal (mm) |
17,55322895 (6,23110742) |
16 |
7,7-41 |
|
Pliegue Pantorrilla Media (mm) |
14,0335526 (5,37181906) |
13 |
6-30 |
|
Perímetro Brazo Relajado (cm) |
21,9677632 (3,85596943) |
21,5 |
8,3-31,9 |
|
Perímetro Cintura Mínimo (cm) |
62,6071053 (10,9749244) |
62 |
6,58-95,4 |
|
Perímetro Pantorrilla Máximo (cm) |
29,7447368 (5,85897635) |
28,6 |
19-52 |
|
Diámetro Humero (cm) |
5,76032895 (3,74592734) |
5,4 |
4,04-51 |
|
Diámetro Fémur (cm) |
8,13440789 (0,86346969) |
8,1 |
4,7-10,5 |
MATERIAL
El equipo de
medición que se utilizo es el ISAK recomienda; Kit antropométrico Rosscraft con
plicómetro Herpenden, báscula digital Microlife, cajón antropométrico Nuevo
León, cinta métrica de metal, antropómetro pequeño o calibrador, hojas de
registro de mediciones, escuadra.
MÉTODOS
Se usó la
metodología de medición y unidades de ISAK (International Society for the
Advancement of Kinanthropometry) para las medidas directas.
La investigación se
ajustó a la Declaración de Helsinki, motivo por el cual hubo niñas y niños que
no quisieron participar; la edad de las niñas y niños fue entre 6 y 13 años y
del primer a sexto grado de educación primaria.
La validación de las
ecuaciones de estimación de pliegues cutáneos se realizó calculando la
repetitividad (B. Mandeville, 2007) y el acuerdo con el coeficiente de
correlación de Pearson, para el caso de comparar las estimaciones con las
medidas directas ISAK de las mismas personas. Para la condición de verificar el
acuerdo con muestra diferente de personas y las ecuaciones de regresión creadas
se usó la gráfica Blant – Altman.
ANÁLISIS
ESTADÍSTICO
Para el caso
de los números aleatorios de los muestreos y análisis de los datos se realizaron
en el Lenguaje R (R Core Team, 2012) (R Core Team, 2013), el ajuste se verificó
con la función plot (fit) para el caso de los residuales. Así para el caso de
la repetitividad de las ecuaciones de estimación de pliegues cutáneos se empleó
el coeficiente concordancia de Lawrence Lin (Lawrence & Lin, 1989), de la
Librería Agreement (Yu & Lin, 2012); las ecuaciones de regresión múltiple
se crearon con la función Im.
La base de
datos se capturo en Excel (Microsoft, 2010)
Para el Cálculo de la
precisión entre dos métodos se usó la formula
![]() (Press
& Fisher, 2008)
(Press
& Fisher, 2008)
RESULTADOS
Con la
muestra de niñas descritas en la tabla 1, se construyeron las ecuaciones de
regresión de la tabla 7.
Tabla 7. Ecuaciones de regresión
para el pronóstico de pliegues cutáneos en niñas de 6 a 13 años de edad de
educación primaria (con unidades de medición ISAK para los parámetros de las
ecuaciones)
|
Ecuaciones para niñas |
R cuadrada Ajustada |
|
(1)
PTRI= -5,03431-EST(0,05117) +CCINTURAMIN(0,08649)
+CBRAZOREL(0,88531) |
0,6206 |
|
(2)
PSUB= -13,59314-EST(0,04737)+
CCINTURAMIN(0,18240) +CBRAZOREL(0,89730) |
0,6937 |
|
(3)
PBI=
(-6,30905)+CBRAZOREL(0,79544)-EDAD(0,25009) |
0,4507 |
|
(4)
PCE= -21,96109+CCINTURAMIN(0,21299)+
CBRAZOREL(1,11002) |
0,6349 |
|
(5)
PSE= -22,97773 + CCINTURAMIN(0,23677) +
CBRAZOREL(1,04481) –EDAD(0,22883) |
0,6762 |
|
(6)
PMF= - 12,03850+ CCINTURAMIN(0,11188) +
CBRAZOREL(1,13412) – EDAD(0,61324)+ CPIERNAMAX(0,10331) + DFEMUR(0,10671) |
0,5057 |
|
(7)
PPM= - 14,34734 + CCINTURAMIN(0,12778) +
CBRAZOREL(1,05928) – EDAD(0,39815) |
0,5872 |
Con la
muestra de niños descritos en la tabla 2, se construyeron las ecuaciones de la
tabla 8.
Tabla 8. Ecuaciones de
regresión para el pronóstico de pliegues cutáneos en niños de 6 a 13 años de
edad de educación primaria (con unidades de medición ISAK para los parámetros
de las ecuaciones).
|
Ecuaciones para niños |
R cuadrada Ajustada |
|
(1)
PTRI= -1,85012 - EST(0,11442)
+CCINTURAMIN(0,07186) +CBRAZOREL(1,16081) |
0,6833 |
|
(2)
PSUB= -7,90235 - EST(0,12206)+ CCINTURAMIN(0,13823)
+CBRAZOREL(1,19386) |
0,7056 |
|
(3)
PBI= -3,85205 - EST(0,04788)+
CBRAZOREL(0,96191) – EDAD(0,25483) |
0,581 |
|
(4)
PCE= -17,04008 – EST(0,13540) + CCINTURAMIN
(0,16752)+ CBRAZOREL(1,83990) |
0,7087 |
|
(5)
PSE= -20,60825- EST(0,07050)+CCINTURAMIN(0,16157)+CBRAZOREL(1,59227)-EDAD(0,27270) |
0,7378 |
|
(6)
PMF= - 5,45435 – EST(0,06822) +
CCINTURAMIN(0,09429) + CBRAZOREL(1,42063)-EDAD(0,65323) |
0,5844 |
|
(7)
PPM= -10,55279 –EST(0,03679)+ CCINTURAMIN
(0,05649) + CBRAZOREL(1,32566) – EDAD(0,46952) |
0,6271 |
Al
contrastar las mediciones directas de las personas de Puebla (tablas 3 y 4)
contra las estimaciones de mediciones de pliegues obtenidos con las ecuaciones
de pronóstico de la misma muestra, se obtienen las tablas 9 y 10, que verifican
las reproductibilidad y confiabilidad de las ecuaciones de estimación de
pliegues cutáneos.
Tabla 9. Residuales
(Mediciones directas=y, Ecuación Pronostico=X), Coeficiente de Concordancia Lawrence-Lin
(L.Lin) y el Coeficiente de Correlación de Pearson en Niñas.
|
Pliegue Cutáneo L-Lin Pearson Residuales |
||
|
(1)
PTRI
|
(2)
PSUB
|
(3)
PBI
|
|
(4)
PCE
|
(5)
PSE
|
(6)
PMF
|
|
(7)
PPM
|
|
|
Tabla 10. Residuales
(Mediciones directas=y, Ecuación Pronostico=X), Coeficiente de Concordancia Lawrence-Lin
(L.Lin) y el Coeficiente de Correlación de Pearson en Niños.
|
Pliegue Cutáneo L-Lin Pearson Residuales |
||
|
(1)
PTRI
|
(2)
PSUB
|
(3)
PBI
|
|
(4)
PCE L.Lin=0,8087 Pearson=0,8146914
|
(5)
PSE L.Lin=0,8331 Pearson=0,8404457
|
(6)
PMF L.Lin=0,7246 Pearson=0,7614115
|
|
(7)
PPM
|
|
|
Las bases de
datos global de Puebla y Veracruz sin ajuste que se usó en este trabajo están
en (Buendía Lozada E.R., 2014).
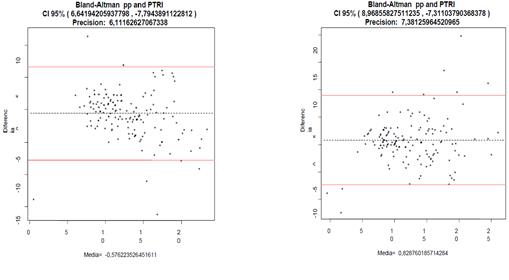
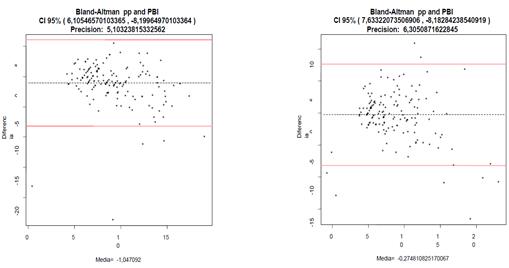
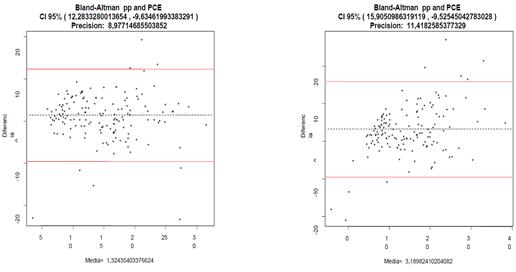
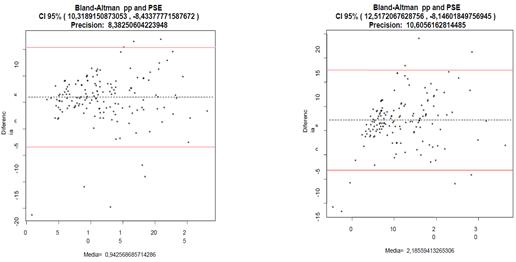
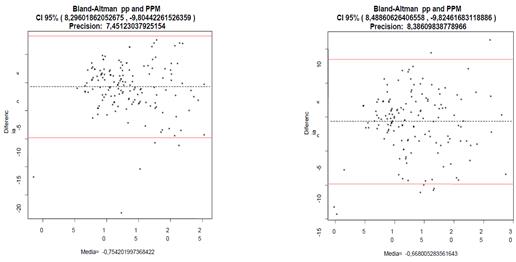
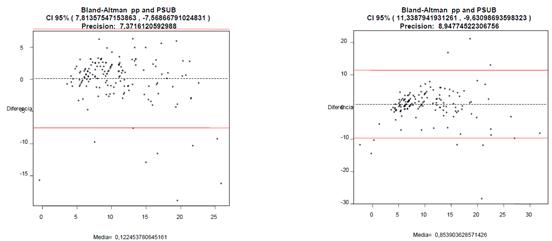
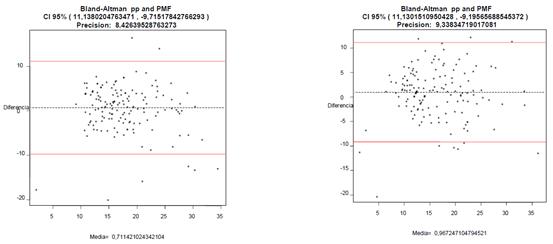
Las gráficas
Blant – Altman de la tabla 11 describen las diferencias y la precisión que se
obtuvieron al usar los datos de las muestras de la tabla 5 y 6 con las
estimaciones de las ecuaciones correspondientes en niñas y niños de Veracruz.
Tabla 11. Blant – Altman en
niñas lado izquierdo y niños del lado derecho (Mediciones directas=Pliegue
corporal correspondiente, Ecuación de estimación de pliegues cutáneos=pp).
|
Niñas |
Niños |
|
|
|
DISCUSIÓN Y
CONCLUSIONES
Las
ecuaciones de la tabla 7 y 8 están validadas para poder estimar medidas de los pliegues
cutáneos: Tríceps (PTRI), Subscapular (PSUB), Bíceps (PBI) con el más bajo
nivel de confianza, Creta Iliaca (PCE), Supra espinal (PSE), Muslo Frontal
(PMF), Pierna Media (PPM); para niñas y niños escolares de 6 a 13 años de edad
en los municipios de Puebla y Veracruz, dan la posibilidad de ampliar su uso en
la Educación Física, ampliando de esta forma las alternativas de medición, tal
como lo sugieren (Bastos Moreira, 2008) (Wang, Wu, Lin, Yang, & Lu, 2007).
Para
aumentar portabilidad de los instrumentos de medición de acuerdo a
(kohlschütter & Herout, 2012), se creó una aplicación de cómputo que usa
fotografías perpendiculares a los segmentos corporales para capturar o
aproximar los parámetros de las ecuaciones de estimación de pliegues cutáneos de
las tablas 7 y 8; para calibrar las mediciones, se debe usar un objeto de
referencia de dimensión conocida, que el software ajusta de la medida en
fotografía a una medida real por regla de tres; calcula la distancia lineal
Euclídea para los diámetros y longitudes, y las circunferencias con un modelo
elíptico perimetral (MathslsFun.com, 2013). Para el caso de los niños necesita
los datos, circunferencia cintura mínima, circunferencia brazo relajado, y para
las niñas: circunferencia cintura mínima, circunferencia brazo relajado,
circunferencia pierna máxima y diámetro de fémur; que se puede calcular
marcando con el apuntador del ratón en los puntos que definen los extremos a
medir de los segmentos corporales en la parte medial correspondiente y para
niños y niñas se necesita capturar su edad, estatura y peso; evitando con este
software ser invasivos con las personas como lo describe (Herianto,Probandari,
& Darmawan, 2010). La aplicación de cómputo AD descrita anteriormente se
encuentra disponible en (Buendía Lozada E. R., 2014), el cual tiene los mismos
problemas potenciales referidos por (kohlschütter & Herout, 2012) y que
requiere de más investigación para mejorarlo.
REFERENCIAS
BIBLIOGRÁFICAS
B. Mandeville.
P. (2007). El coeficiente de correlación de concordancia de Lin. Ciencia UANL, 91-94
Bastos Moreira, S. (2008). The Validity of the photoshop 8 program usage
to obtain anthropometric measurements. Fitness &
performance EISSN 1676-5133, 158-161. https://doi.org/10.3900/fpj.7.3.158.e
Buendía
Lozada, E. R. (28 de Abril de 2014). SourceForge.net. Recuperado el 28 de Abril
de 2014, de Biomechanics, DataBAse dbAnthropometryChildM_xico.xlsx: http://sourceforge.net/projects/biomechanics/files/DataBase/
eduPortal.com.mx.
(13 de junio de 2011). Primarias en Puebla, Puebla, México. Recuperado el 13 de
junio de 2011, de Municipio de Puebla, escuelas públicas y privadas.
eduPortal.com.mx
http://eduportal.com.mx/escuelas/primarias/en/puebla/puebla?pagina=3
Flores H.,
S. (2006). Antropometría, estado nutricio y salud de los niños. Importancia de
las mediciones comparables. Medigraphic Artemisa, 76-75.
Herianto,
Probandari, S., & Darmawan, A. (2010). Development
of digital anthropometric circuferential measurement system based on two dimensional
images. The 11th Asia Pasific Industrial engineering and management
systems conference, 1-6.
Kohlschütter, T., & Herout, P. (2012). Automatic Human Body Parts
Detection in a 2D Anthropometric System. Springer-Verlag Berlin Heidelberg,
536-544. https://doi.org/10.1007/978-3-642-33191-6_53
Koutedakis, Y. (2009). Biomechanics in dance. En
E. R. Buendia L., Bio-Mecánica deportiva (pág. 11). Puebla, México.; Fomento
editorial BUAP.
Lawrence,
I., & Lin, K. (1989). A Concordance Correlation Coefficient to Evaluate
Reproducibility. Biometrics, Vol.45, No. 1, 255-268. https://doi.org/10.2307/2532051.
MathslsFun.com. (2013). Perimeter of an Ellipse. Recuperado
el 1 de julio de 2013, de Perimeter of an Ellipse: http://www.mathsisfun.com/geometry/ellipse-perimeter.html
Microsoft. (2010). Excel. United States.
Preiss, D., & Fisher, J. (2008). A measure of confidence in
Bland-Altman analysis for the interchangeability of methods of measurement.
Journal of Clinical Monitoring and Computing, 257-259. https://doi.org/10.1007/s10877-008-9127-y.
R
Core Team. (29 de Febrero de 2012). R: A Language
and Environment for Statistical Computing. Vienna, Austria.
R Core Team. (25 de Septiembre de 2013). R: A Language and Environment
for Statistical Computing. Vienna, Austria.
Sheng-Fuu, L., Shih-Che, C., & Kuo-yu, C. (2010). The 2D Image-Based
Anthropologic Measurement by using Chinese Medical Acupuncture and Human Body
Slice Model. (IJCSIS) International Journal of Computer Science and Information
Security, 20-29.
Ureña Bonilla, P., Blanco Romero, L., & Salas Cabrera, J. (2015). Calidad
de vida, indicadores antropométricos y satisfacción corporal en un grupo de
jóvenes colegiales. Retos, 62-66.
Wang. M.-J. J., Wu, W.-Y., Lin, K.-C., Yang, S., & Lu, J.-M. (2007).
Automated anthropometric data collection from three-dimensional digital human
models. The international Journal of Advanced Manufacturing Technology,
109-115. https://doi.org/10.1007/s00170-005-0307-3.
Yu,
Y., & Lin, L. (29 de Octubre de 2012). Package
‘Agreement’. Obtenido de The Comprehensive R Archive network, Contributed
Packages: http://cran.r-projetc.org/web/packages/Agreement/Agreement.pdf
Referencias
totales / Total references: (100%)
Referencias
propias de la revista / Journal's own references: 0 (0%)
Rev.int.med.cienc.act.fís.deporte
-
vol. 17 - número 65 - ISSN: 1577-0354