Pic Aguilar, M. y Navarro
Adelantado, V. (2017). La comunicación motriz de tríada y la especificidad de
los juegos motores / Triad Communication and Specificity of Motor Games.
Revista Internacional de Medicina y Ciencias de la Actividad Física y el
Deporte vol. 17 (67) pp. 523-539. Http://cdeporte.rediris.es/revista/revista67/artcomunicacion846.htm
Pic Aguilar, M. y Navarro
Adelantado, V. (2017). La comunicación motriz de tríada y la especificidad de
los juegos motores / Triad Communication and Specificity of Motor Games.
Revista Internacional de Medicina y Ciencias de la Actividad Física y el
Deporte vol. 17 (67) pp. 523-539. Http://cdeporte.rediris.es/revista/revista67/artcomunicacion846.htm
DOI: https://doi.org/10.15366/rimcafd2017.67.009
ORIGINAL
LA COMUNICACIÓN MOTRIZ
DE TRÍADA Y LA ESPECIFICIDAD DE LOS JUEGOS MOTORES
TRIAD COMMUNICATION AND
SPECIFICITY OF MOTOR GAMES
Pic
Aguilar, M.1 y Navarro Adelantado, V.2
1 Profesor de Educación Física en Secundaria. IES Garoé,
Islas Canarias (España) pic.aguilar.90@ull.edu.es
2 Profesor Titular de Universidad. Departamento de
Didácticas Específicas. Universidad de La Laguna (España) vnavarro@ull.edu.es
CÓDIGO UNESCO /
UNESCO code: 6305. Sociología matemática / Sociology Mathematics. 630599. Redes de
comunicación / Communication Networks.
Clasificación
Consejo de Europa / Council of Europa classification: 16. Sociología del
Deporte / Sociology of Sport.
Recibido 5 de mayo de
2015 Received May 5, 2015
Aceptado 26 de julio de
2015 Accepted July 26, 2015
RESUMEN
Se estudian las tríadas desde la
comunicación motriz, con el propósito de a)
identificar los distintos tipos a que da lugar la tríada; b) medir las
diferencias entre los tipos de tríadas estudiados; y c) mostrar con juegos
concretos la viabilidad de los juegos de tríada trasladables a programas. Se
justifican 13 tipos susceptibles de ser viables como juegos motores, que
corresponden a tríadas completas y a tríadas con ausencia de una conexión entre
dos de sus nodos. Se comparan cuatro juegos por medio de cinco indicadores:
roles, interacción intragrupo, interacción intergrupos, emisiones o
recepciones, y valencia positiva o negativa. La comparación evidencia el
comportamiento específico de las tríadas motrices. Los resultados confirman la
viabilidad de los juegos estudiados, y las diferencias relativas entre
antagonismo y solidaridad. Los juegos motores de tríada son una fuente singular
de comunicación motriz y una alternativa pedagógica para los programas de
juegos.
PALABRAS CLAVE: Juego motor,
tríada, red de comunicación, praxiología motriz, educación física
ABSTRACT
Triads are studied from a motor communication point of
view. Our study is aimed at a) identifying the various type that triads
originate; b) measuring the differences among the type of the studied triads;
and c) showing with specific examples the feasibility of triad games
transferred to programs. 13 types are justified as being likely feasible as
motor games. They correspond to complete triads and to triads with one missing
connection between two of its nodes. Four games are compared through five
different proxies: roles, intra-group interaction, interaction among groups,
emissions and receptions, and positive or negative valence. The comparison
demonstrates the specific behavior of motor triads. The results confirm the
feasibility of the studied games and the relative differences between rivalry and
solidarity. Motor games with a triad structure are a singular source of
communication and a pedagogic alternative for game programs.
KEYWORDS: Motor
game, triad, communication network, motor praxeology, physical education
1.
INTRODUCCIÓN
El análisis
de la red de comunicación de tríada, tomando como objeto el juego motor y su
viabilidad en la práctica, ha tenido una atención muy reducida. Nuestra
aportación se centra en el comportamiento específico de la tríada motriz, ante
la interacción motriz antagónica entre tres personas o grupos.
Los juegos motores
de tríada son una rareza del patrimonio lúdico. ¿Por qué son tan escasos los
juegos de tríada? Parlebas (2001, p131) apunta hacia la ‘deportificación’ de
los juegos, como una adaptación del juego al nuevo orden cultural. Así,
entenderíamos cómo la ambigüedad, manifestada en la ambivalencia de la tríada,
es un costo de confusión que la sociedad evita en sus fórmulas lúdicas
(Parlebas, 1988, p.102). Para Bauman (2005, p.12-18), la ambivalencia es un
desafío que nos hacemos para vivir juntos y ayudarnos, frente a la hegemonía de
la cultura objetiva (Robles, 2000, p. 229). El deporte, al negar esta
ambivalencia, representa una fórmula institucionalizada dualista que funciona
con sus propios ordenamientos internos (Puig y Heinemann, 1991). En este contexto de enfrentamiento surge la tríada y su
ambivalencia, como propiedad específica
de las relaciones de comunicación, susceptible de ser matematizada desde la perspectiva
de los juegos deportivos (Parlebas, 1981, 2005a, 2005b, 2005c, 2010, 2011). La
tríada ofrece diversas versiones en su comunicación que no han sido exploradas
desde el punto de vista de los juegos motores, pero parece más apropiado hablar
de distintas tipos, a modo de formas estructurales, ya que no hay para ellos
nuevas condiciones fundamentales que las diferencien socialmente. Iremos
desarrollando estos tipos, según sean sus conexiones y flujos, con los tres equipos
conectados o con ausencia de una
conexión (‘agujero estructural’, Burt,
2004, p.65).
Un campo de aplicación de las tríadas
motrices es la educación física, reconociéndolas como una alternativa al modelo
dominante de carácter deportivo (Navarro, 1995, 2006, 2009); también, las
tríadas traen consigo un mayor enriquecimiento motor de las propuestas de
juegos (alianzas, situaciones-problema), y lo que es más importante: saber cómo
hacerlas jugables. El mundo de los juegos motores solamente se ha interesado
por dos tipos de tríadas (Parlebas, 1981, 1996; Guillemard, Marchal, Parent,
Parlebas y Schmitt, 1988; Navarro, 1995; 2011; Sánchez, 2000), y esta estructura
de comunicación sigue siendo poco común en los programas de juegos.
Para comprender ampliamente el
fenómeno de la tríada, aludiremos a distintos enfoques y a una visión
específica. En primer lugar, partamos de una visión sociocultural de la tríada
y su fenómeno. Como bien dice Parlebas (2005c, p.115), «(…) las estructuras de
los juegos pueden ser también reveladoras de las estructuras sociales (…)
revelan una etnomotricidad específica (…)». Boudon (1980) nos permite
comprender por qué la comunicación dual es hegemónica sobre la comunicación de
tríada, y apunta a que la función principal de la organización social es la
eliminación del efecto perverso.
Desde luego, del desarrollo del juego motor de tríada emerge un conflicto de
intereses en la resolución de situaciones en las que se da un doble contrato
contradictorio. Lèvi-Strauss (1962/1997, p.56-59), al estudiar un juego de los
indios fox en forma de rito de los
muertos y los vivos, encuentra que la victoria en un juego deportivo dual es un
suceso simbólico que favorece en los vencedores un suplemento de vida. En
deporte, salvo alguna excepción (Three sided football, ideado por Asger Jorg), parece más eficiente una fórmula dual, pues
aporta claridad al mensaje para que los jugadores y espectadores comprendan la
situación motriz, quizá por esto el juego social esté de espaldas a la tríada.
Otra visión interesada por la tríada
es la matemática en el contexto de las ciencias sociales. En cuanto a la
utilidad descriptiva de la teoría matemática de juegos para predecir las
conductas lúdicas, Barbut (1967, p.840) alude a la diferencia entre ‘esquema de
causalidad’ y ‘esquema de finalidad’ del juego, y postula insertar en el
análisis matemático las conductas humanas en la acción (p.863). Pero, ¿cómo
incide la previsión matemática en la acción motriz de los juegos de tríada? La
vertiginosa acción motriz, en una situación simultánea de juego de tríada, ¿permite
a los jugadores aplicar su estrategia?
Simmel (1950) fue el primero en
estudiar las interacciones sociales de tres individuos, cuya situación llevaba
aparejada un rol mediador; y consideró la tríada sin coaliciones y más
dependiente de la voluntad del tercer individuo. Para él, la tríada es una
díada más uno. Granovetter (1973, p.1363) denominó ‘tríada prohibida’ a la comunicación
carente de una conexión entre alguno de los tres vértices, y reconoce una
dificultad en uno de los agentes para mantener dos relaciones fuertes, lo que
traería consigo mayores probabilidades de tender puentes en la parte débil (no
conexa o con diferencias de fuerzas). Siguiendo esta línea anterior, Caplow
(1956, 1959/1968) estudió las tríadas y su distribución del poder de partida,
así como la propiedad que atribuye a la tríada: la coalición o alianza. Para él,
las tríadas son de ocho tipos, según este criterio de poder (1968, p.57), y
alude a cómo la fuerza fluctúa durante el desarrollo de las interacciones. Caplow
considera que es fundamental el poder de los individuos para comenzar el
proceso negociador de coaliciones, reduciendo así la tríada originaria a dos
bloques claramente definidos (Esteban y Mayoral, 2011). Parlebas (2011, p.23,9)
discute el planteamiento de Caplow por ser estrictamente cuantitativo,
polarizado, y ligado al poder de cada grupo a semejanza de la economía, cuando
—siguiendo al autor— la tríada nos muestra su desarrollo exitoso en los juegos
deportivos, poniendo en evidencia que el efecto Condorcet (intransitividad
entre tres elementos) se encuentra en la práctica de estos juegos. Es decir, no
es determinante el peso o poder inicial que posee cada equipo en una tríada,
pues los jugadores actúan minimizando estratégicamente sus diferencias de
partida. Otro aspecto a favor de la especificidad lo aporta Flament (1977), al
considerar el peso de la tarea en la comunicación. Y más interesado en el
reparto del poder de las alianzas, Gamson (1961) se ocupa de esta distribución
con la menor cantidad de fuerza (‘coaliciones dominantes más económicas’).
Pero, ¿cómo resolver la alianza? Para
Mills (1953, 1954), los dos miembros de la tríada más activos tendrían mayor
posibilidad de realizar alianzas, con cuatro situaciones entre dos
participantes y el tercero: solidaridad, conflictividad, dominancia, y pugna
frente a la dominancia. Entendemos que el autor describe dos planos; el primero
el de la comunicación (solidaridad y rivalidad), y, el segundo, el de las
diferencias de fuerzas (dominancia, y pugna frente a la dominancia).
Desde el análisis de los juegos
motores, Navarro (1995) aborda la tríada motriz en una investigación
cuasiexperimental, confrontando las diferencias entre un mismo juego jugado de
forma dual o en forma de tríada. El autor advierte de la complejidad de
interacciones e incremento de la densidad entre la versión del juego dual y la
versión del mismo juego practicado en tríada. Más tarde, analiza la
transformación de juegos motores duales en juegos de tríada (Navarro, 2006,
2011).
Hasta aquí, hemos visto importantes
enfoques que nos hacen entender el fenómeno de la tríada. Mirémoslo ahora desde
la comunicación motriz y su lógica interna. La praxiología motriz de Parlebas
(1976, 1981, 1988) constituye una teoría relevante para nuestro propósito, pues
se fundamenta en una perspectiva estructural y sistémica con la que abordar el
estudio de la tríada motriz por medio de conceptos operatorios como ‘comunicación
motriz’, ‘interacción motriz’, ‘rol sociomotor’, y ‘lógica interna’. Además, de
la modelización de los juegos deportivos (mathemasation
structurante, Parlebas, 2005a, p.114) es factible diferenciar el peso del
rol y de sus acciones en los tipos de tríadas, e identificar el motivo de esas
diferencias. La comunicación motriz es aplicada a los juegos mediante la teoría
de grafos con enfoque social (Parlebas, 1988); así, las redes de comunicación
motriz de las tríadas con sus tres vértices o nodos conectados constituyen
redes ambivalentes (situaciones paradójicas). Parlebas (1981, 2005b, 2010)
estudia, entre ellas, un tipo de tríada motriz (‘zorros, gallinas y víboras’)
con la relación A→B→C→A. En conjunto, una tríada motriz posee
una estructura objetiva de red de comunicación que conecta inicialmente a los equipos
de manera negativa (rivalidad), y en la que pueden aparecer episodios de
coalianza (solidaridad); se trata, entonces, de un grafo completo en el que
todas sus aristas están conectadas: A−B, B−C, A−C. Sin
embargo, la tríada varía poderosamente cuando se diversifica el sentido de su
flujo de comunicación (p.e. A↔B, A→C, B→C), y aún más cuando
carece de una conexión.
Hay un subgrupo de tríadas no
exploradas como juegos motores. Nos referimos a las tríadas sin conexión entre
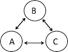
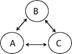
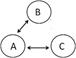
dos de sus nodos, aunque presenten tres elementos (figura 1, tipos 8, 9, 10,
11, 12, 13). Todos estos tipos traen consigo un enfrentamiento
de doble díada (Heider, 1946), pues la ambivalencia no es factible por causa de
la regla y las relaciones que establece. Para Kadushin (2013, p.46-54) la tríada es un verdadero
sistema social, en el que la díada es su unidad más pequeña (2013, p.53).
Podría parecer que los tipos del 8 al 13 no interesan al diseño de juegos
motores en razón de carecer de comunicación motriz entre dos de sus equipos, no
obstante se puede jugar bajo esta situación si las fuerzas de los equipos
siguen una distribución reequilibradora.
Otro aspecto de interés lo encontramos
en la práctica de un juego motor ambivalente de tríada, donde puede que no
apreciemos coaliciones entre los jugadores, lo que nos hace pensar en su
vínculo con la comprensión y el aprendizaje, y en la rapidez de las acciones
motrices las cuales dificultan la asimilación estratégica. Estas cuestiones se
hacen evidentes al observar una supuesta conducta ambivalente y discernir si se
trata de una acción intencionada. Todo esto no debe verse como una pérdida de
personalidad de la tríada, sino como una parte del fenómeno que encierra.
Tras la perspectiva interna de la
tríada, dirigimos la mirada a la pedagogía de la educación física, donde llama la atención la escasez de construcción
teórica y soluciones prácticas que se aplican con relación a los juegos motores
de tríada. Y más, cuando podría haber cuestiones con alto interés pedagógico,
como la asimilación social de la ambivalencia y su posibilidad de interacciones
grupales.
En definitiva, las fórmulas de juegos derivadas
de la tríada motriz requieren ser examinadas en profundidad y con enfoque
educativo. Nos proponemos, entonces: a) identificar las distintos tipos a que
da lugar la tríada motriz; b) reconocer y medir qué aspectos marcan las
diferencias entre ellos en las tríadas estudiadas; y c) mostrar con juegos
concretos la viabilidad de los juegos de tríada para enriquecer los programas
de juegos motores en la educación física.
2.
MÉTODO
Se
sigue un estudio descriptivo, a través de un método comparativo de casos,
sustentado en la praxiología motriz (Parlebas, 1976, 1981, 1988, 2001) sobre
cuatro juegos motores de tríada, a partir de las redes de comunicación motriz, de
los flujos de comunicación, y de las emisiones y recepciones de los flujos de
comunicación enmarcadas en los valores intragrupo e intergrupos (Parlebas, 1981,
p.299-301); para ello, se toman los roles como etiquetas agregadas al flujo
(Parlebas, 1981, p.193,197; Wasserman y Faust, 2013, p.366).
2.1. Los juegos seleccionados
Se seleccionaron cuatro juegos motores
de tríada (tres de persecución y uno de captura mediante pelotas): ‘laberinto’
(adaptado de Navarro, 1995), ‘pelota aliada’, ‘encadenados’ y ‘vente conmigo’. Los
juegos se corresponden con los tipos 1 (‘laberinto’, ‘pelota aliada’) y 6 (‘vente
conmigo’), ambos con todos sus vértices conectados; y, por su parte, con la
forma el tipo 8 (‘encadenados’), carente de una conexión entre dos de sus
vértices. Se han incluido dos versiones del tipo 1, porque en una de ellas (‘pelota
aliada’) se establece la regulación de la situación de alianza. Los cuatro
juegos motores que se comparan son juegos motores diseñados y puestos en práctica
con alumnado de educación secundaria, y corresponden a tres redes de
comunicación motriz.
En el juego ‘laberinto’ (tipo 1,
figura 1), la rivalidad es compartida por los tres equipos (A↔B, A↔C, B↔C),
conformando así una estructura equilibrada (Heider, 1946) de soluciones
motrices; el rol ‘capturador’ realiza capturas sobre el ‘esquivador’ que huye,
pero también puede ocurrir que lo haga sobre otro capturador adversario a modo
de encuentro, ya que la acción de captura requiere un contacto difícil sobre el
cuerpo del oponente y esto reorganiza la estrategia de encuentros recíprocos
(Navarro, 1995, 2006, p.98); por su parte, el jugador ‘prisionero’ espera ser
liberado por el jugador ‘salvador’, lo cual favorece el componente cooperativo
entre los compañeros. La singularidad de este juego es que, mediante una regla
de limitación del contacto, según un criterio de intensificación de la dificultad,
los jugadores libres adversarios pueden elegir ser ‘capturador’ o ‘esquivador’,
según las circunstancias estratégicas, lo que supone una diversificación del
rol antagonista.
El juego ‘pelota aliada’ comparte tipo
de tríada con el juego laberinto
(tipo 1, figura 1), pero con la singularidad de que la acción de alianza está
regulada por una condición. Presenta cinco roles simétricamente compartidos por
los tres equipos que participan en el juego (‘lanzador’, ‘esquivador’,
‘prisionero’, ‘lanzador en alianza’, ‘salvador’), y el desarrollo estratégico
se genera a partir de las tres pelotas de distinto color que capacitan para dos
emisiones negativas de lanzamiento y una positiva de salvar.
El juego ‘encadenados’
corresponde a una comunicación en la que dos nodos están conectados y uno carece de conexión (tipo
8, figura 1), al contrario que el resto
de los juegos estudiados. Los tres equipos poseen cinco roles, los cuales no
son simétricos entre sí. Al ser esta una tríada carente de una conexión,
aparentemente se muestra como un doble enfrentamiento (A↔B, A↔C), con una vulnerabilidad mayor en el
equipo A; la viabilidad como juego motor se resuelve compensando las opciones
estratégicas del equipo en desventaja. En
este juego, los roles ‘capitán’ y ‘encadenado’ son exclusivos de los equipos B
y C, mientras que los roles exclusivos del bando A son ‘jugador libre’ y
‘recolector’. Por tanto el único rol compartido por los tres equipos sería el
rol ‘capturador’.
El juego ‘vente conmigo’ corresponde a una tríada conectada en todos sus
vértices, pero con asimetría de fuerzas (tipo 6, figura 1). De este modo los equipos A y B tienen equilibrio en su
flujo de comunicación bidireccional A↔B frente a C, que
solamente recibe emisiones negativas de los otros equipos (A→C, B→C). La viabilidad del juego se hace posible al compensar el
desequilibrio con opciones exclusivas de rol para el equipo C. El equipo A posee dos roles (‘capturador’ y ‘esquivador’) al igual que el
equipo B, mientras C dispone de los roles ‘esquivador’, ‘prisionero’ y
‘salvador’. Este último rol y la diferencia en el número de jugadores a favor
de C permite compensar la actuación del rol ‘capturador’, que es privilegio de
A y B.
2.2.
Procedimiento
Para responder a nuestro primer
objetivo (identificar las distintas formas de tríadas), comparamos los tipos de
redes de comunicación motriz de Parlebas (1988, p.212-215), y tendremos en
cuenta el planteamiento de Caplow (1968, p.57) para la interpretación de las
diferencias de poder y el sentido que tiene en el diseño de un juego.
Los cuatro juegos estudiados se
reparten entre las redes de comunicación motriz (Parlebas, 1988, p.215) del
siguiente modo: ‘laberinto’ y ‘pelota aliada’ (red ambivalente, estable), ‘encadenados’
(red exclusiva, inestable y permutante); y ‘vente conmigo’ (red ambivalente,
inestable y permutante). Por su parte, el análisis de Caplow (1956, 1959/1968)
partía de una diferencia de poder inicial, centrando la importancia en el
tamaño de los nodos o vértices. Sin embargo, partiremos de los flujos de
comunicación con el fin de abordar las diferencias de fuerzas, y no al revés,
porque esto es lo que explica mejor el modelo desde las condiciones de la
acción motriz.
Si tomamos como criterios el flujo de
comunicación y su dirección, se encuentran 64 casos posibles de tríadas (26)
(Holland y Leinhardt, 1974; Wasserman, 1975, p.5; Wasserman y Faust, 2013, p.583;
Moody, 1998, p.292; Batagelj y Mrvar, 2000, p.2). De ellos, 16 casos son
tríadas originales, no repetidas. Una vez eliminadas las versiones equivalentes
que pueden darse al combinar tres elementos, encontramos 13 tipos que
consideramos viables de ser jugadas como juegos motores, de las cuales 7 tienen
flujos dirigidos (tres nodos conectados), y 6 poseen ausencia de una conexión (figura
1):
Fig. 1. Tipos de tríadas propuestas
a partir de los censos de los autores anteriores. Tipos propuestos por los
autores, viables como juegos motores
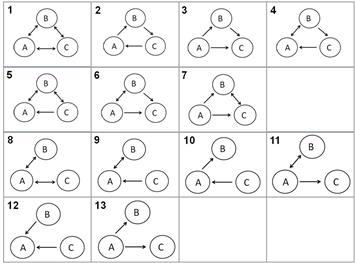
De todas estos tipos, solo son
conocidas como juegos motores las tríadas completas 1 (laberinto, Navarro, 1995,
2002), y 2 (‘zorros, gallinas y víboras’, o también conocido por ‘los tres
campos’) (Guillemard et al., 1988; Parlebas, 1988). Para los tipos del 8 al 13,
asumidos como diferencias de fuerzas (Caplow, 1956, 1959), son recogidos dentro
de la lógica interna que desarrolla el sistema de roles y subroles de Parlebas
(1981, p.193,197). Hemos aplicado un principio de reequilibrio al diseñar los
juegos de los tipos 8 y 6.
Para proceder a nuestro segundo
objetivo (reconocer qué aspectos marcan las diferencias entre los tipos
estudiados), el análisis comparativo de los cuatro juegos estudiados, se
realiza mediante cinco indicadores: roles, interacción intragrupo, interacción
intergrupos, emisiones o recepciones (flujos de comunicación), y valencia
positiva o negativa (Heider, 1946) (tablas 1-4). Los indicadores corresponden a
la estructura interna de comunicación, de forma que el rol es la referencia
social de las relaciones motrices, la interacción intragrupo muestra el grado
de relación entre los compañeros, y la interacción intergrupos señala el grado
de relación hacia los adversarios; ambas interacciones se muestran por medio de
emisiones y recepciones, que son entendidas como la valencia positiva
(solidaridad) o negativa (antagonismo) asociada, respectivamente.
Se comparan los cuatro juegos mediante
un cómputo que tiene en cuenta el vértice o nodo que representa cada equipo
(A,B,C) y sus correspondientes emisiones (positivas o negativas) y recepciones
(positivas o negativas) (tablas 1-4). Así, en un juego de persecución con
relaciones idénticas y tomando el vértice ‘A’ (equipo A) de la interacción
motriz ‘capturador-esquivador’, resultan dos emisiones negativas en la
interacción motriz de A↔B, que, al incorporar las otras dos emisiones
de A↔C, resultan un total
de dos emisiones negativas para este vértice. Al representar los tres vértices
o nodos, lo haremos así (2,2,2). Este procedimiento se repite para cada rol y
su relación de comunicación, intragrupo (en el seno de un equipo) e intergrupos
(respecto a un equipo adversario), y se muestran en las tablas
El último de
nuestros objetivos (mostrar la viabilidad de los juegos de tríada para
enriquecer los programas de juegos motores) es valorado paralelamente al
desarrollo del objetivo anterior, pues se sustenta en la jugabilidad de los tipos
de juegos comparados.
- COMPARATIVA DE JUEGOS. RESULTADOS
Al comparar los cuatro juegos motores estudiados,
siguiendo el procedimiento aludido, los resultados son los siguientes:
Tipo 1 (juego: laberinto, adaptado
de Navarro, 1995) (tabla 1): En una red de comunicación motriz ambivalente y estable,
las interacciones intragrupales frente a las intergrupales muestran un juego
centrado fuertemente en el antagonismo (36 interacciones intergrupos frente a 6
intragrupo:
Tabla 1. Interacciones en el juego ‘laberinto’ (tipo 1)
|
Tipo 1 |
Intragrupo |
Intergrupos |
|||||||
|
Emisiones |
Recepciones |
Emisiones |
Recepciones |
||||||
|
+ |
- |
+ |
- |
+ |
- |
+ |
- |
||
|
Juego |
Roles |
|
|
|
|
|
|
|
|
|
Laberinto |
Capturador |
0,0,0 |
0,0,0 |
0,0,0 |
0,0,0 |
0,0,0 |
6,6,6 |
0,0,0 |
2,2,2 |
|
Esquivador |
0,0,0 |
0,0,0 |
0,0,0 |
0,0,0 |
0,0,0 |
0,0,0 |
0,0,0 |
2,2,2 |
|
|
Prisionero |
0,0,0 |
0,0,0 |
1,1,1 |
0,0,0 |
0,0,0 |
0,0,0 |
0,0,0 |
0,0,0 |
|
|
|
1,1,1 |
0,0,0 |
0,0,0 |
0,0,0 |
0,0,0 |
0,0,0 |
0,0,0 |
2,2,2 |
|
|
Total |
1,1,1 |
0,0,0 |
1,1,1 |
0,0,0 |
0,0,0 |
6,6,6 |
0,0,0 |
6,6,6 |
|
|
|
6 interacciones intragrupo (6 positivas, 0 negativas) En total (A,B,C= 3 emisiones positivas y 3 recepciones
positivas) |
36 interacciones intergrupos (0 positivas y 36 negativas) En total (A,B,C= 18 emisiones negativas y 18
recepciones negativas) |
|||||||
|
Total: 42 interacciones
motrices (6 positivas y 36 negativas: |
|||||||||
Tipo 1 (juego: ‘pelota aliada’) (tabla
2): De nuevo, como en el juego ‘laberinto’, en una red de comunicación motriz
ambivalente y estable, las interacciones intragrupales frente a las
intergrupales muestran un juego centrado en el antagonismo, aunque en el caso
de pelota aliada es menos acusado (30
interacciones intergrupo frente a 6 intragrupo) en las interacciones de los
flujos entre los tres equipos. Las emisiones y las recepciones intergrupos se
ven incrementadas por la valencia positiva o cooperativa (12 positivas frente a
18 negativas). Las 12 emisiones-recepciones positivas intergrupos se concentran
en el rol lanzador coaligado,
mientras que todas las emisiones negativas intergrupos se distribuyen en tres
roles. A pesar de que se trata de un juego que comparte el mismo tipo que el juego
anterior, ahora este descentra el interés principal del antagonismo a favor de
la cooperación eventual, y se equilibran antagonismo y solidaridad en el total
de interacciones motrices (36) y se evidencia en términos relativos en la
proporción de
Tabla 2. Interacciones en el juego ‘pelota aliada’ (tipo 1)
|
Tipo 1 |
Intragrupo |
Intergrupos |
|||||||
|
Emisiones |
Recepciones |
Emisiones |
Recepciones |
||||||
|
+ |
- |
+ |
- |
+ |
- |
+ |
- |
||
|
Juego |
Roles |
|
|
|
|
|
|
|
|
|
Pelota aliada |
Lanzador (pelota roja) |
0,0,0 |
0,0,0 |
0,0,0 |
0,0,0 |
0,0,0 |
2,2,2 |
0,0,0 |
0,0,0 |
|
(pelota
verde) |
1,1,1 |
0,0,0 |
0,0,0 |
0,0,0 |
0,0,0 |
0,0,0 |
0,0,0 |
0,0,0 |
|
|
Lanzador
coaligado (pelota
blanca) |
0,0,0 |
0,0,0 |
0,0,0 |
0,0,0 |
2,2,2 |
1,1,1 |
2,2,2 |
0,0,0 |
|
|
Prisionero |
0,0,0 |
0,0,0 |
1,1,1 |
0,0,0 |
0,0,0 |
0,0,0 |
0,0,0 |
0,0,0 |
|
|
Esquivador |
0,0,0 |
0,0,0 |
0,0,0 |
0,0,0 |
0,0,0 |
0,0,0 |
0,0,0 |
3,3,3 |
|
|
Total |
1,1,1 |
0,0,0 |
1,1,1 |
0,0,0 |
2,2,2 |
3,3,3 |
2,2,2 |
3,3,3 |
|
|
|
6 interacciones
intragrupo (6 positivas, 0
negativas) En total (A,B,C= 3 emisiones positivas y 3 recepciones
positivas) |
30 interacciones
intergrupos (12 positivas y 18
negativas) En total (A,B,C= 12 emisiones positivas y 18
recepciones negativas) |
|||||||
|
Total: 36 interacciones motrices (18 positivas y
18 negativas: |
|||||||||
Tipo 8 (juego: ‘encadenados’)
(tabla 3): Se trata de un juego con una red ambivalente, inestable y permutante, que muestra que las
relaciones intragrupo son escasas (4 emisiones positivas), siendo un juego
marcadamente antagonista (0 positivas, 31 emisiones negativas), lo que
evidencia el doble enfrentamiento de B y C contra A en esta situación singular
en la que se impide por las reglas la comunicación entre B y C. La doble díada
trae consigo mayor antagonismo relativo (
Tabla 3. Interacciones en el juego ‘encadenados’ (tipo 8)
|
Tipo 8 |
Intragrupo |
Intergrupos |
|||||||
|
Emisiones |
Recepciones |
Emisiones |
Recepciones |
||||||
|
+ |
- |
+ |
- |
+ |
- |
+ |
- |
||
|
Juego |
Roles |
|
|
|
|
|
|
|
|
|
Encadenados |
Capitán |
0,0,0 |
0,0,0 |
0,1,1 |
0,0,0 |
0,0,0 |
0,3,3 |
0,0,0 |
0,1,1 |
|
Encadenado |
0,1,1 |
0,0,0 |
0,0,0 |
0,0,0 |
0,0,0 |
0,3,3 |
0,0,0 |
0,0,0 |
|
|
Jugador
libre |
0,0,0 |
0,0,0 |
0,0,0 |
0,0,0 |
0,0,0 |
0,0,0 |
0,0,0 |
4,0,0 |
|
|
Recolector |
0,0,0 |
0,0,0 |
0,0,0 |
0,0,0 |
0,0,0 |
0,0,0 |
0,0,0 |
4,0,0 |
|
|
Recuperador (gana
jugador) |
0,0,0 |
0,0,0 |
0,0,0 |
0,0,0 |
0,0,0 |
2,0,0 |
0,0,0 |
4,0,0 |
|
|
Total |
0,1,1 |
0,0,0 |
0,1,1 |
0,0,0 |
0,0,0 |
2,6,6 |
0,0,0 |
12,1,1 |
|
|
|
4 interacciones
intragrupo (4 positivas, 0
negativas) En total (A,B,C= 4 emisiones positivas y 0 recepciones
positivas) |
28 interacciones
intergrupos (0 positivas y 28
negativas) En total (A,B,C= 14 emisiones negativas y 14
recepciones negativas) |
|||||||
|
Total: 32 interacciones motrices (4 positivas y 28
negativas: |
|||||||||
Tipo 6 (juego: ‘vente conmigo’)
(tabla 4): Corresponde a una red ambivalente, inestable y permutante, y sus relaciones intragrupo son muy escasas (1
emisión positiva, 1 recepción positiva), menor que el juego encadenados; además, el desequilibrio
inicial de sus flujos de comunicación es muy reducido (8 emisiones negativas
intergrupos). Esto también se explica porque el equipo C compensa sus fuerzas
con acciones cooperativas (emisiones positivas intragrupo). Sin embargo, la
focalización de fuerzas de A y B contra C, y la circunstancia de enfrentamiento
recíproco entre A y B, acarrea una relación de
Tabla 4. Interacciones en el juego ‘vente conmigo’ (tipo 6)
|
Tipo 6 |
Intragrupo |
Intergrupos |
|||||||
|
Emisiones |
Recepciones |
Emisiones |
Recepciones |
||||||
|
+ |
- |
+ |
- |
+ |
- |
+ |
- |
||
|
Juego |
Roles |
|
|
|
|
|
|
|
|
|
Vente conmigo |
Capturador |
0,0,0 |
0,0,0 |
0,0,0 |
0,0,0 |
0,0,0 |
4,4,0 |
0,0,0 |
1,1,0 |
|
Esquivador |
0,0,0 |
0,0,0 |
0,0,0 |
0,0,0 |
0,0,0 |
0,0,0 |
0,0,0 |
1,1,2 |
|
|
|
0,0,1 |
0,0,0 |
0,0,0 |
0,0,0 |
0,0,0 |
0,0,0 |
0,0,0 |
0,0,2 |
|
|
Prisionero |
0,0,0 |
0,0,0 |
0,0,1 |
0,0,0 |
0,0,0 |
0,0,0 |
0,0,0 |
0,0,0 |
|
|
Total |
0,0,1 |
0,0,0 |
0,0,1 |
0,0,0 |
0,0,0 |
4,4,0 |
0,0,0 |
2,2,4 |
|
|
|
2 interacciones
intragrupo (2 positivas, 0 negativas) En total (A,B,C= 1 emisiones positivas y 1 recepciones
positivas) |
16 interacciones
intergrupos (0 positivas, 16 negativas) En total (A,B,C= 8 emisiones negativas y 8 recepciones
negativas) |
|||||||
|
Total: 18 interacciones motrices (2 positivas y 16
negativas: |
|||||||||
Los resultados comparados arrojan
diferencias entre los dos juegos del tipo 1 de las redes ambivalentes estables,
lo que señala variabilidad entre un mismo tipo de tríada. De este modo, el
juego ‘laberinto’ muestra un acusado
antagonismo, mientras que pelota aliada
descentra el antagonismo gracias a la cooperación eventual intergrupos, con
resultados más equilibrados que el primer juego. El juego ‘encadenados’ señala
un antagonismo más moderado que laberinto,
en términos absolutos, pero no de manera relativa, que es superior en el
primero. Y en el juego ‘vente conmigo’ encontramos un reducido antagonismo en
términos absolutos, con gran equilibrio entre emisiones y recepciones, positivas
y negativas, como producto de su red ambivalente inestable y permutante y del
desarrollo de la tarea; sin embargo, en términos relativos este juego es el de
rivalidad más intensa.
Finalmente, el balance entre la
rivalidad y la solidaridad (relación entre el total de interacciones motrices
positivas y el de las negativas) arroja que los dos juegos con simetría en sus
relaciones de flujos (‘laberinto’:
- DISCUSIÓN Y CONCLUSIONES
La
comunicación de tríada es singular, y difiere del modelo cultural de juegos más
frecuente, que es el juego de enfrentamiento dual; ello, la ha convertido en
una rareza lúdica, y la hace ausente en los programas de juegos. Nuestro
estudio muestra nuevas formas de comunicación de la tríada que son viables como
juegos motores, y pone al alcance conocer su comportamiento específico, así
como enriquecer el abanico de situaciones motrices que ofrecen los programas de
juegos.
A
través de la praxiología motriz hemos podido identificar, en los tipos de
tríadas estudiados, diferentes redes de comunicación, además de reafirmarse la validez
de los roles para entender el funcionamiento de la lógica interna de los
juegos. De este modo, centrados en los roles y en las emisiones y recepciones (+
o -) definidas en la acción de juego (Parlebas, 1981, p.285), hemos establecido
una comparativa reveladora en algunos de los tipos de tríadas descritos.
Además, se constata la relevancia del peso de la tarea (Flament, 1977),
derivada de la acción motriz, y cómo establece condiciones para esa
comunicación.
Hemos
comprobado en el análisis interno cómo los tipos de tríadas con carencia de una conexión entre dos de sus tres
elementos, son viables motrizmente. Los tipos
del 8 al 13 poseen el número de conexiones mínimo entre nodos para jugarse como
un verdadero juego motor; por consiguiente, situamos aquí el límite de
comunicación para el ‘agujero estructural’, al que se refería Burt (2004). De
este modo y para los juegos motores, se reduce el censo de tríadas de 16
(Wasserman, 1975) a 13.
Las
diferencias de ‘poder’ de los equipos, a las que aludía Caplow, hemos visto que pueden ser compensadas para el
grupo más débil con un nuevo rol, con más efectivos, o con nuevas opciones para
un rol ya establecido. Así, es posible jugar a determinadas tríadas, tal y como
hemos mostrado con los juegos ‘encadenados’ y ‘vente conmigo’. Coincidimos con
Parlebas (2011, p.23, 9) en su comentario a Caplow (1968), pues en los juegos
deportivos con tres equipos estos disponen, al menos, de dos opciones para escoger y, con cualquiera de estas
opciones, los tres equipos (o jugadores) habrían escogido una alternativa
diferente. En definitiva, compartimos con Elías (1995, p.88) que «(…) el efecto
de poder se ha sustituido por el de ‘fuerza relativa de juego’».
En
las tríadas motrices, son claras las tres versiones de las redes de
comunicación: solidaridad, rivalidad, y ambivalencia a las que se refirió Mills
(1953), resultándonos un concepto válido la ‘pugna frente a la dominancia’,
pues actúa como el impulsor estratégico de la coalianza. Esta propiedad de
coalianza la hemos materializado en la regla en el juego ‘pelota aliada’, y ha desvelado
un incremento de las interacciones de valencia positiva frente a las de
valencia negativa realizadas de manera consciente. En consecuencia, la
coalianza materializada en una regla asegura la voluntariedad de las acciones
ambivalentes de los jugadores. Al incluir esta condición en la regla, se evita
que su desarrollo se haga con estrategias más propias de una díada. En
definitiva, esta versión hace la paradoja tangible para los jugadores.
El
contexto en el que se da la alianza en las tríadas motrices se describe por las
rápidas acciones propias del comportamiento estratégico de los jugadores. Acciones
vertiginosas sobre situaciones donde las decisiones se dan en tiempos muy
cortos (Mahlo, 1969, p.84,120), y la mayoría de las veces alejadas de una
reflexión con garantías para el jugador. Esto nos hizo repensar la realidad de
la ambivalencia puesta en práctica, y nos condujo a diseñar el juego ‘pelota
aliada’; en este juego hemos
comprobado ventajas en definir la alianza en la reglas, y se consiguen dos
cosas: que los jugadores capten el sentido estratégico de la coalianza, y
evitar que haya juegos de tríada en los que los jugadores no son conscientes de
que algunas de sus acciones (involuntarias) resulten ser paradójicas.
No
podemos establecer el paralelismo entre el contexto motriz del juego de tríada con
el análisis matemático de los juegos, pues este último requeriría un proceso
reflexivo significativo para las decisiones de los jugadores. El análisis
matemático de las conductas humanas en acción, al que se refería Barbut (1967),
tiene en la tríada motriz un buen ejemplo. Las reglas de conducta (conductas) son
para Barbut (1967, p.841) las que ponen en relación los fines y los medios
(esquema de causalidad frente a esquema de finalidad), y ambos quedan descritos
en la lógica interna del juego motor.
Las
diferencias encontradas entre los tipos de tríadas estudiados nos indican una
diversificación del antagonismo, pero que se ha de examinar finalmente en
términos relativos. En un principio, los resultados totales de las emisiones
positivas y negativas en la interacción de las tríadas motrices examinadas ofrecen
un antagonismo mayor, en términos absolutos, cuando hay simetría entre los tres
equipos y se intensifica la interacción intergrupos (juego ‘laberinto’); o
bien, un antagonismo que se descentra gracias a la coalianza eventual (juego ‘pelota
aliada’); o también un antagonismo relativizador de fuerzas de doble
enfrentamiento (juego ‘encadenados’); o, por último, muestran una reducción del
antagonismo, al incorporar acciones cooperativas para el equipo con menor
fuerza inicial, en una situación de comunicación inestable (jugadores que pasan
de bando entre los dos equipos con más fuerza inicial) (juego ‘vente conmigo’).
Sin embargo, en términos relativos, las mayores diferencias a favor de la
rivalidad sobre la solidaridad han sido:
La
realidad práctica de los juegos motores de tríada encuentra en los centros
educativos un motivo pedagógico y curricular. El primer motivo incumbe a los
valores que transmite, puesto que la tríada ejemplifica una fórmula trasgresora
de la polarización rivalidad-solidaridad. Pedagógicamente, esta fórmula es
oportuna de reconducir en la enseñanza cuanto más acusada sea la hegemonía del
pensamiento dualista como modelo prevalente. Como la educación contiene procesos
reflexivos sobre los fenómenos y conceptos que se aprenden, y sobre las
vivencias prácticas y los procedimientos con los que resolver las situaciones
de juego, cobra gran interés modelos menos habituales de juegos con los que
ampliar el bagaje de la motricidad.
REFERENCIAS
BIBLIOGRÁFICAS
Barbut, M. (1967). Jeux et mathématiques. En Roger Caillois (dir). Jeux et Sports, Encyclopédie de la
Pléiade, XXIII. Paris: Gallimard, 826-864.
Batagelj, V. y Mrvar, A. (2000). A subcaudratic triad
census algoritm for large sparse networks with small máximum degree. Social networks, 23 (3), 237-243.
Bauman, Z. (2005). Modernidad y
ambivalencia. Barcelona: Anthropos.
Boudon, R. (1980). Efectos perversos y orden social. México: Premia.
Burt, R. S. (2004). Structural Holes and Good Ideas.
The American Journal of Sociology,
110 (2), 349-399. Recuperado de http://dex.doi.org/10.1086/421787
Caplow, T. (1956). A
theory of coalitions in the triad. American
sociological review, 21 (4), 489-493.
Caplow, T. (1959). Further development of a theory of
coalitions in the triad. The American
Journal of Sociology, LXIV, 5, University of Chicago.
Caplow, T. (1968). Dos contra uno: Teoría de coaliciones en las triadas. Madrid: Alianza.
Elías, N. (1995). Sociología fundamental. Madrid: Gedisa. Original de 1970.
Esteban, J. y Mayoral, L. (2011). Ethic and religious polarization and social conflict. Barcelona economics
working paper series, 528, Graduate school of economics, Barcelona.
Flament, Cl. (1977). Redes de
Comunicación y Estructuras de Grupo. Buenos Aires: Ediciones Nueva Visión.
Gamson, W. (1961). An experimental test of theory of
coalitions formation. American
Sociological Review, 26, 4, 565-573.
Granovetter, M. (1973). The strength of weak ties. American Journal of Sociology,
1360-1380.
Guillemard, G, Marchal, J.Cl., Parent, M., Parlebas, P.
y Schmitt, A. (1988). Las cuatro esquinas de los juegos. Lérida:
Agonos.
Heider, F. (1946). Attitudes and cognitive
organtitation. Journal of Pchycology,
21, 107-112.
Holland, P.W. y Leinhardt, S. (1974). The statistical analysis of local
structure in social net works. NBER
Working Paper, 44.
Jorg, A. Three sided football. Disponible en https://www.youtube.com/watch?v=EzbnKQKszm4
Kadushin, C. (2013). Comprender las
redes sociales: teorías, conceptos y hallazgos, vol. 11, Madrid: CIS.
Lévi-Strauss, Cl. (1997). El
pensamiento salvaje. Mexico: FCE. Original de 1962.
Mahlo, F. (1969). L’acte tactique en jeu. Paris: Vigot.
Mills, T. M. (1953), Power relations in three-person
groups. American Sociological Review,
18, 351-357.
Mills, T. M. (1954). The coalition pattern in
three-person groups. American
Sociological Association, American Sociological, 19, (6), 567-667.
Moody,
J. (1998). Matrix methods for calculating the triad census. Social Networks, 20, 291-299.
Navarro, V. Estudio de conductas infantiles en un juego de reglas.
Análisis de la estructura de juego, edad y género. Tesis doctoral. Universidad
de Las Palmas de Gran Canaria, 1995. Recuperado de http://hdl.handle.net/10553/2016
Navarro, V, (2002). El Afán de
Jugar. Teoría y práctica de los juegos motores. Barcelona: INDE.
Navarro, V. (2006). 40 años de propuestas de juegos motores en educación
física. Comparativa entre las propuestas tradicionales y modernas de libros manuales de juegos motores. Revista de Educación, 340, 787-808. http://www.revistaeducacion.mec.es/re340_28.html
Navarro, V. (2009). Investigaciones cuasi-experimentales acerca de
conductas lúdicas en juegos motores de reglas, en V. Navarro y C. Trigueros
(eds.) Investigación y juego motor en
España. Lleida: Servicio de Publicaciones Universitat de Lleida, 325-368.
Navarro, V. (2011). Aplicaciones pedagógicas del diseño de juegos motores
de reglas en educación física. Ágora,
13 (1), 15-34.
Parlebas, P. (1976). Activités physiques et éducation motrice, 4. EPS, dossiers 1967-1977.
Parlebas, P. (1981). Contribution à
un lexique commenté de l’action motrice. Paris: INSEP.
Parlebas, P. (1988), Elementos de
Sociología del Deporte. Málaga: Unisport.
Parlebas, P. (1996). Los universales de los juegos deportivos. Praxiología
Motriz, 0, 15-29.
Parlebas, P. (2001). Juegos, deporte y sociedad. Léxico de praxiologia motriz. Paidotribo:
Barcelona.
Parlebas, P. (2005a). Mathematisation elementaire de l’action dans les
jeux sportifs. Mathematiques et Sciences
Humaines, 170
(2), 95-117. http://msh.revues.org/2952
Parlebas, P. (2005b). Modélisation dans les jeux et les sports. Mathematiques et Sciences Humaines, 170 (2), 11-45. http://msh.revues.org/2968
Parlebas, P. (2005c). Mathematiques, jeux sportifs, sociologie. Mathematiques et Sciences Humaines, 170 (2), 5-9. http://msh.revues.org/2966
Parlebas, P. (2010). Modélisation mathematique, jeux sportifs et sciences
socials. Mathematiques et Sciences
Humaines, 191
(3), 33-50. http://msh.revues.org/11861
Parlebas, P. (2011). Trio maudit
ou triade féconde? Le cas du jeu «pierre-feuille-ciseaux. Math. Sci. Hum / Mathematics and
Social Sciences, 196 (4), 5-25. http://msh.revues.org/12107
Puig, N. y Heinemann, K. (1991). El deporte en la perspectiva del año
2000, Papers, 38, 123-141. Recuperado
de http://www.ddd.uab.es/pub/papers/02102862n38/02102862n38p123.pdf
Robles, F. (2000). La ambivalencia como categoría sociológica en Simmel. REIS, 89, 219-235. http://www.jstor.org/stable/40184231
Sánchez, R. (2000). Del duelo a la paradoja: una propuesta de enseñanza
de los juegos tradicionales infantiles
basada en la comunicación motriz. III Jornades
d’Intercanvi d’Experiències d’Educació Física. Valencia: CEFIRE, 173-189.
Simmel, G. (1950).The
sociology of George Simmel. En K. Wolff (ed). New York: The Free Press-Mcmillan
Publisher Company.
Wasserman, S. (1975). Random directed graph
distributions and the triad census in social networks. NBER Working Paper, 113.
Wasserman, S. y Faust, K. (2013). Análisis de redes sociales. Métodos y aplicaciones. Madrid, CIS.
Número
de citas totales / Total references: 46 (100%)
Número
de citas propias de la revista / Journal’s own references: 5 (11%)
Rev.int.med.cienc.act.fís.deporte - vol. 17 - número
67 - ISSN: 1577-0354