 Sánchez-Sixto, A.; Harrison,
A.J. y Floría, P. (2019) La
importancia de la profundidad del contramovimiento en el ciclo
estiramiento-acortamiento / Importance of Countermovement Depth in Stretching
and Shortening Cycle Analysis. Revista Internacional de Medicina y Ciencias de
la Actividad Física y el Deporte vol. 19 (73) pp. 33-44 Http://cdeporte.rediris.es/revista/revista73/artimportancia1003.htm
Sánchez-Sixto, A.; Harrison,
A.J. y Floría, P. (2019) La
importancia de la profundidad del contramovimiento en el ciclo
estiramiento-acortamiento / Importance of Countermovement Depth in Stretching
and Shortening Cycle Analysis. Revista Internacional de Medicina y Ciencias de
la Actividad Física y el Deporte vol. 19 (73) pp. 33-44 Http://cdeporte.rediris.es/revista/revista73/artimportancia1003.htm
DOI: http://doi.org/10.15366/rimcafd2019.73.003
ORIGINAL
LA IMPORTANCIA DE LA PROFUNDIDAD DEL
CONTRAMOVIMIENTO EN EL CICLO ESTIRAMIENTO-ACORTAMIENTO
IMPORTANCE OF
COUNTERMOVEMENT DEPTH IN STRETCHING AND SHORTENING CYCLE ANALYSIS
Sánchez-Sixto,
A.1; Harrison, A.J.2 y Floría, P.3
1 Doctorando en Ciencias
de la Actividad Física y el Deporte. Departamento de Deporte. Centro de
Estudios Universitarios Cardenal Spínola CEU. Bormujos (España) asanchezsixto@ceuandalucia.es
2 Doctor en Ciencias de
la Actividad Física y el Deporte. Physical
Education & Sport Sciences. University of Limerick. Limerick (Irlanda) Drew.Harrison@ul.ie
3 Doctor en Ciencias de la
Actividad Física y el Deporte. Departamento de Deporte e Informática.
Universidad Pablo de Olavide. Sevilla (España) pfloriam@upo.es
Código
UNESCO / UNESCO CODE: 2406.04 Biomecánica / Biomechanics
Clasificación
del Consejo de Europa / Council of Europe Classification: 3. Biomecánica del
deporte / Biomechanics of sport
Recibido 7 de abril de 2017 Received
April 7, 2017
Aceptado 11 de septiembre de
2017 Accepted September 11, 2017
RESUMEN
El objetivo de la presente investigación
fue determinar la influencia de las variables relacionadas con la aplicación de
fuerza y el desplazamiento del centro de masas en las diferencias en la altura
saltada entre el salto sin contramovimiento (SJ) y el salto con contramovimiento
(CMJ). Participaron veintiséis hombres, realizando tres SJ y tres CMJ con 90°
de flexión de rodilla. El desplazamiento del centro de masas y la fuerza media
durante la fase de propulsión fueron significativamente superiores en el CMJ en
comparación con el SJ, explicando el 75% de la diferencia entre los dos saltos
y teniendo un 30% más de influencia el desplazamiento del centro de masas. No
hubo diferencias en la fuerza máxima. Los resultados sugieren la necesidad de
examinar el desplazamiento del centro de masas para interpretar adecuadamente
las diferencias entre el SJ y el CMJ cuando el criterio establecido es 90° de
flexión de rodilla.
PALABRAS
CLAVE: Biomecánica;
Salto, Cinética, Cinemática
ABSTRACT
The aim of this investigation was to determine the influences of force
application related variables and center of mass displacement on jump height
differences between squat jump (SJ) and countermovement jump (CMJ). Twenty six
males performed three squat jumps and three countermovement jumps with a 90°
knee flexion. The center of mass displacement during the upward movement phase
and the average force were significantly greater in CMJ than in SJ. Both
variables explained 75% of the differences in the flight height, having 30%
more influence the center of mass displacement. There were no differences in
peak force. The results of this research suggest the need to examine the center
of mass displacement during SJ and CMJ when a 90°of knee flexion criteria is
established.
KEY WORDS: Biomechanics,
jump, Kinetics, Kinematics.
INTRODUCCIÓN
La
diferencia en la altura de salto, entre el salto sin contramovimiento (SJ) y el
salto con contramovimiento (CMJ), ha sido una variable ampliamente utilizada
por entrenadores e investigadores, para valorar el ciclo
estiramiento-acortamiento (Castagna y Castellini, 2013; Yang, Chou, Chen,
Shiang y Liu, en prensa). Generalmente, la altura de salto alcanzada en el CMJ
es superior a la del SJ y esta diferencia en el rendimiento se atribuye a la
capacidad del sistema neuromuscular para producir una mayor potencia y trabajo
tras el contramovimiento (Bobbert, Gerritsen, Litjens y Van Soest, 1996).
Debido a que el trabajo es el producto de la fuerza y el desplazamiento del
centro de masas, los investigadores han analizado la influencia que tienen
ambos parámetros en la altura del salto vertical (Kirby, McBride, Haines y
Dayne, 2011).
El
análisis de la fuerza ha sido utilizado de manera frecuente para examinar las
diferencias en el rendimiento del salto vertical (Cormie, McBride y McCaulley,
2009; Feltner, Bishop y Perez, 2004; González-Badillo y Marques, 2010; Kirby et
al., 2011; Nuzzo, McBride, Cormie y McCaulley, 2008). Algunas investigaciones
han mostrado que el pico de fuerza alcanzado durante el salto vertical tenía influencia
en la altura de salto conseguida (Cormie et al., 2009; González-Badillo y
Marques, 2010). Sin embargo, en otros estudios la relación entre la fuerza
máxima y la altura máxima de salto fue inexistente (Kirby et al., 2011; Salles,
Baltzopoulos y Rittweger, 2011). Otras variables de fuerza, como la fuerza
media durante la fase de propulsión, han sido utilizadas para valorar el
rendimiento del salto vertical, observándose valores superiores de fuerza media
cuando la altura alcanzada en el salto era mayor (Feltner et al., 2004).
También, la fuerza en el instante en que comienza la fase de subida del
movimiento ha sido evaluada, mostrando un incremento en el trabajo durante esta
fase, que podría tener como consecuencia una mayor altura en el salto vertical.
El
rol del desplazamiento de masas durante el salto vertical también ha sido
ampliamente investigado en los últimos años (Kirby et al., 2011; Salles et al.,
2011). Un incremento en el desplazamiento del centro de masas durante la ejecución
del salto vertical podría incrementar el impulso neto durante la fase de
propulsión y, por tanto, incrementar la velocidad de despegue (Alexander, 1995;
Bobbert, Casius, Sijpkens y Jaspers, 2008; Samozino, Morin, Hintzy y Belli,
2010). Se ha demostrado que los deportistas entrenados tenían un mayor
desplazamiento del centro de masas durante la fase de subida del movimiento,
consiguiendo mayores alturas en el salto vertical que aquellos que no estaban
entrenados (Ugrinowitsch, Tricoli, Rodacki, Batista y Ricard, 2007). Debido al
conocimiento que existe referente a la influencia del desplazamiento del centro
de masas, los entrenadores e investigadores controlan el ángulo de flexión de
rodilla durante los test de SJ y CMJ (Hébert-Losier, Jensen y Holmberg, 2014;
Lloyd, Oliver, Hughes y Williams, 2011). A pesar de ello, podrían existir
diferencias en el desplazamiento del centro de masas por la influencia de otros
segmentos, como por ejemplo, el tronco (Kopper, Ureczky y Tihanyi, 2012). Por este motivo, determinar si existen
diferencias en el desplazamiento del centro de masas entre el SJ y el CMJ es de
vital importancia para ayudar a comprender las posibles diferencias en la
altura alcanzada en estos dos saltos.
Cuando
los entrenadores y preparadores físicos estiman la función del ciclo
estiramiento acortamiento a través de la diferencia de la altura del salto
entre el SJ y el CMJ, diferentes parámetros relacionados con la aplicación de
fuerza y el desplazamiento del centro de masas pueden influir en el resultado
(Bobbert et al., 2008). Bajo nuestro conocimiento, no hay trabajos que hayan
evaluado el desplazamiento del centro de masas en el SJ y el CMJ, dado que el
criterio de 90° de flexión de rodilla se entiende que asegura un mismo
desplazamiento del centro de masas en ambos tipos de salto. Sin embargo, el
posible efecto de otros segmentos corporales podría modificar el recorrido
llevado a cabo por el centro de masas durante el salto vertical (Kopper et al.,
2012). Un análisis del SJ y el CMJ contemplando variables de fuerza y
desplazamiento podría ser de utilidad para entrenadores e investigadores a la
hora de avanzar en la comprensión de las diferencias entre ambos saltos. Por
este motivo, el objetivo de la presente investigación fue determinar la influencia
de las variables relacionadas con la aplicación de fuerza y el desplazamiento
del centro de masas en las diferencias en la altura saltada entre el SJ y el
CMJ.
MATERIAL
Y MÉTODO
PARTICIPANTES
Veintiséis
jugadores de deportes colectivos a nivel recreacional participaron en esta
investigación (edad: 20.62 ± 3.46 años, altura: 1.79 ± 0.06 m y peso: 74.60 ±
6.14 kg). Al menos en los 6 meses previos a la investigación, ninguno de los
participantes presentaba lesión musculo-esquelética. La presente investigación
contó con la aprobación del Comité de Ética de Investigación de la Universidad
y todos los participantes firmaron el consentimiento informado antes de la
participación den el estudio. Todos los datos recogidos durante el presente
estudio fueron anonimizados y guardados en bases de datos seguras y siguiendo
la ley de protección de datos.
PROCEDIMIENTO
Los
participantes tuvieron que realizar saltos sin contramovimiento y con
contramovimiento sobre una plataforma de fuerzas (Quattro Jump, Kistler
Instrument AG, Winterthur, Switzerland), registrando a una frecuencia de 500
Hz. Antes del test, todos los participantes realizaron un calentamiento de 10
minutos que consistía en: 2 minutos de carrera a baja intensidad, estiramientos
dinámico y una serie de 6 saltos submáximos (Vetter, 2007). No se realizó una
sesión previa de familiarización debido a que todos los participantes eran
físicamente activos y en sus entrenamientos realizaban actividad que incluían tanto
SJ como CMJ. Por este motivo los 6 saltos del calentamiento, realizados sobre
la plataforma de fuerzas, fueron suficientes para asegurar la correcta
ejecución durante el test. Tras el calentamiento, los participantes realizaron
3 SJ y 3 CMJ de forma aleatorizada. Las instrucciones a los participantes
fueron estandarizadas y se resaltó la importancia de saltar lo más alto
posible. Los participantes mantuvieron los brazos en jarra, con las manos en la
cadera, desde el inicio del movimiento hasta la caída. También, se controló que
los pies se mantuvieran en el suelo durante todo el contramovimiento. Para el
test del SJ, los participantes flexionaban sus rodillas lentamente hasta
alcanzar una posición de 90°. En esta posición tenían que mantenerse durante 2 segundos
antes de la realización del salto y evitando que existiera contramovimiento
alguno. Para el CMJ, los participantes comenzaban de pie, realizaban un
contramovimiento en el que alcanzasen una flexión de rodilla de 90° e
inmediatamente realizaban la fase de propulsión tratando de alcanzar la mayor
altura posible (Hébert-Losier et al., 2014; Lloyd et al., 2011). Todos los
saltos fueron controlados por dos investigadores. Cuando alguna de las
indicaciones no eran realizadas de forma correcta, el salto era repetido. Un
total de 3 saltos exitosos de cada tipo fueron registrados, dando un tiempo de
descanso entre salto y salto de 2 minutos.
ANÁLISIS
El
salto con el que se consiguió mayor altura de cada tipo fue seleccionado para
realizar el análisis. El software de la plataforma de fuerzas (QuattroJump,
Type 2822A1-1, Version 1.0.9.2) fue utilizado para obtener los valores de
fuerza. La máxima altura del salto fue calculado a través del método del
impulso (Linthorne, 2001). El impulso neto fue obtenido integrando la fuerza
neta vertical con respecto al tiempo desde 2 segundos antes del primer
movimiento del participante (Street, McMillan, Board, Rasmussen y Heneghan,
2001), utilizando el método trapezoidal (Kibele, 1998). La velocidad del centro de masas fue
calculada dividiendo el impulso neto entre la masa del participante. El
desplazamiento del centro de masas fue obtenido a través de la velocidad del
centro de masas. Por último, el trabajo fue calculado con el producto de la
fuerza y el desplazamiento del centro de masas durante la fase de propulsión
(Street et al., 2001). Para poder excluir la influencia del peso en los
resultados, todas las variables de fuerza fueron normalizadas al peso corporal
(BW).
Varias
variables de rendimiento fueron determinadas durante la fase de propulsión del
salto vertical, que fue definida desde el instante de velocidad cero del centro
de masas hasta el instante de despegue. El instante de despegue fue definido
como la primera intersección de las fuerzas de reacción verticales con un
umbral. Este umbral fue establecido como la máxima diferencia entre el valor
registrado y el valor promedio de los registros obtenidos durante la fase de
vuelo (Street et al., 2001).
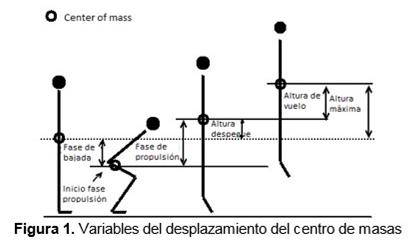
La
máxima altura, la altura de vuelo, la altura de despegue y la profundidad del
movimiento fueron identificadas a través de los datos de desplazamiento del
centro de masas (Figura 1). El desplazamiento del centro de masas durante la
fase de propulsión fue calculado desde el instante de inicio de la fase de subida
hasta el instante de despegue. El pico de fuerza fue el valor de fuerza más
alto alcanzado durante la fase de propulsión del movimiento. La fuerza media
fue calculada durante la fase de propulsión del salto. La fuerza al inicio de
la fase de propulsión fue el valor de fuerza encontrado en el instante en el
que el participante se encontraba en el punto más bajo del contramovimiento.
ANÁLISIS ESTADÍSTICO
El
análisis estadístico fue realizado con el software SPSS 18.0. Se calculó la
media y desviación estándar de todos los participantes en cada una de las
variables analizadas. Se verificó la normalidad de los datos a través del test
de Shapiro-Wilk. Cuando los datos seguían una distribución normal, una prueba T
para muestras relacionadas era utilizada para conocer las diferencias en las
variables entre el SJ y el CMJ. Cuando los datos no seguían una distribución
normal, el test no paramétrico de Wilcoxon era utilizado. El valor de
significación fue fijado a: P <
0,05. La magnitud de las diferencias entre las distintas variables de los
saltos fue calculada a través del tamaño del efecto de Cohen´s dz.
El criterio para interpretar la magnitud del cambio fue el siguiente: trivial =
0,00 – 0,19, pequeño = 0,20 – 0,59, moderado = 0,60 – 1,20 y largo > 1,20
(Hopkins, Marshall, Batterham y Hanin, 2009).
Una
regresión múltiple hacia atrás fue utilizada para determinar que parámetros
predecían de forma significativa las diferencias entre el SJ y el CMJ. Las
variables independientes fueron: la diferencia en el desplazamiento del centro
de masas entre el SJ y el CMJ, la diferencia en el pico de fuerza entre el SJ y
el CMJ y la diferencia en la fuerza media durante la fase de propulsión en
ambos saltos. La variable dependiente fue la diferencia en la altura de salto
alcanzada entre el SJ y el CMJ. Por último, los coeficientes beta
estandarizados fueron utilizados como estimador de la influencia de cada una de
las variables independientes sobre la variables dependiente.
RESULTADOS
Las
medias y desviaciones estándar (media ± SD) para cada variable durante el SJ y
el CMJ se presentan en la Tabla 1. Los resultados mostraron que el rendimiento
en la altura saltada fue un 15% superior en el CMJ con respecto al SJ y que
tuvo un tamaño del efecto moderado. No se encontraron diferencias en la altura
de despegue entre ambos tipos de saltos, pero si se encontraron diferencias
estadísticamente significativas y con un tamaño del efecto largo entre la
altura de vuelo, siendo mayor en el CMJ. Se encontraron diferencias en las
variables relacionadas con el desplazamiento del centro de masas entre los dos
saltos medidos. Los resultados mostraron que la profundidad que tenía el centro
de masas en el CMJ era superior a la que se alcanzaba en el SJ, siendo mayor la
distancia recorrida por el centro de masas durante la fase de propulsión del
movimiento. En las variables de aplicación de fuerza, se encontraron
diferencias estadísticamente significativas en la fuerza media, siendo mayor
para el CMJ en comparación el SJ y mostrando un tamaño del efecto pequeño. Sin
embargo, no se encontraron diferencias en el pico de fuerza alcanzado entre los
dos tipos de salto.
Tabla 1. Resultados (media ± SD) de las variables fase
propulsiva.
|
Variables
|
SJ |
CMJ |
Tamaño de efecto |
|
hmax
(m) |
0,41 ± 0,07 |
0,47 ± 0,06* |
0,85 |
|
Hvuelo
(m) |
0,28 ± 0,05 |
0,33 ±
0,05* |
1,29 |
|
Hdespegue
(m) |
0,13 ± 0,04 |
0,14 ± 0,03 |
0,12 |
|
W
(J·kg-1) |
2,93 ± 0,50 |
3,41 ± 0,55* |
1,27 |
|
Fmedia
(BW) |
1,95 ± 0,21 |
2,05 ± 0,15* |
0,53 |
|
Finicial
(BW) |
1,00 ± 0,00 |
2,44 ± 0,22* |
6,64 |
|
Fmax
(BW) |
2,52 ± 0,24 |
2,52 ±
0,20 |
-0,01 |
|
Dpropulsión
(m) |
0,35 ± 0,05 |
0,42 ± 0,03* |
1,55 |
|
Dprofundidad
(m) |
-0,22 ± 0,07 |
-0,28 ± 0,04* |
0,82 |
Nota: Hmax =
altura máxima, Hvuelo = altura de vuelo, Hdespegue =
altura de despegue, W = trabajo, Fmedia = fuerza media, Finicial
= fuerza en el instante de inicio de la fase de propulsión, Fmax =
fuerza máxima, Dpropulsión = desplazamiento del centro de masas
durante la fase de propulsión, Dprofundidad = posición del centro de
masas en el instante de inicio de la fase de propulsión.
*P < 0,05.
Los
resultados del análisis de regresión múltiple mostraron una relación fuerte entre
la diferencia en la altura de vuelo entre el SJ y el CMJ y las diferencias
entre el desplazamiento del centro de masas y la fuerza media entre ambos tipos
de salto (Tabla 2). Las diferencias en la atura de vuelo mostraron estar
asociadas a una mayor distancia de propulsión (P < 0.001) y una mayor fuerza media (P < 0,001) en el CMJ. Estas dos variables explican un 75% de la
varianza (Figura 2). De estas dos variables, la diferencia en el desplazamiento
del centro de masas durante la fase de subida del salto, entre el CMJ y el SJ,
tuvo una mayor influencia que la fuerza media (un 30% menor) a la hora de
explicar las diferencias en la altura de vuelo entre los dos tipos de
salto.
Tabla 2. Regresión múltiple para predecir la influencia
de las variables de desplazamiento y aplicación de fuerza sobre los cambios en
la altura de vuelo entre el SJ y el CMJ.
|
|
Coeficientes no estandarizados |
|
|
|
|
Variables independientes |
B |
Error estándar |
Coeficientes Beta estandarizados |
Valor-t |
|
R2 = 0,745, F = 33,96* |
|
|
|
|
|
(Constant) |
-0,019 |
0,009 |
|
-2,083 |
|
ΔDpropulsión |
0,795 |
0,103 |
0,901 |
7,750* |
|
ΔFmedia |
0,146 |
0,024 |
0,702 |
5,943* |
ΔDpropulsión:
diferencias entre el desplazamiento durante la fase de propulsión entre el SJ y
el CMJ. ΔFmedia: diferencias en la fuerza media entre el SJ y
el CMJ. *indica P<0,01
Predicción de la diferencia en Hvuelo (m)
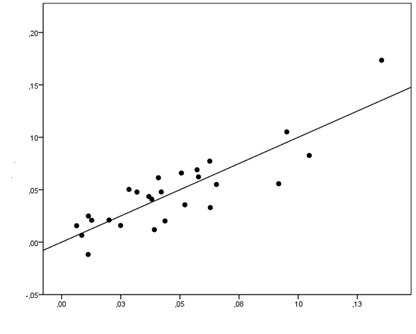
Figura 2. Diagrama de dispersión de la relación entre la diferencia
real y la esperada entre el SJ y el CMJ en la altura de vuelo (Hvuelo).
DISCUSIÓN
El objetivo de esta investigación fue
determinar la influencia de las variables relacionadas con la aplicación de
fuerza y con el desplazamiento del centro de masas en los cambios que se
producen en la altura de salto entre el SJ y el CMJ. El incremento en la altura
de vuelo entre el SJ y el CMJ quedó explicado en un 75% por las diferencias
entre el recorrido realizado por el centro de masas y las diferencias en la
fuerza media durante la fase de propulsión del movimiento. Debido a que la
altura de despegue no mostró diferencias entre los dos saltos realizados, las
diferencias en el desplazamiento del centro de masas durante la fase de
propulsión tuvieron que ser debidas a la mayor profundidad alcanzada durante el
CMJ. Estos resultados están en consonancia con previas investigaciones en las
que se encontró que el rendimiento del salto vertical se veía incrementado
cuando se producía un mayor desplazamiento en el centro de masas durante la
fase de propulsión (Kirby et al., 2011; Salles et al., 2011). En el presente
trabajo, las diferencias en el desplazamiento del centro de masas fueron
menores que en estos estudios previos, algo de esperar, ya que a la hora de evaluar
la función del ciclo estiramiento-acortamiento, se pretende que no existan
diferencias controlando el ángulo de flexión de rodilla. Sin embargo, a pesar
de la pequeña diferencia en la profundidad del movimiento acontecida entre el
SJ y el CMJ, el efecto producido fue el mayor determinante a la hora de
explicar la diferencia entre los dos saltos. Por este motivo, podemos observar
como no es necesario generar grandes cambios en el desplazamiento del centro de
masas para modificar el rendimiento del salto vertical (Sánchez-Sixto, Harrison
y Floría, 2016). Investigaciones previas encontraron una relación
estadísticamente significativa entre la altura de salto y el recorrido
realizado por el centro de masas (Barker, Harry, & Mercer, 2017). Ello
sugiere la necesidad de controlar el desplazamiento del centro de masas, a la
hora de evaluar la efectividad del ciclo estiramiento-acortamiento a través de
la diferencia saltada entre el SJ y el CMJ. Entrenadores, preparadores físico y
previas investigaciones, han utilizado, al igual que en la presente
investigación, el criterio estandarizado de 90° de flexión de rodilla en el SJ
y en el CMJ (Hébert-Losier et al., 2014;
Lloyd et al., 2011). Sin embargo, tras lo analizado en el presente trabajo,
este criterio es insuficiente para garantizar que el desplazamiento del centro
de masas no afecta a las diferencias encontradas entre los dos saltos
analizados. Una posible explicación es la relevancia que tienen otros
segmentos, de una mayor masa, como el tronco, en el desplazamiento del centro
de masas durante el salto vertical (Kopper et al., 2012). Por estos motivos,
parece necesario buscar nuevos métodos y protocolos que aseguren la
reproducibilidad de evaluar la efectividad del ciclo estiramiento-acortamiento
a través de la diferencia entre el SJ y el CMJ.
La
fuerza media durante la fase de propulsión del movimiento mostró diferencias
significativas entre el SJ y el CMJ, siendo la única variable de aplicación de
fuerza que mostró diferencias entre los dos tipos de salto. En investigaciones
previas, no mostró ser un buen predictor de la altura de salto (Barker et al.,
2017). No obstante, las condiciones de la presente investigación fueron
distintas, ya que el rango de movimiento en la investigación previa, fue muy
inferior y, se ha comprobado previamente, que el rango de movimiento influencia
este parámetro (Kirby et al., 2011; Salles et al., 2011). Por otro lado, otras
investigaciones han mostrado a la fuerza media como un factor determinante en
el rendimiento del salto vertical (Feltner et al., 2004). Debido a que el valor
medio de la fuerza es el resultado de un mayor número de puntos a lo largo del
salto vertical, la utilización de esta variable podría dar una información más
completa y representativa que otras variables instantáneas. El pico de fuerza
es la variable que más se ha medido en el salto vertical (Cormie et al., 2009;
Kirby et al., 2011; Nuzzo et al., 2008; Salles et al., 2011). Los datos del
pico de fuerza en la presente investigación, no mostraron diferencias entre el
SJ y el CMJ, a pesar de que el rendimiento en el segundo fue superior. Estos
resultados están en la línea de previas investigaciones en las que no se
encontró relación entre el pico de fuerza y el rendimiento en el salto vertical
(Kirby et al., 2011; Nuzzo et al., 2008). Un posible explicación es la relación
que parece tener el desplazamiento del centro de masas con el pico de fuerza,
donde se han observado que cuando se incrementa la profundidad del movimiento
disminuyen los valores del pico de fuerza (Kirby et al., 2011; Markovic,
Mirkov, Knezevic y Jaric, 2013; Salles et al., 2011). Por este motivo, el pico
de fuerza no parece una variable que determine el salto vertical cuando el
desplazamiento del centro de masas no es el mismo, como ocurrió en la presente
investigación al comparar el SJ y el CMJ. La fuerza conseguida en el instante
de inicio de la fase de subida del movimiento mostró diferencias entre ambos
saltos como es de esperar al comparar estos dos saltos. La fuerza en el SJ,
debe ser proporcional a su peso, de lo contrario habría existido un
contramovimiento previo a la acción de subida. Mientras, en el CMJ, debido a la
acción, de frenar la velocidad negativa del centro de masas durante el
contramovimiento, el valor de fuerza ha de ser superior al peso corporal. La
fuerza en el instante de transición excéntrico-concéntrico del movimiento en el
salto vertical ha sido descrita como un factor importante a la hora de
determinar las diferencias entre el SJ y el CMJ (Bobbert et al., 1996). Una mayor
fuerza en la transición podría dar lugar un incremento en el impulso neto
generado y traer como consecuencia un aumento de la velocidad de despegue del
centro de masas (Kirby et al., 2011). Sin embargo, en la presente
investigación, aquellos participantes que comenzaron un valor de fuerza inicial
superior, no necesariamente eran aquellos que alcanzaban la mayor altura en el
salto. Un estudio reciente mostró similares resultados, al no encontrar
relación entre la fuerza inicial y la altura alcanzada en el salto (Barker et
al., 2017). Futuros estudios deberían examinar el rol de la fuerza, en el
instante de inicio de la fase de propulsión del salto vertical, controlando el
desplazamiento del centro de masas; ya que este, podría ser relevante para para
su compresión en el rendimiento del salto vertical.
CONCLUSIÓN
La
presente investigación pone de manifiesto la importancia que tiene el control
del desplazamiento del centro de masas a la hora de evaluar la altura alcanzada
en el SJ y en el CMJ. El criterio de 90° de flexión de rodilla fue insuficiente
para garantizar que el desplazamiento del centro de masas fuera el mismo en los
dos tipos de salto. La influencia del recorrido del centro de masas fue la
variable que más explicó la diferencia entre la altura entre el SJ y el CMJ.
Por este motivo, parece fundamental el control de esta variable para evaluar el
ciclo estiramiento-acortamiento a través de la diferencia en la altura saltada
entre el SJ y el CMJ. Por último, el pico de fuerza y la fuerza al inicio del
movimiento de la fase de subida no fueron buenos predictores del rendimiento en
los saltos medidos, siendo la fuerza media la variable que más explicó la
ganancia en altura del CMJ frente al SJ.
REFERENCIAS
BIBLIOGRÁFICAS
Alexander,
R. M. (1995). Leg design and jumping technique for humans, other
vertebrates and insects. Philosophical
Transactions of the Royal Society of London B: Biological Sciences, 347,
235-248. doi: https://doi.org/10.1098/rstb.1995.0024.
Barker,
L. A., Harry, J. R., & Mercer, J. A. (en prensa). Relationships Between
Countermovement Jump Ground Reaction Forces and Jump Height, Reactive Strength
Index, and Jump Time. Journal of Strength & Conditioning Research.
Bobbert,
M. F., Casius, L. R., Sijpkens, I. W., & Jaspers, R. T. (2008). Humans
adjust control to initial squat depth in vertical squat jumping. Journal of
Applied Physiology, 105, 1428-1440. doi:
https://doi.org/10.1152/japplphysiol.90571.2008.
Bobbert,
M. F., Gerritsen, K. G., Litjens, M. C., & Van Soest, A. J. (1996). Why is
countermovement jump height greater than squat jump height? Medicine and
Science in Sports and Exercise, 28, 1402-1412. doi:
https://doi.org/10.1097/00005768-199611000-00009.
Castagna,
C., & Castellini, E. (2013). Vertical jump performance in Italian male and
female national team soccer players. Journal of Strength & Conditioning
Research, 27, 1156-1161. doi:
https://doi.org/10.1519/JSC.0b013e3182610999.
Cormie,
P., McBride, J. M., & McCaulley, G. O. (2009). Power-time, force-time, and
velocity-time curve analysis of the countermovement jump: impact of training.
Journal of Strength & Conditioning Research, 23, 177-186. doi: https://doi.org/10.1519/JSC.0b013e3181889324.
Feltner,
M. E., Bishop, E. J., & Perez, C. M. (2004). Segmental and kinetic
contributions in vertical jumps performed with and without an arm swing.
Research Quarterly for Exercise and Sport, 75, 216-230. doi:
https://doi.org/10.1080/02701367.2004.10609155.
González-Badillo, J. J., & Marques,
M. C. (2010). Relationship between kinematic factors and countermovement jump height
in trained track and field athletes. Journal of Strength and Conditioning
Research, 24, 3443-3447. doi:
https://doi.org/10.1519/JSC.0b013e3181bac37d.
Hébert-Losier,
K., Jensen, K., & Holmberg, H. C. (2014). Jumping and hopping in elite and
amateur orienteering athletes and correlations to sprinting and running.
International Journal of Sports Physiology and Performance, 9, 993-999. doi: https://doi.org/10.1123/ijspp.2013-0486.
Hopkins,
W., Marshall, S., Batterham, A., & Hanin, J. (2009). Progressive statistics
for studies in sports medicine and exercise science. Medicine and Science in
Sports and Exercise, 41, 3. doi:
https://doi.org/10.1249/MSS.0b013e31818cb278.
Kibele,
A. (1998). Possibilities and limitations in the biomechanical analysis of
countermovement jumps: A methodological study. Journal of Applied Biomechanics,
14, 105-117. doi: https://doi.org/10.1123/jab.14.1.105.
Kirby,
T. J., McBride, J. M., Haines, T. L., & Dayne, A. M. (2011). Relative net
vertical impulse determines jumping performance. Journal of Applied
Biomechanics, 27, 207-214. doi:
https://doi.org/10.1123/jab.27.3.207.
Kopper,
B., Ureczky, D., & Tihanyi, J. (2012). Trunk position influences joint
activation pattern and physical performance during vertical jumping. Acta
Physiologica Hungarica, 99, 194-205. doi:
https://doi.org/10.1556/APhysiol.99.2012.2.13.
Linthorne,
N. P. (2001). Analysis of standing vertical jumps using a force platform. American
Journal of Physics, 69, 1198-1204. doi:
https://doi.org/10.1119/1.1397460.
Lloyd,
R. S., Oliver, J. L., Hughes, M. G., & Williams, C. A. (2011). The
influence of chronological age on periods of accelerated adaptation of
stretch-shortening cycle performance in pre and postpubescent boys. Journal of
Strength and Conditioning Research, 25, 1889-1897. doi:
https://doi.org/10.1519/JSC.0b013e3181e7faa8.
Markovic,
S., Mirkov, D. M., Knezevic, O. M., & Jaric, S. (2013). Jump training with
different loads: effects on jumping performance and power output. European
Journal of Applied Physiology, 113, 2511-2521. Doi:
https://doi.org/10.1007/s00421-013-2688-6.
Nuzzo, J. L., McBride, J. M., Cormie,
P., & McCaulley, G. O. (2008). Relationship between countermovement jump performance
and multijoint isometric and dynamic tests of strength. Journal of Strength and
Conditioning Research, 22, 699-707. doi:
https://doi.org/10.1519/JSC.0b013e31816d5eda.
Salles, A. S., Baltzopoulos, V., &
Rittweger, J. (2011). Differential effects of countermovement magnitude and volitional effort
on vertical jumping. European Journal of Applied Physiology, 111, 441-448. doi: https://doi.org/10.1007/s00421-010-1665-6
Samozino,
P., Morin, J.-B., Hintzy, F., & Belli, A. (2010). Jumping ability: a
theoretical integrative approach. Journal of Theoretical Biology, 264, 11-18. doi: https://doi.org/10.1016/j.jtbi.2010.01.021.
Sánchez-Sixto,
A., Harrison, A., & Floría, P. (2016). Simple instructions on the crouch
position improve performance in the countermovement jump. 34 International
Conference on Biomechanics in Sports, 949-952.
Street,
G., McMillan, S., Board, W., Rasmussen, M., & Heneghan, J. M. (2001).
Sources of error in determining countermovement jump height with the impulse
method. Journal of Applied Biomechanics, 17, 43-54. doi:
https://doi.org/10.1123/jab.17.1.43.
Ugrinowitsch,
C., Tricoli, V., Rodacki, A. L., Batista, M., & Ricard, M. D. (2007).
Influence of training background on jumping height. Journal of Strength and
Conditioning Research, 21, 848-852.
Vetter,
R. E. (2007). Effects of six warm-up protocols on sprint and jump performance.
Journal of Strength and Conditioning Research, 21, 819-823.
Yang,
W. W., Chou, L. W., Chen, W. H., Shiang, T. Y., & Liu, C. (en prensa).
Dual-frequency whole body vibration enhances vertical jumping and
change-of-direction ability in rugby players. Journal of Sport and Health
Science.
Número
de citas totales / Total references: 24
(100%)
Número de citas propias de la revista /
Journal´s own references: 0 (0%)
Rev.int.med.cienc.act.fís.deporte
-
vol. 19 - número 73 - ISSN: 1577-0354